This post is based on an introduction talk that I gave at EAGxBerlin 2022. It is intended for policy researchers who want to extend their tool kit with computational tools. I show how we can support decision-making with simulation models of socio-technical systems while embracing uncertainties in a systematic manner. The technical field of decision-making under deep uncertainty offers a wide range of methods to account for various parametric and structural uncertainties while identifying robust policies in a situation where we want to optimize for multiple objectives simultaneously.
Summary
- Real-world political decision-making problems are complex, with disputed knowledge, differing problem perceptions, opposing stakeholders, and interactions between framing the problem and problem-solving.
- Modeling can help policy-makers to navigate these complexities.
- Traditional modeling is ill-suited for this purpose.
- Systems modeling is a better fit (e.g., agent-based models).
- Deep uncertainty is more common than one might think.
- Deep uncertainty makes expected-utility reasoning virtually useless.
- Decision-Making under Deep Uncertainty is a framework that can build upon systems modeling and overcome deep uncertainties.
- Explorative modeling > predictive modeling.
- Value diversity (aka multiple objectives) > single objectives.
- Focus on finding vulnerable scenarios and robust policy solutions.
- Good fit with the mitigation of GCRs, X-risks, and S-risks.
Complexity
Complexity science is an interdisciplinary field that seeks to understand complex systems and the emergent behaviors that arise from the interactions of their components. Complexity is often an obstacle to decision-making. So, we need to address it.
Ant Colonies
Ant colonies are a great example of how complex systems can emerge from simple individual behaviors. Ants follow very simplistic rules, such as depositing food, following pheromone trails, and communicating with each other through chemical signals. However, the collective behavior of the colony is highly sophisticated, with complex networks of pheromone trails guiding the movement of the entire colony toward food sources and the construction of intricate structures such as nests and tunnels. The behavior of the colony is also highly adaptive, with the ability to respond to changes in the environment, such as changes in the availability of food or the presence of predators.
Examples of Economy and Technology
Similarly, the world is also a highly complex system, with a vast array of interrelated factors and processes that interact with each other in intricate ways. These factors include the economy, technology, politics, culture, and the environment, among others. Each of these factors is highly complex in its own right, with multiple variables and feedback loops that contribute to the overall complexity of the system. For example, the economy is a highly complex system that involves the interactions between individuals, businesses, governments, and other entities. The behavior of each individual actor is highly variable and can be influenced by a range of factors, such as personal motivations, cultural norms, and environmental factors. These individual behaviors can then interact with each other in complex ways, leading to emergent phenomena such as market trends, economic growth, and financial crises. Similarly, technology is a highly complex system that involves interactions between multiple components, such as hardware, software, data, and networks. Each of these components is highly complex in its own right, with multiple feedback loops and interactions that contribute to the overall complexity of the system. The behavior of the system as a whole can then be highly unpredictable, with emergent phenomena such as network effects, disruptive innovations, and the potential for unintended consequences.
Socio-Technical Systems
In the context of EA, it might be particularly interesting to look at socio-technical systems. These are complex systems that involve the interactions between social and technical components, such as people, organizations, and technology. One key characteristic of these systems is non-linearity, which means that small changes or disruptions in one part of the system can have significant and unpredictable effects on other parts of the system. This non-linearity can contribute to the overall complexity of the system, making it difficult to understand and control. The non-linear and complex nature of socio-technical systems presents a significant challenge for policymakers. Policies and regulations designed to address specific issues or problems may have unintended consequences or fail to achieve their desired outcomes due to the complex interactions within the system. Additionally, policymakers may not have access to complete or accurate information about the system, making it difficult to make informed decisions. The multiple stakeholders involved in socio-technical systems may also have conflicting interests and goals, making it challenging to reach a consensus and implement effective policies. Furthermore, the rapid pace of technological change can exacerbate the complexity of these systems, as new technologies can disrupt established social and economic structures, creating new challenges for governance. To effectively address the complex challenges posed by socio-technical systems, policymakers need to adopt new approaches that embrace complexity and uncertainty, such as the methodology that I'm advocating in this post.

Modeling
We care about the state of the world. Policy-making can affect this state. However, navigating through a space of endless possibilities renders it hard to find good policy solutions to lead us to desirable world states. Intuition, or relying on personal experience and judgment, can be a useful tool in many situations, but it can also be unreliable and insufficient when it comes to understanding and acting on complex systems like the one described above. Ideally, we would like to see our policy-makers use evidence-based methods to support their decision-making process. Using formal modeling can be a way to offer such support.

What is Modeling?
But what is modeling actually? Modeling is the process of creating a simplified representation of a natural system that captures the key components, interactions, and behaviors of the system. This representation is encoded into a formal system, such as a computer program or mathematical equation, that can be used to simulate the behavior of the system under different conditions. Through the process of simulation, the formal system can be decoded back into a natural system, allowing policymakers and researchers to gain insights into the behavior and potential outcomes of the real-world system.
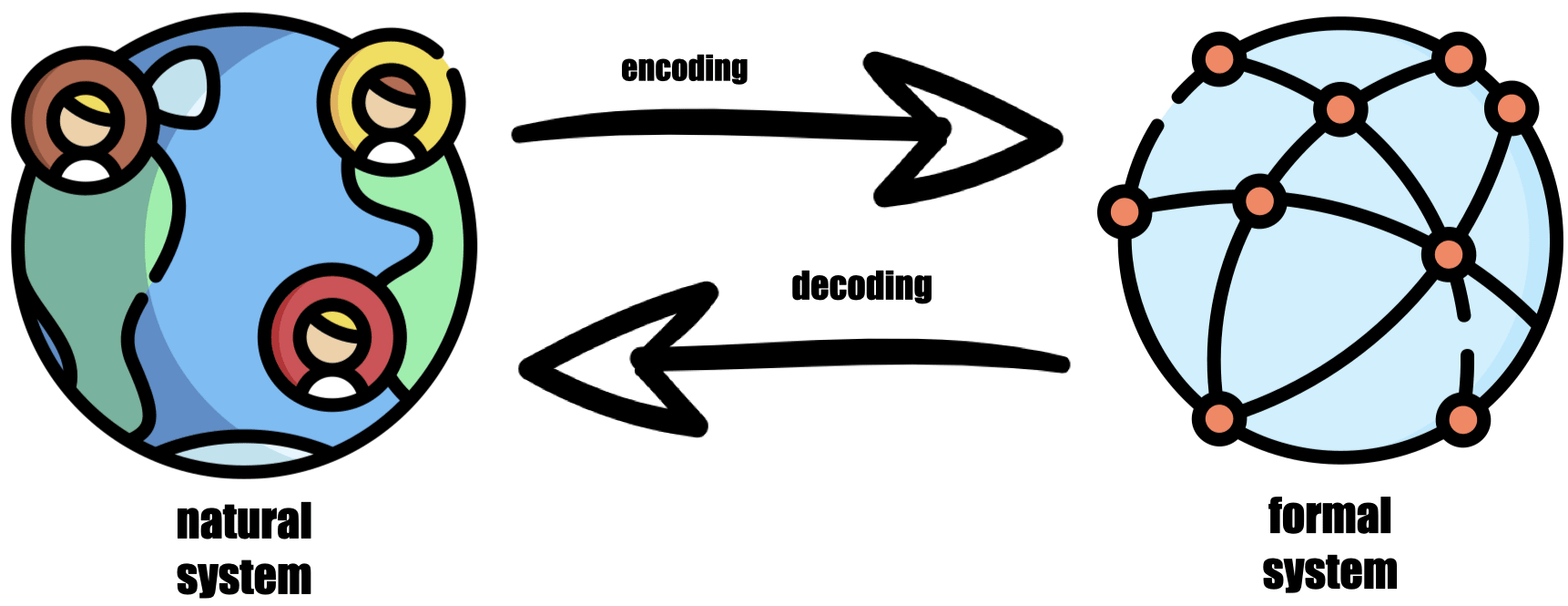
Why is Modeling Useful?
Modeling can be a powerful tool for understanding and managing complex systems, as it allows us to formalize our understanding of a system and explore different scenarios and outcomes. Formalization forces us to define and articulate our mental models of a system, which can expose any contradictory assumptions or gaps in our understanding. This process can help us identify areas where we need more data or research, or where our assumptions need to be revised. By formalizing our mental models and combining them with observed data, we can develop more accurate and comprehensive models of complex systems, which can be used to inform policy decisions and interventions.
Despite the gaps in our knowledge and the limitations of modeling, there is value in attempting to model complex systems. We cannot wait until we have perfect information to make policy decisions, as urgency often dictates that we must act even in the face of uncertainty. Modeling allows us to explore different scenarios and evaluate the potential outcomes of different policy options, even when we are uncertain about the behavior of the system.
As George Box famously said,
"All models are wrong, but some are useful."
While no model can perfectly capture the complexity and nuances of a real-world system, some models can still be useful in providing insights into the behavior of the system and potential outcomes of policy decisions. By embracing the imperfect nature of modeling and using it as a tool to refine and improve our understanding of complex systems, we can make more informed and effective policy decisions.
Traditional Modeling
I would like to distinguish two paradigms of modeling. Something that I call traditional modeling on the one hand, and systems modeling on the other hand.
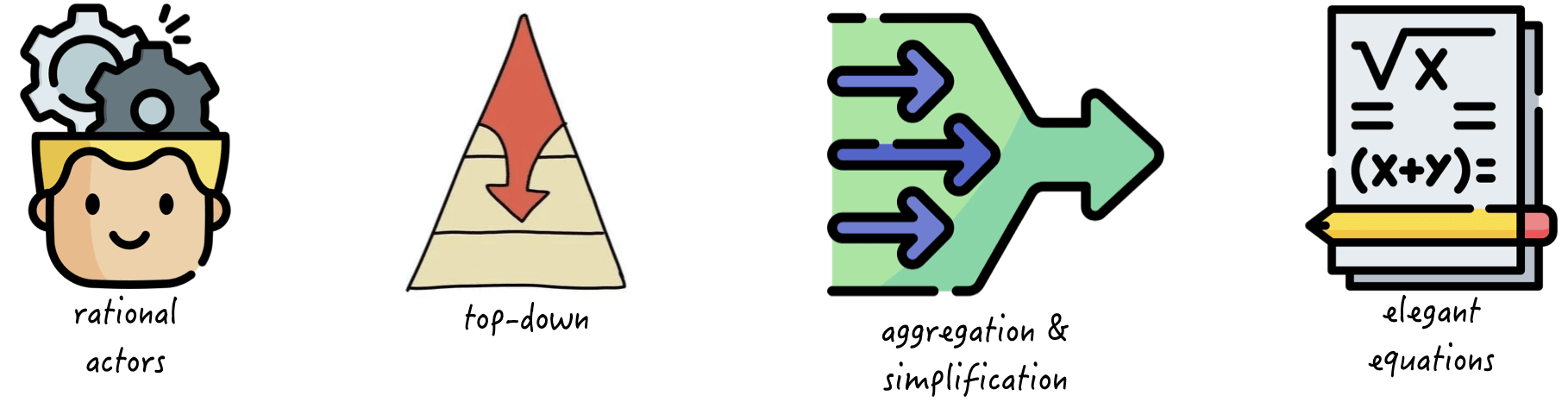
Traditional modeling, particularly in economics, is typically based on the assumption of rational actors making rational choices based on a cost-benefit analysis. This approach, known as rational choice theory, assumes that individuals will act in their own self-interest and maximize their utility based on a set of preferences and constraints. The resulting models are often based on elegant equations and mathematical frameworks and rely heavily on aggregation and simplification to make complex systems more manageable. This approach assumes a top-down view of the world, with individual behavior aggregated into macro-level patterns and trends.
However, this particular modeling style is ill-suited for dealing with complexity and uncertainty. The assumptions of rationality and self-interest are often oversimplified and do not accurately capture the full range of motivations and decision-making processes of individuals and groups. Additionally, the reliance on aggregation and simplification can obscure important details and interactions within the system, leading to inaccurate or incomplete models. This is particularly problematic when dealing with complex systems, where the interactions between different components and actors can be highly non-linear and unpredictable.
Furthermore, traditional modeling approaches often ignore the role of uncertainty and the potential for unexpected events or disruptions to occur. This is particularly problematic in complex systems, where small changes or perturbations can have significant and unexpected effects on the behavior of the system. The top-down view of traditional modeling approaches may also fail to capture the emergent behaviors and feedback loops that can arise from the interactions of multiple actors and components within the system.
Systems Modeling
So, while traditional modeling approaches based on rational choice theory and top-down aggregation have their strengths, they are ill-suited for dealing with complexity and uncertainty. To effectively model complex systems, new approaches are needed that embrace complexity and uncertainty and incorporate more nuanced and realistic assumptions about individual behavior and decision-making. The umbrella term of systems modeling offers a plethora of alternative modeling sub-paradigms. This includes agent-based modeling, discrete event simulation, and system dynamics modeling[1]. I consider agent-based modeling to be an especially potent paradigm that I would like to elaborate on.
Agent-Based Modeling
Agent-based modeling is an approach to modeling complex systems that focuses on the interactions and behaviors of individual agents within the system. In an agent-based model, each agent is represented as an individual entity with its own set of characteristics, behaviors, and decision-making processes. These agents interact with each other and with their environment, leading to emergent patterns and behaviors at the macro level.
The underlying assumption of agent-based modeling is that complex systems can be understood and predicted by modeling the interactions and behaviors of individual agents. This approach allows for more realistic and detailed modeling of individual behavior and interactions within the system and can capture the non-linear and unpredictable behavior that often characterizes complex systems.
Agent-based modeling typically involves the following steps: defining the agents, specifying their behaviors and decision-making processes, defining the environment, and simulating the behavior of the system over time. The behavior of each agent is based on a set of rules or algorithms that govern their decision-making processes, and the interactions between agents are modeled using communication channels or networks.
Example: Epidemic Disease Modeling
A relevant example is epidemic disease model as for example shown here[2]. Agent-based modeling allows for the modeling of individual behavior and interactions within a population. In an agent-based model of an epidemic, each agent represents an individual within the population and is assigned a set of characteristics, such as age, health status, and social network. The behavior and decision-making processes of each agent are then modeled based on a set of rules or algorithms that capture their interactions with other agents and with their environment. Using an agent-based model, researchers can simulate the spread of an epidemic through a population, and evaluate the potential effectiveness of different intervention strategies, such as vaccination, quarantine, or social distancing measures. The model can also be used to explore the impact of different variables on the spread of the disease, such as the rate of transmission, the incubation period, or the effectiveness of interventions. Agent-based modeling can provide several advantages over traditional epidemiological models, which often rely on simplified assumptions about population behavior and interaction. By modeling the behavior of individual agents, agent-based models can capture the heterogeneity and complexity of real-world populations, and account for the effects of social networks, geographic location, and other factors that can influence the spread of the disease.
Deep Uncertainty
There have been recent posts and other EA engagement with complexity science and systems modeling[3]. So, why add another? Using systems modeling is only one step of the research methods that I'm recommending EA researchers to use. The other step consists of conducting decision-making under deep uncertainty (DMDU). First, we need to address the question of what deep uncertainties are. We talk about deep uncertainties when parties to a decision do not know, or cannot agree on[4]
- the system model that relates action to consequences,
- the probability distributions to place over the inputs to these models, or
- which consequences to consider and their relative importance.
The first point (system model mapping) relates often to structural uncertainty in which we do not know how a natural system maps input and outputs. We are not certain about (some of) the underlying structures or functions within the formal model. The third point (consequence and relative importance) refers to the standard approach of oversimplification and aggregation and putting some a priori weights on several objectives. We will elaborate on this point further down the text. The second point (probability distributions) relates to that we do not know how likely particular values for particular input variables are. This is especially the case when we are looking at very rare events for which a frequentist probability is usually tricky. To elaborate on this, consider the table below. In this context, the literature distinguishes 5 levels of uncertainty[5].
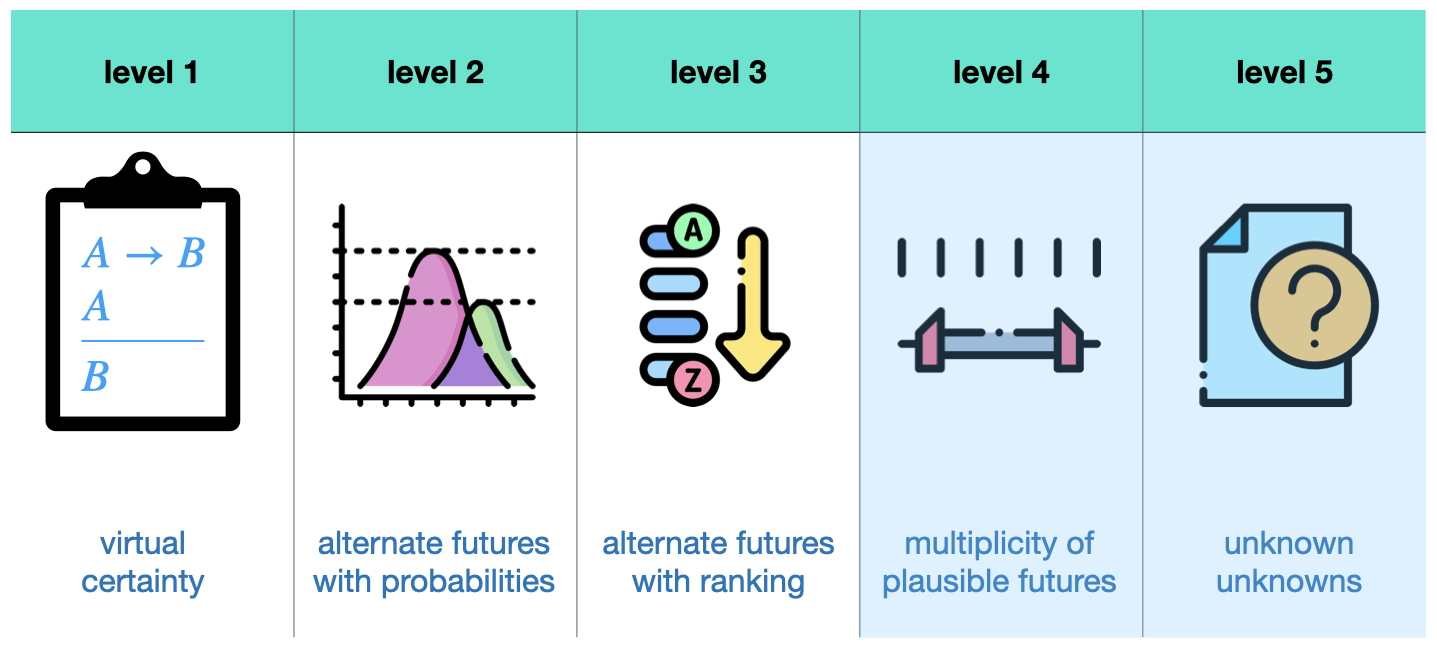
On the first level, you are looking at virtual certainty. It's (basically) a deterministic system. Level 2 uncertainty is the kind of uncertainty that most people refer to when they say uncertainty. It's the assumption that you know the probability distribution over alternate futures and is on a ratio scale [6]. Level 3 uncertainty is already rarer in its usage. It refers to alternate futures that you can only rank by their probabilities and is on an ordinal scale. In this case, we do not know the exact probabilities of future events but only which ones are more likely than others without indicating how much more likely.
Deep uncertainties refer to levels 4 and 5 uncertainties. Level 4 uncertainties refer to a situation in which you know about what outcomes are possible but you do not know anything about their probability distributions, not even the ranking. It's just a set of plausible futures. This is an extraordinarily important consideration! If true, this breaks expected-utility thinking.
Expected-Utility Thinking is in Trouble
In the absence of probability distributions, expected-utility thinking becomes useless, as it relies on accurate assessments of probabilities to determine the expected value of different options. How do you calculate expected utility if you do not know what to expect? Spoiler alert: You don't! Some would make the argument that we often do not know the probability distributions over many external factors that affect our systems. Sure, we know how likely a dice role is to yield a 5. But do we really know how likely it is that AGI will be devised, tested, and publicly announced by 2039? As Bayesians, we might tend to think that we can. But how useful are such kinds of probability distributions? A more modest position would consist in acknowledging that we do not know these probability distributions. We might argue that we know plausible date ranges. But this doesn't sit well with expected-utility thinking. Hence, deep uncertainties pose quite a challenge which we will address a bit later.
(Level 5 uncertainty refers to unknown unknowns that the suggested framework of DMDU can partially address with adaptive methods[7].)
Real-World Political Decision-Making
Real-world political decision-making is a complex and multi-faceted process that involves multiple actors at different scales and levels of governance. This system is characterized by deep uncertainties and multiple competing interests and values, making it difficult to arrive at effective and sustainable policy decisions.
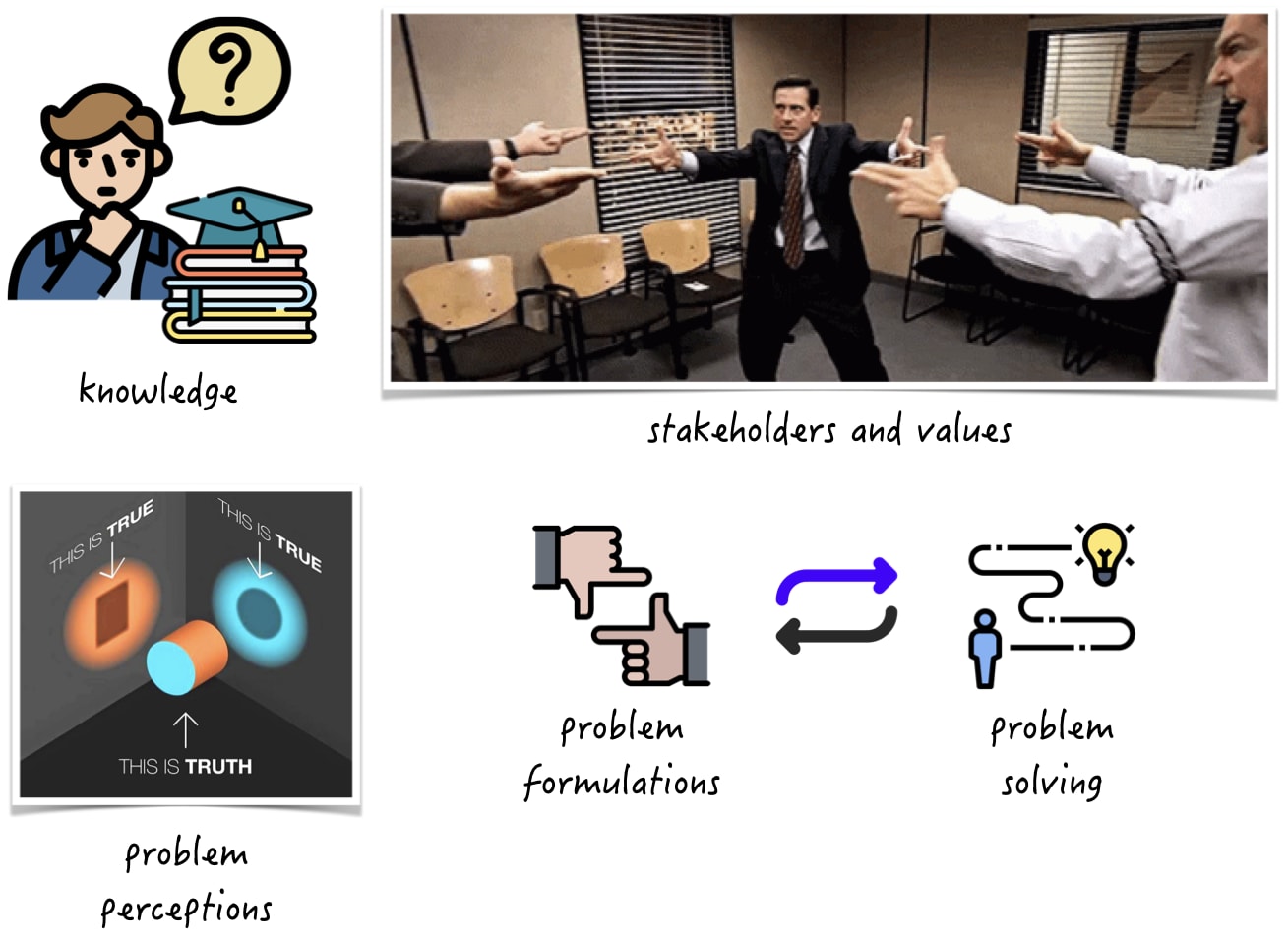
One key challenge of political decision-making is the inherent uncertainty of our knowledge. In many cases, we may not have complete or accurate information about a problem or its potential solutions, making it difficult to arrive at a consensus or make informed decisions. Additionally, different stakeholders may have different interpretations of the available information, leading to disagreements and conflicts over how to address a problem. Another challenge is the presence of multiple stakeholders with partially opposing values and interests. These actors may have different perspectives on a problem or different priorities for its solution, leading to disagreements and conflicts over policy options. Additionally, different actors may have different levels of power or influence within the decision-making system, which can affect the outcomes of the decision-making process. Yet another challenge is the existence of multiple ways of perceiving a problem or defining its scope. The framing or problem formulation can significantly affect the outcome of the decision-making process, as it can shape the way that stakeholders perceive and approach the problem. This can lead to different policy options or solutions being favored based on how the problem is framed.
Given all these challenges, what methods are we usually using to address real-world political decision-making? The short answer: We use inappropriate methods. Let's have a look at the diagram below.
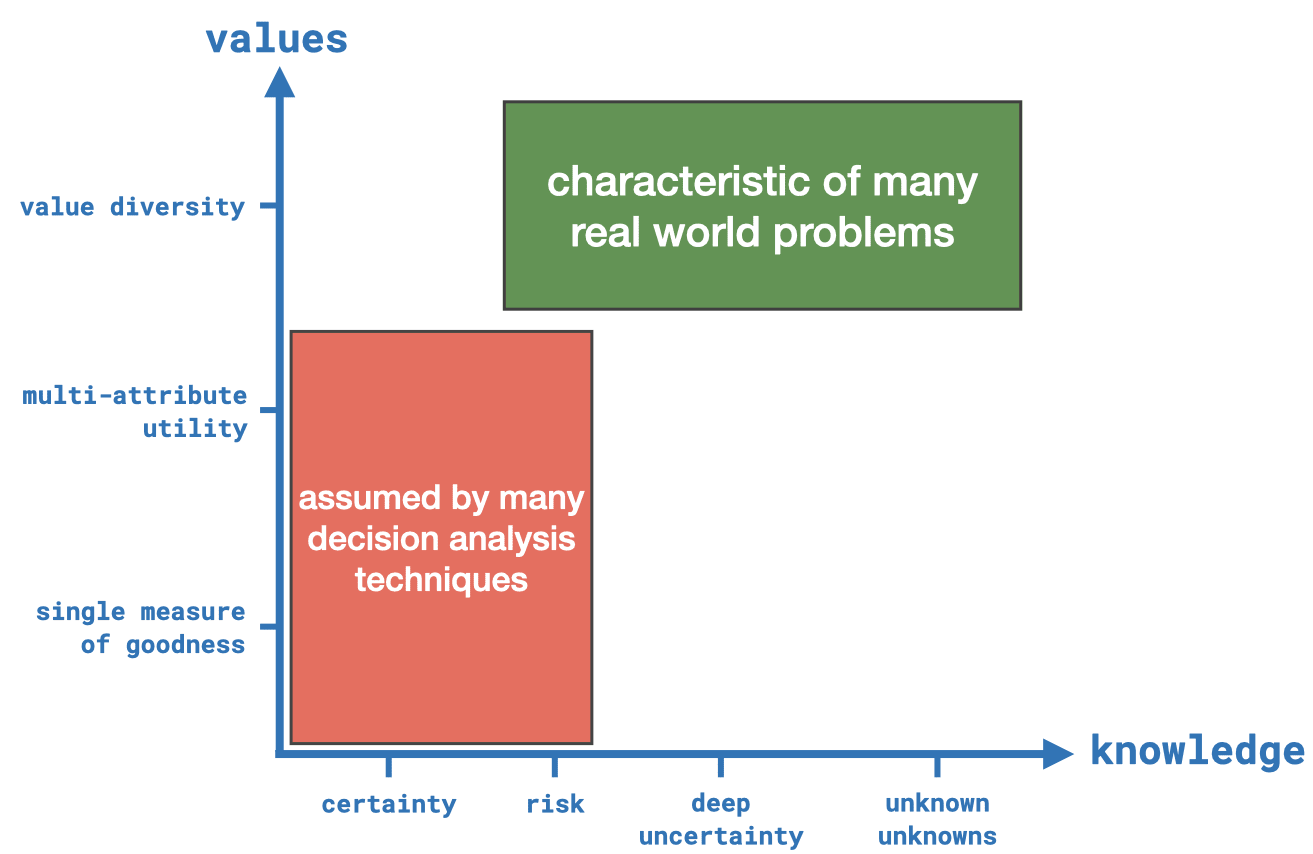
We have a space spanned by two dimensions: knowledge and values. We are looking at different levels of knowledge. The further we move to the right, the more uncertain things are getting. The vertical axis indicates what type of values we care about. The lowest one – a single measure of goodness – represents a single value, e.g., discounted aggregate welfare based on consumption as is typical in economics. The next level is a so-called multi-attribute utility which translates a set of relevant variables into a single utility value. Let's say, you care about the values welfare, equality, safety, and freedom. And let's assume you can somehow operationalize them in a model. In the framework of multi-attribute utility, you create a function that takes these as inputs and it outputs a utility value (or ranking over a bunch of futures). This is also a common way of aggregation and is considered by many as a good way how to handle multiple values. The last axis label is value diversity which does not aggregate your variables. You simply look at and optimize for various, potentially orthogonal values at the same time.
The standard decision analysis techniques assume that real-world political decision-making falls into the red area. We are certain about how systems work or we at least know the probability distributions over the inputs. And at the same time, a single measure or multi-attribute utility are appropriate ways to address the challenges of the real world. However, given our elaborations from above, real-world problems are more complex, exhibit deep uncertainties, and have many stakeholders with partially opposing values that are not easily aggregated. The obvious next question is: What methods can we use to address such problems? The answer is Decision-Making under Deep Uncertainty (DMDU).
Decision-Making under Deep Uncertainty
The DMDU process involves repeatedly considering different potential strategies, understanding their weaknesses, and evaluating the trade-offs between them to ultimately make informed decisions. It is commonly used by researchers to assess different options, but it is also utilized as a tool for decision support, focusing on assisting decision-makers in identifying and creating new options that are more robust. These options often involve adaptive strategies that can change over time in response to new information. DMDU can also be used to manage group decision-making in situations where parties have conflicting assumptions and values.
XLRM Framework
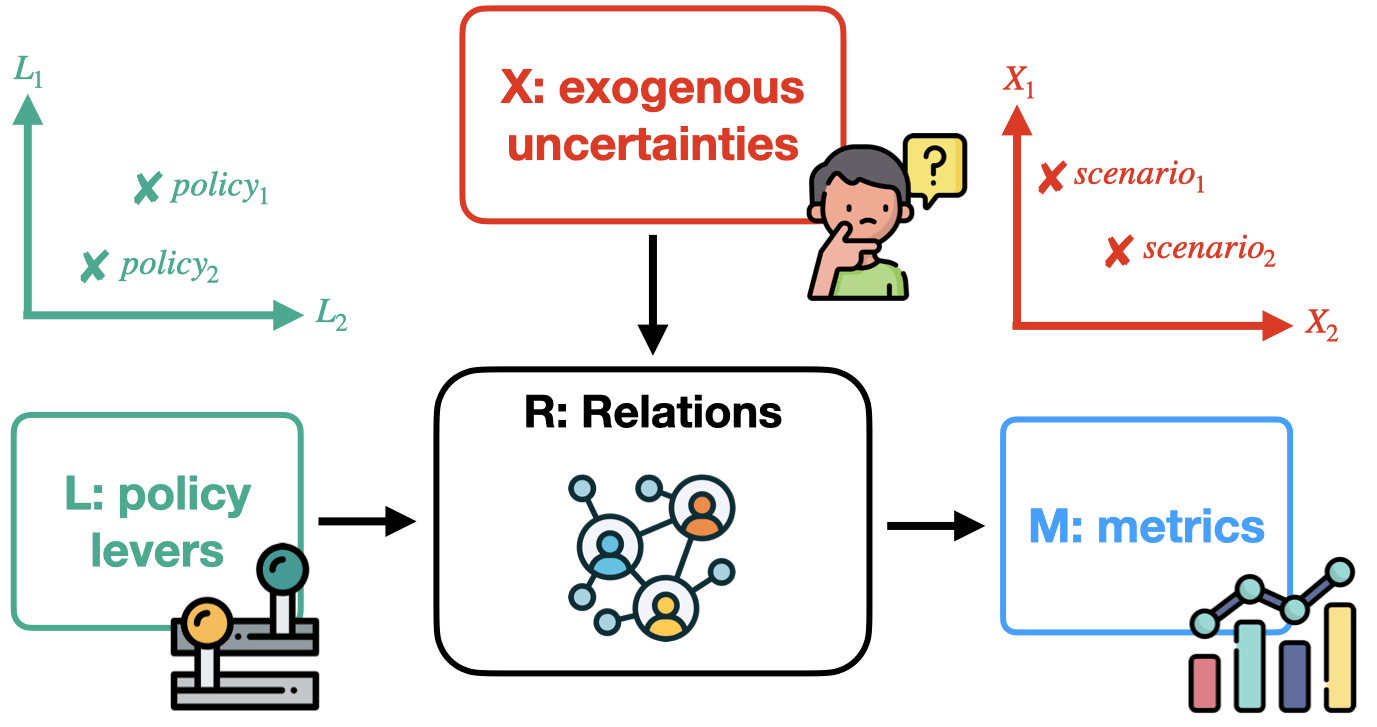
In order to explain better how DMDU works, let us look at a strongly abstracted standard model. Model information can be structured within the XLRM framework which was developed by RAND researchers[8]:
- X: Exogenous Uncertainties. These are variables that a decision-maker has no control over but will, however, still affect the system and therefore the performance of policies. All uncertainty variables span the uncertainty space. A point in that space is called a scenario.
- L: Policy Levers. These are variables that a decision-maker has control over and with which they can affect the system. All lever variables span the policy space. A point in that space is called a policy.
- R: Relations: This component refers to the inner workings of the system, describing a mapping between X and L on the one hand, and the metrics (M) on other hand.
- M: Performance Metrics: These are variables that a system outputs and that a decision-maker cares about.
The diagram below shows how levers and uncertainties are inputs to the model which is defined by its relations. This is model-paradigm-agnostic representation. The relations can be expressed by traditional modeling ways via simple mathematical equations, or by the rules than govern a particular agent-based system. The outputs of the model are our performance metrics.
Let's talk definitions. Within decision-making, a policy is a point in a lever space. If you have 2 orthogonal actions lever you can take, then a value combination of these two levers makes a policy. Let's say, for example, you can decide the savings rate for your household. It could range from [0.0, 1.0]. At the same time, you might want to decide how much time you want to spend on reading per week with a range of [0, 10] hours. These two actions span your policy space. Any combination is a possible policy.
Exogenous uncertainties work in a similar way. Every variable in your system that is uncertain spans together an uncertainty space. For example, you don't know how much money you will have available (maybe you are gambling or day trading). But you think that the range is between €[1000,4000]. And you don't know for how long your friend will stay over on the weekend, maybe something in the range of [Thursday, Monday]. Any given combination determines a scenario.
Your metrics can be various independent objectives that you have, e.g., number of pages read, quality of spent time with your friend, satisfaction with your savings, etc.
The relations would determine how to map the inputs with the outputs.
Predictive Modeling
As I see it, there are two different policy frameworks in this context.

In a predict-and-act policy framework, predictive models are used to anticipate the potential outcomes of different policy options or interventions, allowing policymakers to make more informed and effective decisions. Predictive modeling typically involves the following steps: defining the system and its components, specifying the relationships and interactions between the components, and simulating the behavior of the system over time. The resulting model can be used to explore different scenarios and evaluate the potential outcomes of different policy options or interventions. What is usually done by the modeler is a tweaking of single parameters and testing a handful of scenarios. This kind of work is quite manual, cumbersome, and often of limited use. Especially, as they are often caught by surprise.

What they often do is simply ignore uncertainties. Instead of using a full range (see the above example), they just collapse it into a single number. This is of course very problematic. When dealing with the real world, that makes little sense as some assumptions might likely be wrong. And in this case, your resulting policy recommendations become obsolete. Another way how predictive modelers handle deep uncertainties is summarized in the next meme.

Some predictive modelers vary their uncertain variables slightly, run their simulations a few times, and average the results. I guess, there is no need to emphasize how problematic this approach can be.
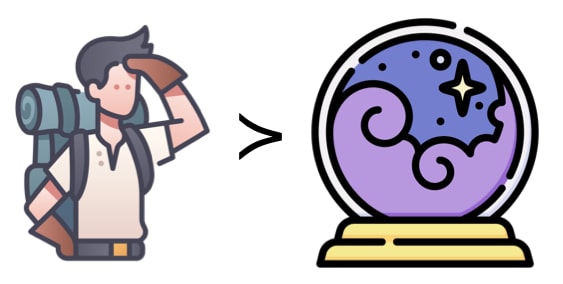
Generally, modelers do not have a magic crystal ball to look into the future. Ignoring uncertainties is not a sustainable solution. If you still want to use systems modeling, you might want to look for an alternative to predictive modeling.
Explorative Modeling
So, what's the alternative? Exploratory modeling is the use of computational experimentation to explore the implications of varying assumptions about uncertain, contested, or unknown model parameters and mechanisms. Here, we are talking about an explore-and-adapt policy framework. What we can do a bit more concretely is the following: Take your model and embed it in an optimization setup. Instead of manually changing some input parameters (policy levers and uncertainties) to see how they affect your metrics, you tell your optimizer to optimize your metrics and find the corresponding ideal policy levers. It is important to note that you do not want to maximize some kind of expected future performance. You want to minimize plausible future regret.

This approach makes it easy to avoid hand-picking values for your variables as you can explore the entire space. The results will be more useful and robust. As reasonable prediction is virtually impossible, exploration is preferred over prediction.
Multiple Objectives
Why would we need multiple objectives? We have touched upon this issue in a previous section. However, let us give it a bit more attention.
Arrow's Paradox, also known as Arrow's Impossibility Theorem, is a concept in social choice theory proposed by economist Kenneth Arrow in 1950. The theorem states that it is impossible to create a voting system that satisfies a set of fairness criteria when there are three or more options to choose from. These fairness criteria include unrestricted domain, non-dictatorship, Pareto efficiency, and independence of irrelevant alternatives. In simple terms, Arrow's Paradox suggests that no perfect voting system exists that can convert individual preferences into a collective, ranked preference list without violating at least one of these criteria. Disaggregation of multiple objectives in decision-making can help address Arrow's Paradox by breaking down complex decisions into smaller, more manageable components. By doing so, decision-makers can focus on one criterion at a time, allowing for more transparent and fair evaluations. This process enables the comparison of individual objectives using specific metrics, reducing the chance of preference inconsistencies that may arise in aggregated decisions.
Combining incommensurate variables in decision-making is akin to comparing apples and oranges, as these variables represent different dimensions and cannot be directly compared. Incommensurate variables are quantities that cannot be expressed in the same unit or do not share a common scale. When attempting to combine such variables, decision-makers may face difficulties in balancing the trade-offs between them, leading to potentially biased or suboptimal outcomes.

Take for example, economic consumption and climate damages in integrated assessment models. Although, they share the same unit (USD$ usually), it can be troublesome to conflate them into a single objective. Climate change is a complex, nonlinear process that involves multiple feedback loops and interactions. There is significant uncertainty associated with the magnitude and timing of future climate impacts, which makes it difficult to accurately quantify the damages caused by climate change. Beyond that, the impacts of climate change are not evenly distributed across the population or the world. Some regions and populations are more vulnerable to the effects of climate change than others. Therefore, aggregating economic consumption and climate damages into a single variable may obscure important distributional impacts and equity considerations. Often, it might be better to consider separate objectives to avoid such pitfalls.
Generally, premature aggregation can be bad in general because it can oversimplify complex phenomena and obscure important details and nuances. Premature aggregation can result in the loss of important information about the underlying factors that contribute to the data. This loss of information can lead to biased or incomplete assessments of the data and mask important trends or patterns. Aggregation can oversimplify complex phenomena by collapsing multiple dimensions into a single measure or index. This oversimplification can result in inaccurate or misleading conclusions and mask important trade-offs and uncertainties. And eventually, aggregation can also hide underlying assumptions and modeling choices that may influence the results of the analysis. These hidden assumptions can make it difficult to compare the results of different models or assess the robustness of the results.

At this point, you are probably asking yourself, how do we optimize for multiple objectives at the same time? The answer is: We use multi-objective evolutionary algorithms. That is at least the standard practice in the field of DMDU.
Usually, you have only one objective which looks something like this:
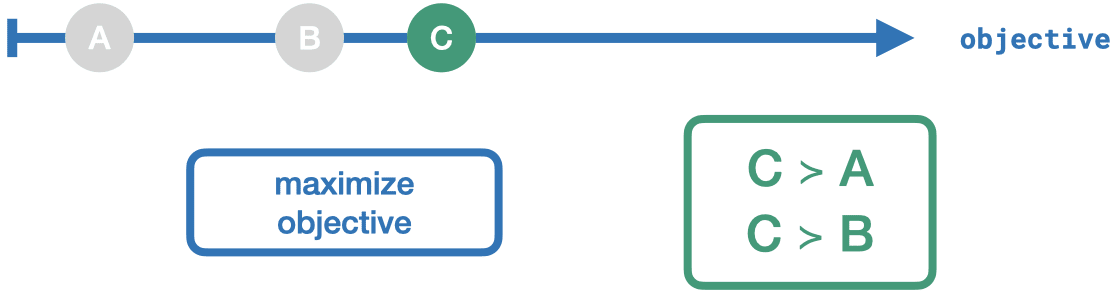
You have three outcomes for one objective. It's clear which outcome is dominating. But if we add another objective, things become more complicated – but still doable!
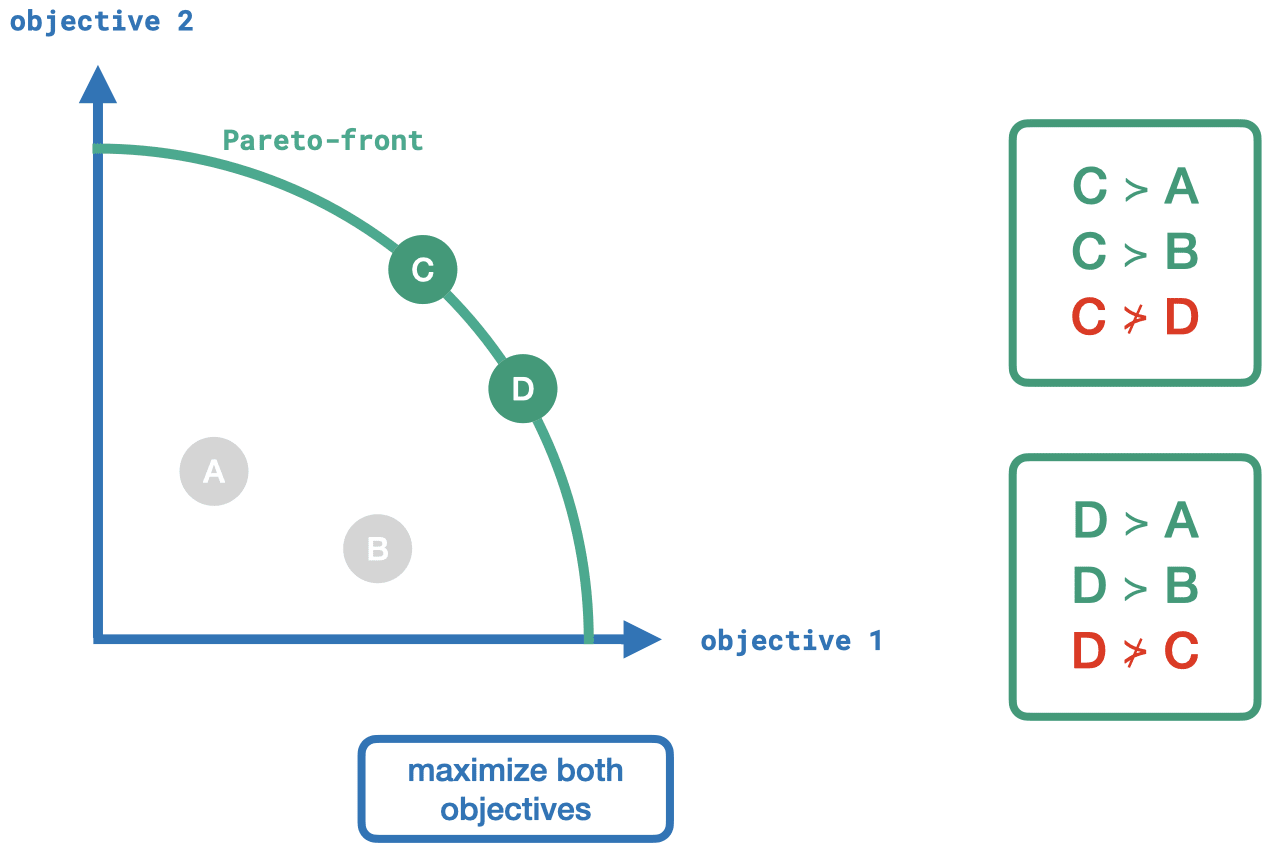
We can see that both, C and D, dominate A and B. But neither C nor D dominates each other. We consider outcomes C and D to be part of the so-called Pareto-front.
We can use these concepts in evolutionary algorithms to determine better and better policy solutions while optimizing multiple objectives simultaneously. Usually, we end up with a set of Pareto-optimal solutions that exhibit different trade-offs over the objectives.
Example Method: MORDM
Let's make it even more concrete by looking at a particular method. Within the DMDU framework, there is an approach that is called multi-objective robust decision-making (MORDM)[9]. An abstraction of the model is shown below.

First, we specify the parameters and ranges of your model. Then, we need to determine the scenarios that we want to run the optimizations on later. As we admit that we do not know the probability distributions over our uncertainties, we can sample particular scenarios from the uncertainty space. DMDU is intended to consider worst-case scenarios and find robust policy solutions. That is why we need to identify particularly vulnerable scenarios. That means that we are looking for a combination of uncertainty values that impact our metrics in a very bad way. For this purpose, we usually use some kind of AI algorithm. If we find a handful of such scenarios that are sufficiently vulnerable and diverse, we can to the next step of the MORDM process – policy discovery. Given a vulnerable scenario, and a set of objectives with their desired optimization direction, we use multi-objective evolutionary algorithms to find a set of Pareto-optimal policies. (We can do this in parallel for each vulnerable scenario.) In the next step, we sample a wide range of scenarios from the uncertainty space and re-evaluate how well our Pareto-optimal policies perform. They were optimal for the chosen reference scenarios. But that does not entail that they will be optimal or even okay in other random scenarios. However, usually, we can identify a few policies that still perform well enough in many different scenarios. If not, we feed back this information to zoom in on particular subspaces of the uncertainty space and re-iterate the process to find better and better solutions for vulnerable scenarios that perform also well in more favorable scenarios. In the end, we conduct a trade-off analysis.
Scenario Selection
Instead of fixing all uncertainties, or handcrafting a handful of scenarios, what we usually do is sampling thousands of scenarios. Consider for example an uncertainty space of only two uncertainty variables. Sampling from that space with uniform distributions per axis (or slightly more sophisticated sampling methods such as Latin hypercube sampling) will result in the figure below.

Every dot represents one scenario. What we usually want to do, is finding the vulnerable subspace, i.e. the space where we find the scenarios which lead to the most bad outcomes (e.g., defined by some constraints on our objectives). The red dots in the figure below represent such bad scenarios. The red box marks the vulnerable subspace. Note that there are also okay scenarios in that box but that is fine. We do not need to define a subspace that contains only scenarios with bad outcomes. A rough subspace where more scenarios bad outcomes are predominant is sufficient.
What we do next is selecting particular scenarios in that vulnerable subspace that represent the subspace in the best way. So, we are looking for scenarios that are vulnerable but also maximally diverse. In the figure below, you see these scenarios as black dots. (These have been randomly put in place for this example. There are formal methods to find these scenarios but we will not discuss them here.)

These three scenarios would represent our reference scenarios. We would use these for our policy discovery process with our evolutionary algorithms to find Pareto-optimal policy solutions. From there, we continue with reevaluation under deep uncertainty, scenario discovery, etc.
This should just represent a teaser for what it is like to use this kind of methodology.
Example Plots
The visual outputs can be quite diverse. But I would like to show 3 examples.
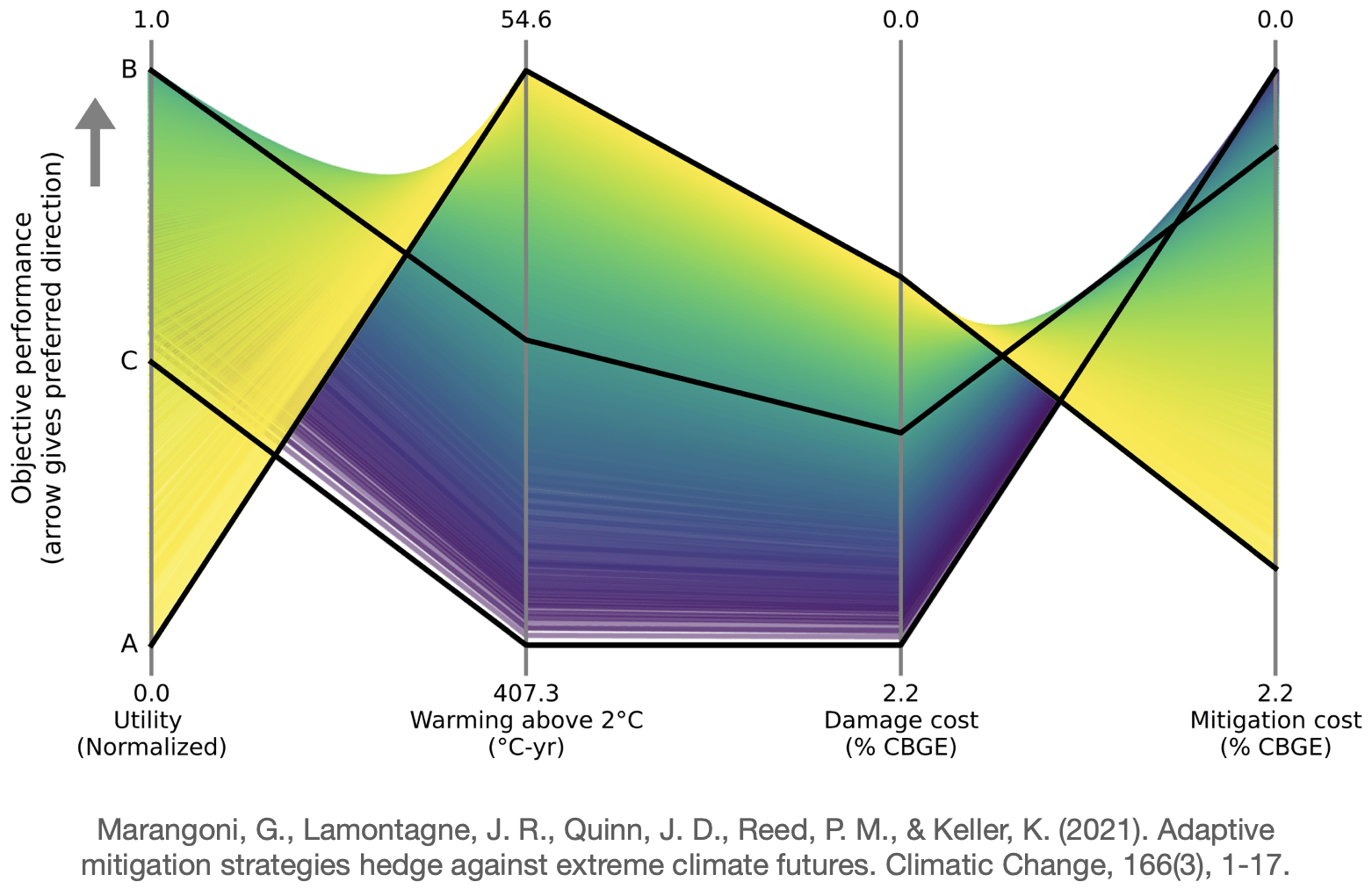
The first example is a so-called parallel-axes plot[11]. Each vertical axis represents an objective. Values at the top of the axis are considered more desirable. A line that runs through all axes is one particular outcome of a model run. For example, the black line A exhibits undesirably low utility, desirably low warming above 2 degrees Celsius, medium damage costs, and a not-so-desirable amount of mitigation costs. This shows a trade-off. Line B exhibits a different trade-off. If you look closely, you can see many more lines. And from this, you can conclude more general patterns and trade-offs. (All these outcomes are based on optimal policies in various scenarios.)
There are also other plots such as subway plots which depict tipping points in the future to indicate a change to a different policy[13]. Each colored lined represents one policy. Every ring is a transfer station to a different policy. As we can observe, it is not always possible to transfer to any other policy. And sometimes there are terminal points that indicate that we cannot transfer at all anymore.
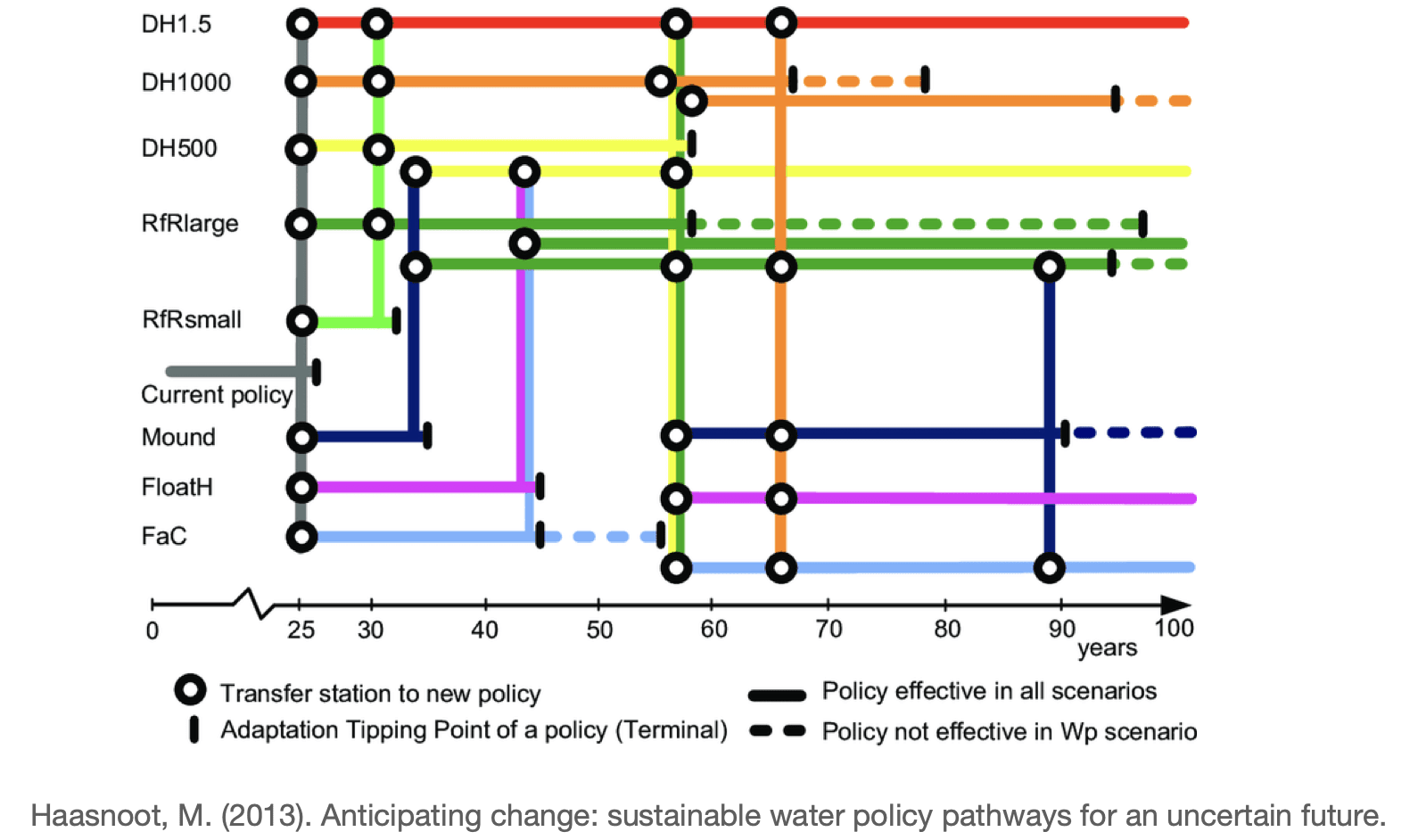
These plots are supposed to be teasers for how visual deliverables could look when using DMDU techniques.
Potential Drawbacks
The three main drawbacks of using DMDU are depicted in the memes below.

Con: Encoding a Complex World into Simple Models
The first drawback is one that refers more to encoding complex models in general. Complex models often involve a large number of variables and parameters, making it difficult to represent the full complexity of the system in a formal model. This can lead to oversimplification or abstraction of important details, which may affect the accuracy or validity of the model. Even when we use DMDU and embrace uncertainties instead of ignoring them, we still have to make a lot of assumptions and decisions throughout the modeling process. Furthermore, complex models involve non-linear or dynamic interactions between different variables, which can be difficult to capture in a formal model. This can lead to the development of models that are overly simplified or do not accurately reflect the true behavior of the system. Verification and validation can be very hard. Moreover, encoding complex models can be time-consuming and resource-intensive, requiring significant expertise and computational resources to develop and test the model. This can limit the applicability of the model or make it difficult to develop models that are accessible to a wide range of stakeholders.
Con: Stakeholder Cognitive Overload
Predictive modelers can offer point predictions to stakeholders. That is easy to understand and might feel actionable. The DMDU outputs are of explorative nature and involve a lot of scenarios, caveats, trade-offs, and insights. Communicating this can be a challenge. If not done with care, all the analysis might be futile, if the stakeholder is unable or unwilling to be walked through the complexities of the model and the trade-offs of available policy options.
Con: Compute
Running for example an agent-based model can require a lot of computing. Some models run in a few minutes, some might need a few hours on a laptop. Running optimizations with such models with many many iterations can take weeks, months, or years. This depends of course on the complexity of your model, how many agents you have, how many interactions they have, how many objectives, uncertainties, and policy levers you use, and what kind of datatypes you use (are you uncertainties binary, nominal, a finite set of values, or range between two floats?). Given enough resources, we should be able to overcome this particular problem.
Conclusion
I hope that this post was able to show you why I think this approach could be so valuable. The world is complex. Policy-making is hard. Modeling can help if we use systems modeling in particular. Decision-making under deep uncertainty is an excellent tool to leverage these models even better. I think that the following meme is the most important one in this post and it is what I like the reader to take away from.

Decision-making under deep uncertainty seems to me like a natural fit with EA's efforts to address global catastrophic risks, existential risks, and suffering risks. We are looking purposefully at very undesirable future scenarios and attempting to find policy solutions that would be robust, rendering worst-case scenarios less bad. In other words, we can use these techniques to strengthen societal resilience. I see the most relevant application areas of this methodology in:
- Biorisk
- Economics
- Improving Institutional Decision-Making
- Climate Change
- Nuclear War
- AI Governance
- Longtermism
I would be happy to talk to anyone that has remaining questions or is interested in using this methodology for EA-motivated projects. I'm particularly interested in applying model-based policy analysis under deep uncertainty on AI governance.
Additional Resources
On Modeling
On Deep Uncertainty
- Book: Decision Making under Deep Uncertainty
- Book: Shaping the Next One Hundred Years: New Methods for Quantitative, Long-Term Policy Analysis
- Book: Evolutionary Algorithms for Solving Multi-Objective Problems
- Website: DMDU Society
- DMDU Memes
- ^
An excellent resource for exploring various model paradigms is Scott E. Page's book The Model Thinker: What You Need to Know to Make Data Work for You (2018).
- ^
You can use this link to play around with the parameters and observe the emerging macro behaviors.
- ^
- ^
Walker, W. E., Lempert, R. J., & Kwakkel, J. H. (2012). Deep uncertainty. Delft University of Technology, 1(2).
- ^
Walker, W. E., Lempert, R. J., & Kwakkel, J. H. (2012). Deep uncertainty. Delft University of Technology, 1(2).
- ^
E.g., a fair dice has a uniform distribution of 1/6 over all 6 outcomes. Mind that there does not have to be a uniform distribution to be considered level 2 uncertainty.
- ^
However, I will not focus on adaptive methods in this post. For more information, see for example:
Maier, H. R., Guillaume, J. H., van Delden, H., Riddell, G. A., Haasnoot, M., & Kwakkel, J. H. (2016). An uncertain future, deep uncertainty, scenarios, robustness and adaptation: How do they fit together?. Environmental modelling & software, 81, 154-164.
Walker, W. E., Haasnoot, M., & Kwakkel, J. H. (2013). Adapt or perish: A review of planning approaches for adaptation under deep uncertainty. Sustainability, 5(3), 955-979.
Hamarat, C., Kwakkel, J. H., & Pruyt, E. (2013). Adaptive robust design under deep uncertainty. Technological Forecasting and Social Change, 80(3), 408-418.
- ^
Lempert, R. J. (2003). Shaping the next one hundred years: new methods for quantitative, long-term policy analysis.
- ^
Kasprzyk, J. R., Nataraj, S., Reed, P. M., & Lempert, R. J. (2013). Many objective robust decision making for complex environmental systems undergoing change. Environmental Modelling & Software, 42, 55-71.
- ^
Kasprzyk, J. R., Nataraj, S., Reed, P. M., & Lempert, R. J. (2013). Many objective robust decision making for complex environmental systems undergoing change. Environmental Modelling & Software, 42, 55-71.
- ^
Marangoni, G., Lamontagne, J. R., Quinn, J. D., Reed, P. M., & Keller, K. (2021). Adaptive mitigation strategies hedge against extreme climate futures. Climatic Change, 166(3-4), 37.
- ^
This plot can be found in a notebook of Jan Kwakkel for a course on Model-Based Decision-Making.
- ^
Haasnoot, M. (2013). Anticipating change: sustainable water policy pathways for an uncertain future.

Thanks for sharing this! I'm very much in favour of looking for more robustly positive interventions and reducing sensitivity to arbitrary beliefs or modeling decisions.
I think it’s worth pointing out that minimizing regret is maximally ambiguity averse, which seems controversial philosophically, and may mean giving up enormous upside potential or ignoring far more likely bad cases. In a sense, it’s fanatically worst case-focused. I suppose you could cut out the most unlikely worst cases (hence minimizing "plausible future regret"), but doing so is also arbitrary, and I don’t know how you would want to assess "plausibility".
I might instead make the weaker claim that we should rule out robustly dominated portfolios of interventions, but this might not rule out anything (even research and capacity building could end up being misused): https://forum.effectivealtruism.org/posts/Mig4y9Duu6pzuw3H4/hedging-against-deep-and-moral-uncertainty
And thank you for sharing your thoughts on this matter!
Indeed, focusing on hyper-unrealistic worst cases would be counter-productive in my view. Your arbitrary-objection is a justified one! However, there is some literature in this field engaging with the question of how to select or discover relevant scenarios. I think, there are some methods and judgment calls to handle this situation more gracefully than just waving one's hand.
And I agree with your statement and linked post that the weaker claim is easier to accept. In practice, I would probably still go beyond and use decision-making under deep uncertainty to inform the policy-making process. This seems to be a still better approach than the default.
What you can also do is still handcrafting scenarios as it is done for climate change mitigation. You have various shared socioeconomic pathways (SSPs) created by a lot of experts. You could attempt to find policy solutions that would perform sufficiently well for SSP4 or SSP5. But in the end, it might be just very useful to involve the stakeholders and let them co-decide these aspects.
As someone who works on probabilistic programming (w applications to simulation based modeling), I wanted to say that I thought this was very good! I think more people attracted to expected utility maximization should read this to expand their view of what's possible and practical in light of our value disagreements, and our deep ignorance about the world.
Thank you for sharing your thoughts! I think, for me, it was the case for a long time that I just didn't know about alternative approaches. E.g., what else would you do if not maximizing expected utility? And if you want to do optimization (of utility), what else is there but aggregating all your values into a single utility? Well, using multi-objective optimization (Pareto-optimality) and seeking robust solutions are alternatives. So, that changed my outlook at least.
Thank you for this post, overall I think it is interesting and relevant at least for my interests. There was one thing I wanted clarification on, however:
I’m often confused by these kinds of claims, as I don’t fully understand the assertion and/or problem here: if you genuinely cannot do better than assigning 1/n probability to each of n outcomes, then that is a legitimate distribution that you could use for expected-utility calculations. The reality is that oftentimes we do know at least slightly better than pure ignorance, but regardless, I’m just struggling to see why even pure ignorance is such a problem for expected utility calculations which acknowledge this state of affairs?
I think assigning 1/n typically depends on evidential symmetry (like simple cluelessness) or at least that the reasons all balance out precisely, so rules out complex cluelessness. Instead, we might have evidence for and against each possibility, but be unable to weigh it all without making very arbitrary assumptions, so we wouldn't be wiling to commit to the belief that A is more likely than B or vice versa or that they're equally likely. There's an illustrative example here.
Similarly, Brian Tomasik claimed, after looking into many different effects and considerations:
But if he had built formal models with precise probabilities, it would almost certainly have come out with climate change bad in expectation or climate change good in expectation, rather than net neutral in expectation, and the expected impact could be (but wouldn’t necessarily be) very very large. But someone else with slightly different (but pretty arbitrary) precise probabilities could get the opposite sign and still huge expected impact. It would seem bad to bet a lot on one side if the sign and magnitude of the expected value is sensitive to arbitrarily chosen numbers.
Even if multiple people come up with different numbers and we want to weigh them, there's still a question of how exactly to weigh them given possibly different levels of relevant expertise and bias between them, so 1/n is probably wrong, but all other approaches to come up with single precise numbers are going to involve arbitrary parameters/weights.
I wonder if the problem here is a failure to disentangle “what is our best estimate currently” and “what do we expect is the value of doing further analysis, given how fragile our current estimates are.”
If my research agent Alice said “I think there’s a 50% chance that doing X leads to +2,000,000,000 utils and a 50% chance that doing X leads to -1,000,000,000 utils (and the same probabilities that not doing X leads to the opposite outcomes), but these probability estimates are currently just pure 1/n uncertainty; such estimates could easily shift over time pending further analysis” I would probably say “wow I don’t like the uncertainty here, can we maybe do further analysis to make sure we’re right before choosing to do X?”
In other words, the concern seems to be that you don’t want to misrepresent the potential for new information to change your estimates.
However, suppose Alice actually says “… and no matter how much more research effort we apply (within real-world constraints) we are confident that our probability estimates will not meaningfully change.” At that point, there is no chance at improving, so you are stuck with pure, 1/n ignorance.
Perhaps I’m just unclear what it would even mean to be in a situation where you “can’t” put a probability estimate on things that does as good as or better than pure 1/n ignorance. I can understand the claim that in some scenarios you perhaps “shouldn’t” because it risks miscommunicating about the potential value of trying to improve your probability estimates, but that doesn’t seem like an insurmountable problem (I.e., we could develop better terms and communication norms for this)?
I'm not sure exactly what you mean by this, and I expect this will make it more complicated to think about than just giving utility differences with the counterfactual.
The idea of sensitivity to new information has been called credal resilience/credal fragility, but the problem I'm concerned with is having justified credences. I would often find it deeply unsatisfying (i.e. it seems unjustifiable) to represent my beliefs with a single probability distribution; I'd feel like I'm pulling numbers out of my ass, and I don't think we should base important decisions on such numbers. So, I'd often rather give ranges for my probabilities. You literally can give single distributions/precise probabilities, but it seems unjustifiable, overconfident and silly.
If you haven't already, I'd recommend reading the illustrative example here. I'd say it's not actually justifiable to assign precisely 50-50 in that case or in almost any realistic situation that actually matters, because:
For the same reasons, in almost any realistic situation that actually matters, Alice in your example could not justifiably get 50-50. And in general, you shouldn't get numbers with short exact decimal or fractional representations.
So, say in your example, it comes out 51.28... to 48.72..., but could have gone the other way under different reasonable parameter assignments; those are just the ones Alice happened to pick at that particular time. Maybe she also tells you it seems pretty arbitrary, and she could imagine having come up with the opposite conclusion and probabilities much further from 50-50 in each direction. And that she doesn't have a best guess, because, again, it seems too arbitrary.
How would you respond if there isn't enough time to investigate further? But you could instead support something that seems cost-effective without being so sensitive to pretty arbitrary parameter assignments, but not nearly as cost-effective as Alice's intervention or an intervention doing the opposite.
Also imagine Bob gets around 47-53, and agrees with Alice about the arbitrariness and reasonable ranges. Furthermore, you can't weigh Alice and Bob's distributions evenly, because Alice has slightly more experience as a researcher and/or a slightly better score in forecasting, so you should give her estimate more weight.
Great to see people digging into the crucial assumptions!
In my view, @MichaelStJules makes great counter points to @Harrison Durland's objection. I would like to add to further points.
I’m not sure I understand the concern with (1); I would first say that I think infinities are occasionally thrown around too lightly, and in this example it seems like it might be unjustified to say there are infinite possible values, especially since we are talking about units of people/population (which is composed of finite matter and discrete units). Moreover, the actual impact of a difference between 1.0000000000002% and 1.00000000000001% in most values seems unimportant for practical decision-making considerations—which, notably, are not made with infinite computation and data and action capabilities—even if it is theoretically possible to have such a difference. If something like that which seems so small is actually meaningful (e.g., it flips signs), however, then that might update you towards beliefs like “within analytical constraints the current analysis points to [balancing out |OR| one side being favored].” In other words, perhaps not pure uncertainty, since now you plausibly have some information that leans one way or another (with some caveats I won’t get into).
I think I would agree to some extent with (2). My main concern is mostly that I see people write things that (seemingly) make it sound like you just logically can’t do expected utility calculations when you face something like pure uncertainty; you just logically have to put a “?” in your models instead of “1/n,” which just breaks the whole model. Sometimes (like the examples I mentioned), the rest of the model is fine!
I contest that you can use “1/n”, it’s more just a matter of “should you do so given that you run the risk of misleading yourself or your audience towards X, Y, and Z failure modes (e.g., downplaying the value of doing further analysis, putting too many eggs in one basket/ignoring non-linear utility functions, creating bad epistemic cultures which disincentivize people from speaking out against overconfidence, …).”
In other words, I would prefer to see clearer disentangling of epistemic/logical claims from strategic/communication claims.
"While useful, even models that produced a perfect probability density function for precisely selected outcomes would not prove sufficient to answer such questions. Nor are they necessary."
I recommend reading DMDU since it goes into much more detail than I can do justice.
Yet, I believe you are focusing heavily on the concept of the distribution existing while the claim should be restated.
Deep uncertainty implies that the range of reasonable distributions allows so many reasonable decisions that attempting to "agree on assumptions then act" is a poor frame. Instead, you want to explore all reasonable distributions then "agree on decisions".
If you are in a state where reasonable people are producing meaningfully different decisions, ie different sign from your convention above, based on the distribution and weighting terms. Then it becomes more useful to focus on the timeline and tradeoffs rather than the current understanding of the distribution:
Explore the largest range of scenarios (in the 1/n case each time you add another plausible scenario it changes all scenario weights)
Understand the sequence of actions/information released
Identify actions that won't change with new info
Identify information that will meaningfully change your decision
Identify actions that should follow given the new information
Quantify tradeoffs forced with decisions
This results is building an adapting policy pathway rather than making a decision or even choosing a model framework.
Value is derived from expanding the suite of policies, scenarios and objectives or illustrating the tradeoffs between objectives and how to minimize those tradeoffs via sequencing.
This is in contrast to emphasizing the optimal distribution (or worse, point estimate) conditional on all available data. Since that distribution is still subject to change in time and evaluated under different weights by different stakeholders.
I just added this in hastily to address any objection that says something like “What if I’m risk averse and prefer a 100% chance of getting 0 utility instead of an x% chance of getting very negative utility.” It would probably have been better to just say something like “ignore risk aversion and non-linear utility.”
I think this boils down to my point about the fear of miscommunicating—the questions like “how should I communicate my findings,” “what do my findings say about doing further analysis,” and “what are my findings current best-guess estimates.” If you think it goes beyond that—that it is actually “intrinsically incorrect-as-written,” I could write up a longer reply elaborating on the following: I’d pose the question back at you and ask whether it’s really justified or optimal to include ambiguity-laden “ranges” assuming there will be no miscommunication risks (e.g., nobody assumes “he said 57.61% so he must be very confident he’s right and doing more analysis won’t be useful”)? If you say “there’s a 1%-99% chance that a given coin will land on heads” because the coin is weighted but you don’t know whether it’s for heads or tails, how is this functionally any different from saying “my best guess is that on one flip the coin has a 50% chance of landing on heads”? (Again, I could elaborate further if needed)
Sure, I agree. But that doesn’t change the decision in the example I gave, at least when you leave it at “upon further investigation it’s actually about 51-49.” In either case, the expected benefit-cost ratio is still roughly around 2:1. When facing analytical constraints and for this purely theoretical case, it seems optimal to do the 1/n estimate rather than “NaN” or “” or “???” which breaks your whole model and prevents you from calculating anything, so long as you’re setting aside all miscommunication risks (which was the main point of my comment: to try to disentangle miscommunication and related risks from the ability to use 1/n probabilities as a default optimal). To paraphrase what I said for a different comment, in the real world maybe it is better to just throw a wrench in the whole model and say “dear principal: no, stop, we need to disengage autopilot and think longer.” But I’m not at the real world yet, because I want to make sure I am clear on why I see so many people say things like you can’t give probability estimates for pure uncertainty (when in reality it seems nothing is certain anyway and thus you can’t give 100.0% “true” point or range estimates for anything).
Suppose you think you might come up with new hypotheses in the future which will cause you to reevaluate how the existing evidence supports your current hypotheses. In this case probabilistically modelling the phenomenon doesn’t necessarily get you the right “value of further investigation” (because you’re not modelling hypothesis X), but you might still be well advised to hold off acting and investigate further - collecting more data might even be what leads to you thinking of the new hypothesis, leading to a “non Bayesian update”. That said, I think you could separately estimate the probability of a revision of this type.
Similarly, you might discover a new outcome that’s important that you’d previously neglected to include in your models.
One more thing: because probability is difficult to work with, even if it is in principle compatible with adaptive plans, it might in practice tend to steer away from them.
I basically agree (although it might provide a decent amount of information to this end), but this does not reject the idea that you can make a probability estimate equally or more accurate than pure 1/n uncertainty.
Ultimately, if you want to focus on “what is the expected value of doing further analyses to improve my probability estimates,” I say go for it. You often shouldn’t default to accepting pure 1/n ignorance. But I still can’t imagine a situation that truly matches “Level 4 or Level 5 Uncertainty,” where there is nothing as good as or better than pure 1/n ignorance. If you truly know absolutely and purely nothing about a probability distribution—which almost never happens—then it seems 1/n estimates will be the default optimal distribution, because anything else would require being able to offer supposedly-nonexistent information to justify that conclusion.
Ultimately, a better framing (to me) would seem like “if you find yourself at 1/n ignorance, you should be careful not to accept that as a legitimate probability estimate unless you are really rock solid confident it won’t improve.” No?
I think this question - whether it's better to take 1/n probabilities (or maximum entropy distributions or whatever) or to adopt some "deep uncertainty" strategy - does not have an obvious answer
I actually think it probably (pending further objections) does have a somewhat straightforward answer with regards to the rather narrow, theoretical cases that I have in mind, which relate to the confusion I had which started this comment chain.
It’s hard to accurately convey the full degree of my caveats/specifications, but one simple example is something like “Suppose you are forced to choose whether to do X or nothing (Y). You are purely uncertain whether X will lead to outcome Great (Q), Good (P), or Bad (W), and there is guaranteed to be no way to get further information on this. However, you can safely assume that outcome Q is guaranteed to lead to +1,000 utils, P is guaranteed to lead to +500 utils, and W is guaranteed to lead to -500 utils. Doing nothing is guaranteed to lead to 0 utils. What should you do, assuming utils do not have non-linear effects?”
In this scenario, it seems very clear to me that a strategy of “do nothing” is inferior to doing X: even though you don’t know what the actual probabilities of Q, P, and W are, I don’t understand how the 1/n default will fail to work (across a sufficiently large number of 1/n cases). And when taking the 1/n estimate as a default, the expected utility is positive.
Of course, outside of barebones theoretical examples (I.e., in the real world) I don’t think there is a simple, straightforward algorithm for deciding when to pursue more information vs. act on limited information with significant uncertainty.
Good point! I think this is also a matter of risk aversion. How severe is it to get to a state of -500 utils? If you are very risk-averse, it might be better to do nothing. But I cannot make such a blanket statement.
I'd like to emphasize at this point that the DMDU approach is trying to avoid to
Instead, we use DMDU to consider the full range of plausible scenarios to explore and identify particularly vulnerable scenarios. We want to pay special attention to these scenarios and find optimal and robust solutions for them. Like this, we cover tail risks which is quite in line IMO with mitigation efforts of GCRs, x-risks, and s-risks.
I would disagree with this particular statement. I'm not saying the opposite either. I think, it's reasonable in a lot of cases to assume some probability distributions. However, there are lot of cases, where we just do not know at all. E.g., take the space of possible minds. What's our probability distribution of our first AGI over this space? I personally don't know. Even looking at binary events – What's our probability distribution for AI x-risk this century? 10%? I find this widely used number implausible.
But I agree that we can try gathering more information to get more clarity on that. What is often done in DMDU analysis is that we figure out that some uncertainty variables don't have much of an impact on our system anyway (so we fix the variables to some value) or that we constrain their value ranges to focus on more relevant subspaces. The DMDU framework does not necessitate or advocate for total ignorance. I think, there is room for an in-between.
@Vanessa Kosoy has a nice explanation of Level 4 uncertainties (a.k.a as Knightian uncertainty), in the context of her work on infra-Bayesianism. The following is from her AXRP podcast interview with @DanielFilan :
From: https://axrp.net/episode/2021/03/10/episode-5-infra-bayesianism-vanessa-kosoy.html
Perhaps this is a nice explanation for some people with mathematical or statistical knowledge, but alas it goes way over my head.
(Specifically, I get lost here: “ We just consider all probability distributions that predict that the odd bits will be zero with probability one, and without saying anything at all - the even bits, they can be anything.”)
(Granted, I now at least think I understand what a convex set is, although I fail to understand its relevance in this conversation.)
Fair point! Sorry it wasn't the most helpful. My attempt at explaining a bit more below:
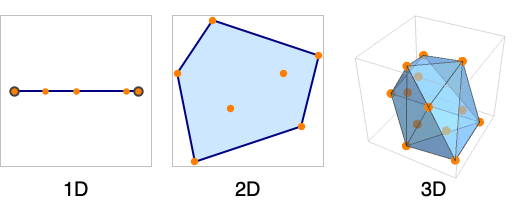
Convex sets are just sets where each point in the set can be expressed as weighted sum of the points on the exterior of the set, e.g.:
(source: https://reference.wolfram.com/language/ref/ConvexHullMesh.html)
In 1D, convex sets are just intervals, [a, b], and convex sets of probability distributions basically correspond to intervals of probability values, e.g. [0.1, 0.5], which are often called "imprecise probabilities".
Let's generalize this idea to 2D. There are two events, A and B, which I am uncertain about. If I were really confident, I could say that I think A happens with probability 0.2, and B happens with probability 0.8. But what if I feel so ignorant that I can't assign a probability to event B? That means I think P(B) could be any probability between [0.0, 1.0], while keeping P(A) = 0.2. So my joint probability distribution P(A, B) is somewhere within the line segment (0.2, 0.0) to (0.2, 1.0). Line segments are a convex set.
You can generalize this notion to infinite dimensions -- e.g. for a bit sequence of infinite length, specifying a complete probability distribution would require saying how probable each bit is likely to be equal to 1, conditioned on the values of all of the other bits. But we could instead only assign probabilities to the odd bits, not the even bits, and that would correspond to a convex set of probability distributions.
Hopefully that explains the convex set bit. The other part is why it's better to use convex sets. Well, one reason is that sometimes we might be unwilling to specify a probability distribution, because we know the true underlying process is uncomputable. This problem arises, for example, when an agent is trying to simulate itself. I* can never perfectly simulate a copy of myself within my mind, even probabilistically, because that leads to infinite regress -- this sort of paradox is related to the halting problem and Godel's incompleteness theorem.
In at least these cases it seems better to say "I don't know how to simulate this part of me", rather pretending I can assign a computable distribution to how I will behave. For example, if I don't know if I'm going to finish writing this comment in 5 minutes, I can assign it the imprecise probability [0.2, 1.0]. And then if I want to act safely, I just assume the worst case outcomes for the parts of me I don't know how to simulate, and act accordingly. This applies to other parts of the world I can't simulate as well -- the physical world (which contains me), or simply other agents I have reason to believe are smarter than me.
(*I'm using "I" here, but I really mean some model or computer that is capable of more precise simulation and prediction than humans are capable of.)
Does it make more sense to think about all probability distributions that offers a probability of 50% for rain tomorrow? If we say this represents our epistemic state, then we're saying something like "the probability of rain tomorrow is 50%, and we withhold judgement about rain on any other day".
It feels more natural, but I’m unclear what this example is trying to prove. It still reads to me like “if we think rain is 50% likely tomorrow then it makes sense to say rain is 50% likely tomorrow” (which I realize is presumably not what is meant, but it’s how it feels).
A friend of mine just mentioned to me that the following points could be useful in the context of this discussion.
What DMDU researchers are usually doing is to use uniform probability distributions for all parameters when exploring future scenarios. This approach allows for a more even exploration of the plausible space, rather than being overly concerned with subjective probabilities, which may lead to sampling some regions of input-output space less densely and potentially missing decision-relevant outcomes. The benefit of using uniform probability distributions is that it can help to avoid compounding uncertainties in a way that can lead to biased results. When you use a uniform distribution, you assume that all values are equally likely within the range of possible outcomes. This approach can help to ensure that your exploration of the future is more comprehensive and that you are not overlooking important possibilities. Of course, there may be cases where subjective probabilities are essential, such as when there is prior knowledge or data that strongly suggests certain outcomes are more likely than others. In such cases, I'd say that it may be appropriate to incorporate those probabilities into the model.
Also, this paper by James Derbyshire on probability-based versus plausibility-based scenarios might be very relevant. The underlying idea of plausibility-based scenarios is that any technically possible outcome of a model is plausible in the real world, regardless of its likelihood (given that the model has been well validated). This approach recognizes that complex systems, especially those with deep uncertainties, can produce unexpected outcomes that may not have been considered in a traditional probability-based approach. When making decisions under deep uncertainty, it's important to take seriously the range of technically possible but seemingly unlikely outcomes. This is where the precautionary principle comes in (which advocates for taking action to prevent harm even when there is uncertainty about the likelihood of that harm). By including these "fat tail" outcomes in our analysis, we are able to identify and prepare for potentially severe outcomes that may have significant consequences. Additionally, nonlinearities can further complicate the relationship between probability and plausibility. In some cases, even a small change in initial conditions or inputs can lead to drastic differences in the final outcome. By exploring the range of plausible outcomes rather than just the most likely outcomes, we can better understand the potential consequences of our decisions and be more prepared to mitigate risks and respond to unexpected events.
I hope that helps!
I’m not sure I disagree with any of this, and in fact if I understood correctly, the point about using uniform probability distributions is basically what I was suggesting: it seems like you can always put 1/n instead of a “?” which just breaks your model. I agree that sometimes it’s better to say “?” and break the model because you don’t always want to analyze complex things on autopilot through uncertainty (especially if there’s a concern that your audience will misinterpret your findings), but sometimes it is better to just say “we need to put something in, so let’s put 1/n and flag it for future analysis/revision.”
Yes, I think that in this sense, it fits rather well! :)
Also, some more philosophical analysis of approaches to decision-making under deep uncertainty in
Mogensen, A.L., Thorstad, D. Tough enough? Robust satisficing as a decision norm for long-term policy analysis. Synthese 200, 36 (2022). https://doi.org/10.1007/s11229-022-03566-5
This s a great paper! Thanks for sharing!
You mention that
Are there any papers, writeups, blog posts etc I can check out to see how these techniques are applied "in the wild"? I'd be especially interested in writeups that show how simpler methods yield results deficient in some way, and how this methodology's results don't have those deficiencies.
Great question! There are indeed plenty of papers using systems modeling and there are various papers using decision-making under deep uncertainty. It's not always a combination of both though.
With respect to systems modeling, it might be interesting to look into economics in particular. Traditional economic modeling techniques, such as equilibrium models have certain limitations when it comes to addressing complex economic problems. These limitations arise from the assumptions and simplifications that these models make, which can be inadequate for representing the intricacies of real-world economic systems. Some are mentioned in the post above (rationality and perfect information, homogeneity, static equilibrium, linearity, and additivity. Agent-based modeling offers a better fit for analyzing complex economic problems because it addresses many of the limitations of traditional models. In simple terms, in traditional economic modeling (equilibrium models and standard game theory), it is inherently impossible to account for actual market phenomena (e.g. the emergence of market psychology, price bubbles, let alone market crashes). The Santa Fe Institute has produced some very valuable work on this. I would recommend reading Foundations of complexity economics by W. Arthur Brian. Other books and papers of his are excellent as well.
Some papers using the methodology of decision-making under deep uncertainty (DMDU):
I hope that these pointers help a bit!
Strongly upvoted for such a comprehensive answer, thank you Max! You've given me a lot to chew on.