Summary

• I believe many in the effective altruism community, including me in the past, have at some point concluded that reducing the nearterm risk of human extinction is astronomically cost-effective. For this to hold, it has to increase the chance that the future has an astronomical value, which is what drives its expected value.
• Nevertheless, reducing the nearterm risk of human extinction only obviously makes worlds with close to 0 value less likely. It does not have to make ones with astronomical value significantly more likely. A priori, I would say the probability mass is moved to nearby worlds which are just slightly better than the ones where humans go extinct soon. Consequently, interventions reducing nearterm extinction risk need not be astronomically cost-effective.
• I wonder whether the conclusion that reducing the nearterm risk of human extinction is astronomically cost-effective may be explained by:
  • Authority bias, binary bias and scope neglect.
  • Little use of empirical evidence and detailed quantitative models to catch the above biases.

Why reducing the nearterm risk of human extinction might be astronomically cost-effective

I believe many in the effective altruism community, including me in the past, have at some point concluded that reducing the nearterm risk of human extinction is astronomically cost-effective. This follows from multiplying:

• A non-negligible reduction in the nearterm risk of human extinction per cost. By nearterm, I mean the next few decades.
• An astronomical expected value of the (longterm) future.

To illustrate, one would get a cost-effectiveness in terms of saving human lives of 3.04*10^39 life/$ (= 2.17*10^-13*1.40*10^52), considering:

• A reduction in the nearterm risk of human extinction of 2.17*10^-13 per dollar, which is the median cost-effectiveness bar for mitigating existential risk I collected.
  • The bar does not respect extinction risk, but I assume the people who provided the estimates would have guessed similar values for extinction risk.
  • I personally guess human extinction is very unlikely to be an existential catastrophe:
    • I estimated a 0.0513 % chance of not fully recovering from a repetition of the last mass extinction 66 M years ago, the Cretaceous–Paleogene extinction event.
    • If biological humans go extinct because of advanced AI, I guess it is very likely they will have suitable successors then, either in the form of advanced AI or some combinations between it and humans.
• An expected value of the future of 1.40*10^52 human lives (= (10^54 - 10^23)/ln(10^54/10^23)), which is the mean of a loguniform distribution with minimum and maximum of:
  • 10^23 human lives, which is the estimate for “an extremely conservative reader” obtained in Table 3 of Newberry 2021.
  • 10^54 lives, which is the largest estimate in Table 1 of Newberry 2021, determined for the case where all the resources of the affectable universe support digital persons. The upper bound can be 10^30 times as high if civilization “aestivate[s] until the far future in order to exploit the low temperature environment”, in which computations are more efficient. Using a higher bound does not qualitatively change my point.

Why it is not?

Firstly, I do not think reducing the nearterm risk of human extinction being astronomically cost-effective implies it is astronomically more cost-effective than interventions not explicitly focussing on tail risk, like ones in global health and development and animal welfare.

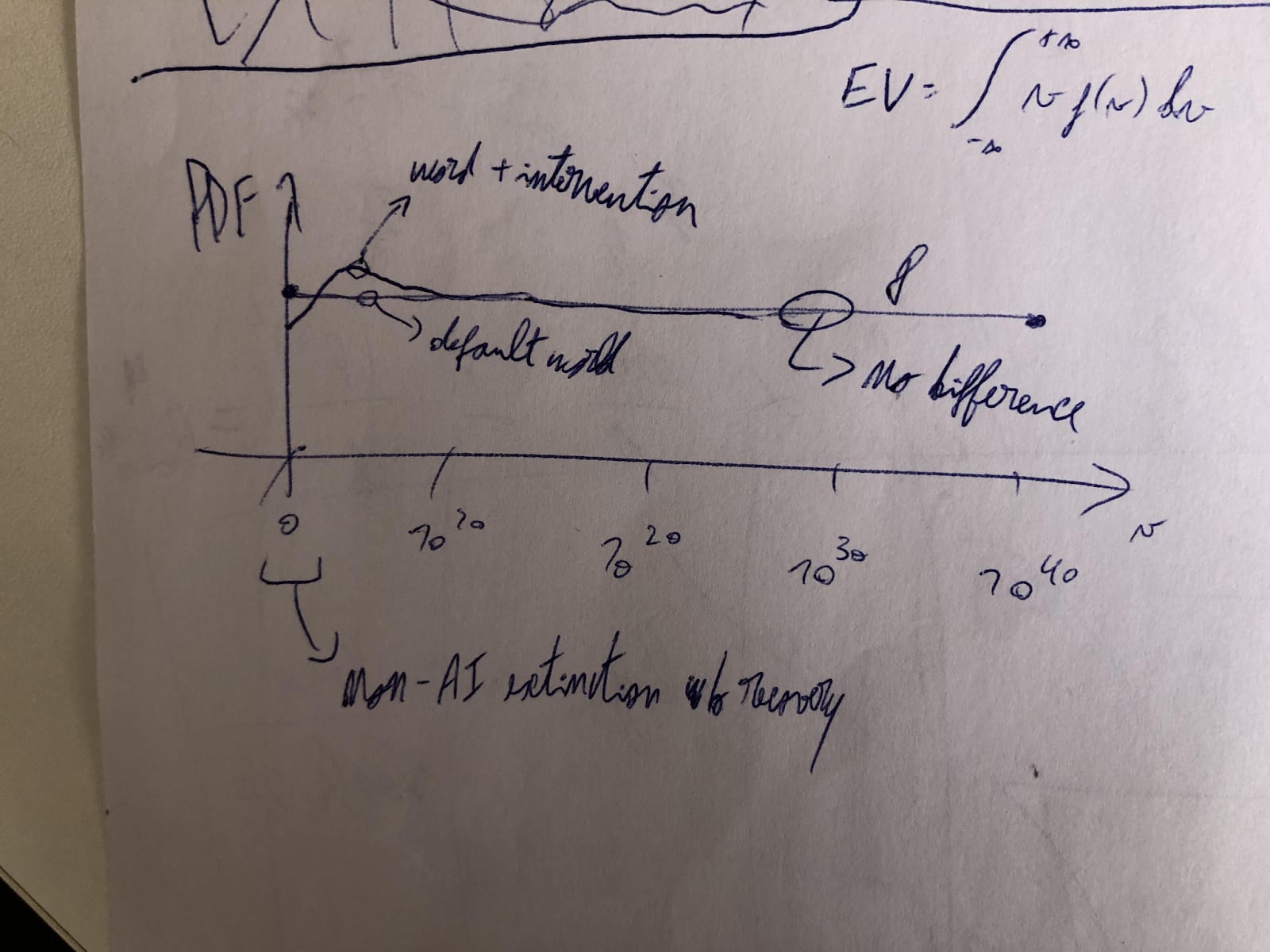
Secondly, and this is what I wanted to discuss here, calculations like the above crucially suppose the reduction in nearterm risk of human extinction is the same as the relative increase in the expected value of the future. For this to hold, reducing such risk has to increase the chance that the future has an astronomical value, which is what drives its expected value. Nevertheless, it only obviously makes worlds with close to 0 value less likely. It does not have to make ones with astronomical value significantly more likely. A priori, I would say the probability mass is moved to nearby worlds which are just slightly better than the ones where humans go extinct soon. Below is my rough sketch of the probability density functions (PDFs) of the value of the future in terms of human lives, before and after an intervention reducing the nearterm risk of human extinction^[1].

The expected value (EV) of the future is the integral of the product between the value of the future and its PDF. I assumed the value of the future follows a loguniform distribution from 1 to 10^40 human lives. In the worlds with the least value, humans go extinct soon without the involvement of AI, which has some welfare in expectation, and there is no recovery via the emergence of a similarly intelligent and sentient species^[2]. I am also not accounting for wild animals due to the high uncertainty about whether they have positive or negative lives.

In any case, the distribution I sketched does not correspond to my best guess, and I do not think the particular shape matters for the present discussion^[3]. What is relevant is that, for all cases, it makes sense to me that an intervention aiming to decrease (increase) the probability of a given set of worlds makes nearby similarly valuable worlds significantly more (less) likely, but super faraway worlds only infinitesimally more (less) so. As far as I can tell, the (posterior) counterfactual impact of interventions whose effects can be accurately measured, like ones in global health and development, decays to 0 as time goes by, and can be modelled as increasing the value of the world for a few years or decades, far from astronomically. Accordingly, I like that Rethink Priorities’ cross-cause cost-effectiveness model (CCM) assumes no counterfactual impact of existential risk interventions after the year of 3023, although I would rather assess interventions based on standard cost-effectiveness analyses.

In light of the above, I expect what David Thorstad calls rapid diminution. I see the difference between the PDF after and before an intervention reducing the nearterm risk of human extinction as quickly decaying to 0, thus making the increase in the expected value of the astronomically valuable worlds negligible. For instance:

• If the difference between the PDF after and before the intervention decays exponentially with the value of the future v, the increase in the value density caused by the intervention will be proportional to v*e^-v^[4].
• The above rapidly goes to 0 as v increases. For a value of the future equal to my expected value of 1.40*10^52 human lives, the increase in value density will multiply a factor of 1.40*10^52*e^(-1.40*10^52) = 10^(log10(1.40)*52 - log10(e)*1.40*10^52) = 10^(-6.08*10^51), i.e. it will be basically 0.

The increase in the expected value of the future equals the integral of the increase in value density. As illustrated just above, this increase can easily be negligible for astronomically valuable worlds. Consequently, interventions reducing the nearterm risk of human extinction need not be astronomically cost-effective, and I currently do not think they are.

Intuition pumps

Here are some intuition pumps for why reducing the nearterm risk of human extinction says practically nothing about changes to the expected value of the future. In terms of:

• Human life expectancy:
  • I have around 1 life of value left, whereas I calculated an expected value of the future of 1.40*10^52 lives.
  • Ensuring the future survives over 1 year, i.e. over 8*10^7 lives (= 8*10^(9 - 2)) for a lifespan of 100 years, is analogous to ensuring I survive over 5.71*10^-45 lives (= 8*10^7/(1.40*10^52)), i.e. over 1.80*10^-35 seconds (= 5.71*10^-45*10^2*365.25*86400).
  • Decreasing my risk of death over such an infinitesimal period of time says basically nothing about whether I have significantly extended my life expectancy. In addition, I should be a priori very sceptical about claims that the expected value of my life will be significantly determined over that period (e.g. because my risk of death is concentrated there).
  • Similarly, I am guessing decreasing the nearterm risk of human extinction says practically nothing about changes to the expected value of the future. Additionally, I should be a priori very sceptical about claims that the expected value of the future will be significantly determined over the next few decades (e.g. because we are in a time of perils).
• A missing pen:
  • If I leave my desk for 10 min, and a pen is missing when I come back, I should not assume the pen is equally likely to be in any 2 points inside a sphere of radius 180 M km (= 10*60*3*10^8) centred on my desk. Assuming the pen is around 180 M km away would be even less valid.
  • The probability of the pen being in my home will be much higher than outside it. The probability of being outside Portugal will be negligible, but the probability of being outside Europe even lower, and in Mars even lower still^[5].
  • Similarly, if an intervention makes the least valuable future worlds less likely, I should not assume the missing probability mass is as likely to be in slightly more valuable worlds as in astronomically valuable worlds. Assuming the probability mass is all moved to the astronomically valuable worlds would be even less valid.
• Moving mass:
  • For a given cost/effort, the amount of physical mass one can transfer from one point to another decreases with the distance between them. If the distance is sufficiently large, basically no mass can be transferred.
  • Similarly, the probability mass which is transferred from the least valuable worlds to more valuable ones decreases with the distance (in value) between them. If the world is sufficiently faraway (valuable), basically no mass can be transferred.

What do slightly more valuable worlds look like? If the nearterm risk of human extinction refers to the probability of having at least 1 human alive by e.g. 2050, a world slightly more valuable than one where humans go extinct before then would have the last human dying in 2050 instead of 2049, and having a net positive experience during the extra time alive. This is obviously not what people mean by reducing the nearterm risk of human extinction, but it also does not have to imply e.g. leveraging all the energy of the accessible universe to run digital simulations of super happy lives. There are many intermediate outcomes in between, and I expect the probability of the astronomically valuable ones to be increased only infinitesimally.

Similarities with arguments for the existence of God?

One might concede that reducing the nearterm risk of human extinction does not necessarily lead to a meaningful increase in the expected value of the future, but claim that reducing nearterm existential risk does so, because the whole point of existential risk reduction is that it permanently increases the expected value of the future. However, this would be begging the question. To avoid this, one has to present evidence supporting the existence of interventions with permanent effects instead of assuming (the conclusion that) they exist^[6], and correspond to the ones designated (e.g. by 80,000 Hours) as decreasing existential risk.

I cannot help notice arguments for reducing the nearterm risk of human extinction being astronomically cost-effective might share some similarities with (supposedly) logical arguments for the existence of God (e.g. Thomas Aquinas’ Five Ways), although they are different in many aspects too. Their conclusions seem to mostly follow from:

• Cognitive biases. In the case of the former, the following come to mind:
  • Authority bias. For example, in Existential Risk Prevention as Global Priority, Nick Bostrom interprets a reduction in (total/cumulative) existential risk as a relative increase in the expected value of the future, which is fine, but then deals with the former as being independent from the latter, which I would argue is misguided given the dependence between the value of the future and increase in its PDF. “The more technologically comprehensive estimate of 10^54 human brain-emulation subjective life-years (or 10^52 lives of ordinary length) makes the same point even more starkly. Even if we give this allegedly lower bound on the cumulative output potential of a technologically mature civilisation a mere 1 per cent chance of being correct, we find that the expected value of reducing existential risk by a mere one billionth of one billionth of one percentage point is worth a hundred billion times as much as a billion human lives”.
    • Nitpick. The maths just above is not right. Nick meant 10^21 (= 10^(52 - 2 - 2*9 - 2 - 9)) times as much just above, i.e. a thousand billion billion times, not a hundred billion times (10^11).
  • Binary bias. This can manifest in assuming the value of the future is not only binary, but also that interventions reducing the nearterm risk of human extinction mostly move probability mass from worlds with value close to 0 to ones which are astronomically valuable, as opposed to just slightly more valuable.
  • Scope neglect. I agree the expected value of the future is astronomical, but it is easy to overlook that the increase in the probability of the astronomically valuable worlds driving that expected value can be astronomically low too, thus making the increase in the expected value of the astronomically valuable worlds negligible (see my illustration above).
• Little use of empirical evidence and detailed quantitative models to catch the above biases. In the case of the former:
  • As far as I know, reductions in the nearterm risk of human extinction as well as its relationship with the relative increase in the expected value of the future are always directly guessed.

Acknowledgements

Thanks to Anonymous Person for a discussion which led me to write this post, and feedback on the draft.

1. ^{^}

    The area under each curve should be the same (although it is not in my drawing), and equal to 1. In addition, “word + intervention” was supposed to be “world + intervention”.

2. ^{^}

    I estimated there would only be a 0.0513 % chance of a repetition of the last mass extinction 66 M years ago, the Cretaceous–Paleogene extinction event, being existential.

3. ^{^}

    As a side note, I have wondered about how binary is the value of the future.

4. ^{^}

    By value density, I mean the product between the value of the future and its PDF.

5. ^{^}

    Mars’ aphelion 1.67 AU, and Earth’s is 1.02 AU, so Mars can be as much as 2.69 AU (= 1.67 + 1.02) away from Earth. This is more than the 1.20 AU (= 1.80*10^11/(1.50*10^11)) which the pen could have travelled at the speed of light. Consequently, the probability of it being in Mars could be as low as exactly 0 conditional on it not having travelled faster than light.

6. ^{^}

    As Toby Ord does in his framework for assessing changes to humanity’s longterm trajectory.

7. ^{^}

    Speculative side note. In theory, scope neglect might be a little explained by more extreme events being less likely. People may value a gain in welfare of 100 less than 100 times a gain of 1 because deep down they know the former is much less likely, and then fail to adequately account for the conditions of thought experiments where both deals are supposed to be equally likely. For a loguniform distribution, the value density does not depend on the value. For a Pareto distribution, it decreases with value, which could explain higher gains sometimes being valued less.