Summary

• Stephen Clare’s classic EA Forum post How likely is World War III? concludes “the chance of an extinction-level war [this century] is about 1%”. I commented that power law extrapolation often results in greatly overestimating tail risk, and that fitting a power law to all the data points instead of the ones in the right tail usually leads to higher risk too.
• To investigate the above, I looked into historical annual war deaths along the lines of what I did in Can a terrorist attack cause human extinction? Not on priors, where I concluded the probability of a terrorist attack causing human extinction is astronomically low.
• Historical annual war deaths of combatants suggest the annual probability of a war causing human extinction is astronomically low once again. 6.36*10^-14 according to my preferred estimate, although it is not resilient, and can easily be wrong by many orders of magnitude (OOMs).
• One may well update to a much higher extinction risk after accounting for inside view factors (e.g. weapon technology), and indirect effects of war, like increasing the likelihood of civilisational collapse. However, extraordinary evidence would be required to move up sufficiently many orders of magnitude for an AI, bio or nuclear war to have a decent chance of causing human extinction.
• In the realm of the more anthropogenic AI, bio and nuclear risk, I personally think underweighting the outside view is a major reason leading to overly high risk. I encourage readers to check David Thorstad’s series exaggerating the risks, which includes subseries on climate, AI and bio risk.

Introduction

The 166th EA Forum Digest had Stephen Clare’s How likely is World War III? as the classic EA Forum post (as a side note, the rubric is great!). It presents the following conclusions:

• First, I estimate that the chance of direct Great Power conflict this century is around 45%. 
• Second, I think the chance of a huge war as bad or worse than WWII is on the order of 10%.
• Third, I think the chance of an extinction-level war is about 1%. This is despite the fact that I put more credence in the hypothesis that war has become less likely in the post-WWII period than I do in the hypothesis that the risk of war has not changed.

I view the last of these as a crucial consideration for cause prioritisation, in the sense it directly informs the potential scale of the benefits of mitigating the risk from great power conflict. The 1 % chance of a war causing human extinction over a period of "77 years" results from assuming:

• With 35 % credence, an extinction risk per war of 0.06 %, and 1 war every 2 years ("constant risk hypothesis").
• With 65 % credence, an extinction risk per war of 0.03 %, and 1 war every 5 years ("durable peace hypothesis").

The extinction risk per war under the durable peace hypothesis is defined as half of that under the constant risk hypothesis^[1], and this is based on research from Bear Braumoeller (I recommend his appearance on The 80,000 Hours Podcast!). From How bad could a war get? by Stephen and Rani Martin:

“In Only the Dead, political scientist Bear Braumoeller uses his estimated parameters to infer the probability of enormous wars. His [power law] distribution gives a 1 in 200 chance of a given war escalating to be [at least] twice as bad as World War II and a 3 in 10,000 chance of it causing [at least] 8 billion deaths [of combatants] (i.e. human extinction).

I had already come across these posts, but now a 0.06 % chance of war causing human extinction based on historical data jumped out to me as more surprising. I had recently been looking into how astronomically unlikely it is for a terrorist attack to cause human extinction based on historical data.

So I commented on Stephen’s classic EA Forum post that:

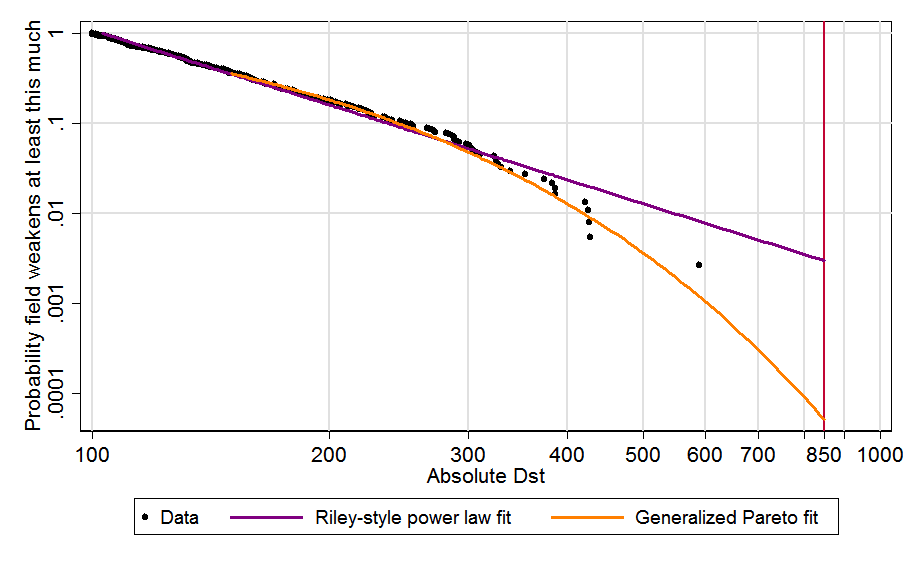
Power law extrapolation [the one used by Bear] often results in greatly overestimating tail risk because the tail usually starts decaying faster at some point. It is better to use a generalised Pareto distribution, which has the pareto distribution (power law) as a special case. David Roodman found using a generalised pareto instead of a power law led to a decrease in 2 orders of magnitude (OOMs) of the risk of a solar storm at least as severe as a Carrington event:

The Carrington event “was the most intense geomagnetic storm in recorded history”, but would very hardly cause extinction today (although now we have more electronics). As illustrated above, the higher the severity, the more the power law overestimates tail risk. So, if one fitted a generalised pareto to war deaths, I guess the extinction risk would decrease by many OOMs.

Another detail to have in mind is that, because the slope of the tail distribution usually bends downwards (as illustrated by the data points of the figure above), it matters whether we are fitting the power law to all the data points, or just to the right tail. The right tail will tend to have a more negative slope, so fitting a power law to all points will usually lead to overestimating the risk.

If one fitted a generalised pareto (instead of a power law) to e.g. 1 % or 10 % most deadly wars (instead of all wars), I guess the probability of a war causing human extinction would be OOMs lower than Bear’s 0.03 %. However, I expect it would still be many OOMs higher than my estimates for the extinction risk posed by terrorist attacks, as power laws still resulted in astronomically small risk of extinction (in agreement with Clauset 2013; see Figures 1 and 2). I might try to repeat the analysis for wars instead of terrorist attacks in the future, but you are welcome to do it yourself! Update: I will do it.

Aaron Clauset^[2] commented:

This [“the right tail will tend to have a more negative slope, so fitting a power law to all points will usually lead to overestimating the risk”] is not an accurate statement, in fact. The visual shape of the extreme upper tail is not a reliable indicator of the shape of the underlying generating distribution, because the extreme upper tail (where the largest events are) is the most subject to sampling fluctuations. Hence, in the case where the true data generating distribution is in fact power law, you will often still get an artifactual visual appearance of a somewhat negative slope. This is one reason why one has to use tail-fitting methods that have appropriate assumptions about the data generating process, or else you’re basically overfitting the data. Additionally, “right tail” is an ambiguous term -- where does the body end and the tail begin? There’s a set of methods designed to identify that point algorithmically, and generally speaking, visual methods (any methods like “Hill plots”) are highly unreliable for the reasons I mention at the beginning of this comment.

The above makes sense to me. Nevertheless, I maintain the actual tail distribution decaying faster is evidence that the underlying distribution has a thinner tail, although one should update less on this given the large amount of noise in the right tail. Moreover, our prior underlying distribution should eventually decay faster than a power law because this implies deaths can be arbitrarily large, whereas the real death toll is in fact limited to the global population. Noisier observations mean we should put greater weight on the prior, so one should end up with a thinner tail.

Methods

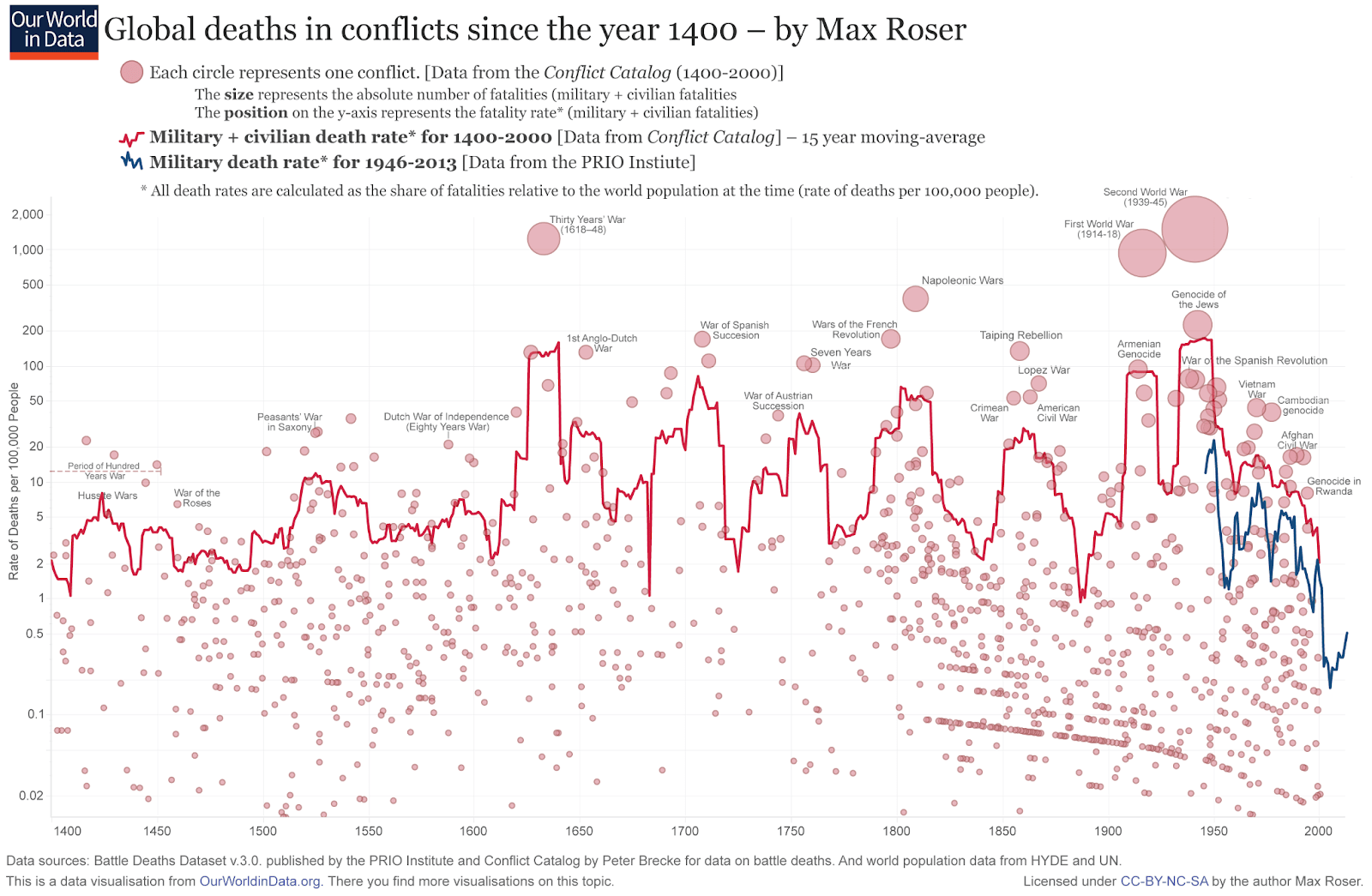
I used Correlates of War’s data on annual war deaths of combatants due to fighting, disease, and starvation. The dataset goes from 1816 to 2014, and excludes wars which caused less than 1 k deaths of combatants in a year.

Stephen commented I had better follow the typical approach of modelling war deaths, instead of annual war deaths as a fraction of the global population, and then getting the probability of human extinction from the chance of war deaths being at least as large as the global population. I think my approach is more appropriate, especially to estimate tail risk. There is human extinction if and only if annual war deaths as a fraction of the global population are at least 1. In contrast, war deaths as a fraction of the global population in the year the war started being at least 1 does not imply human extinction. Consider a war lasting for the next 100 years totalling 8 billion deaths. The war deaths as a fraction of the global population in the year the war started would be 100 %, which means such a war would imply human extinction under the typical approach. Nevertheless, this would only be the case if no humans were born in the next 100 years, and new births are not negligible. In fact, the global population increased thanks to these during the years with the most annual war deaths of combatants in the data I used:

• From 1914 to 1918 (years of World War 1), they were 9.28 M, 0.510 % (= 9.28/(1.82*10^3)) of the global population in 1914, but the global population increased 2.20 % (= 1.86/1.82 - 1) during this period.
• From 1939 to 1945 (years of World War 2), they were 17.8 M, 0.784 % (= 17.8/(2.27*10^3)) of the global population in 1939, but the global population increased 4.85 % (= 2.38/2.27 - 1) during this period.

I relied on the Python library fitter to find the distributions which best fit the top 10 % logarithm of the annual war deaths of combatants as a fraction of the global population. I only analysed the top 10 %, respecting more than 0.0153 % annual war deaths of combatants as a fraction of the global population, because I am interested in the right tail, which may decay faster than suggested by the whole distribution (see previous section). I took logarithms so that the probability density functions (PDFs) describing the actual data are defined based on points uniformly distributed in logarithmic space instead of linear space, which is appropriate given the wide variation of war deaths^[3].

fitter tries all the types of distributions in SciPy, 111 on 10 December 2023. For each type of distribution, the best fit is that with the lowest residual sum of squares (RSS), respecting the sum of the squared differences between the predicted and actual PDF. I set the number of bins to define the PDF to the square root of the number of data points^[4], and left the maximum time to find the best fit parameters to the default value in fitter of 30 s.

I estimated the probability of the annual war deaths as a fraction of the global population being at least 10^-6, 0.001 %, …, and 100 % (human extinction) as follows:

• I supposed deaths of combatants as a fraction of all deaths (f) are 10 %, 50 % (= 1/(1 + 1)) or 90 %. 50 % is my best guess following Stephen and Rani. “Historically, the ratio of civilian-deaths-to-battle deaths in war has been about 1-to-1 (though there’s a lot of variation across wars)”.
• I obtained the probability of the annual war deaths of combatants as a fraction of the global population being at least 10^-6 f, 0.001 % f, …, and f multiplying:
  • 10 %, which is the probability of the annual war deaths of combatants being in the right tail.
  • Probability of the annual war deaths of combatants as a fraction of the global population being at least 5*10^-7, 5*10^-6, …, and 50 % if they are in the right tail, which I got using the best fit parameters outputted by fitter.

I aggregated probabilities from different best fit distributions using the median. I did not use:

• The mean because it ignores information from extremely low predictions, and overweights outliers.
• The geometric mean of odds nor the geometric mean because many probabilities were 0.

The calculations are in this Sheet and this Colab.

Results

The results are in the Sheet.

Historical war deaths of combatants

Basic stats

Years by annual war deaths of combatants

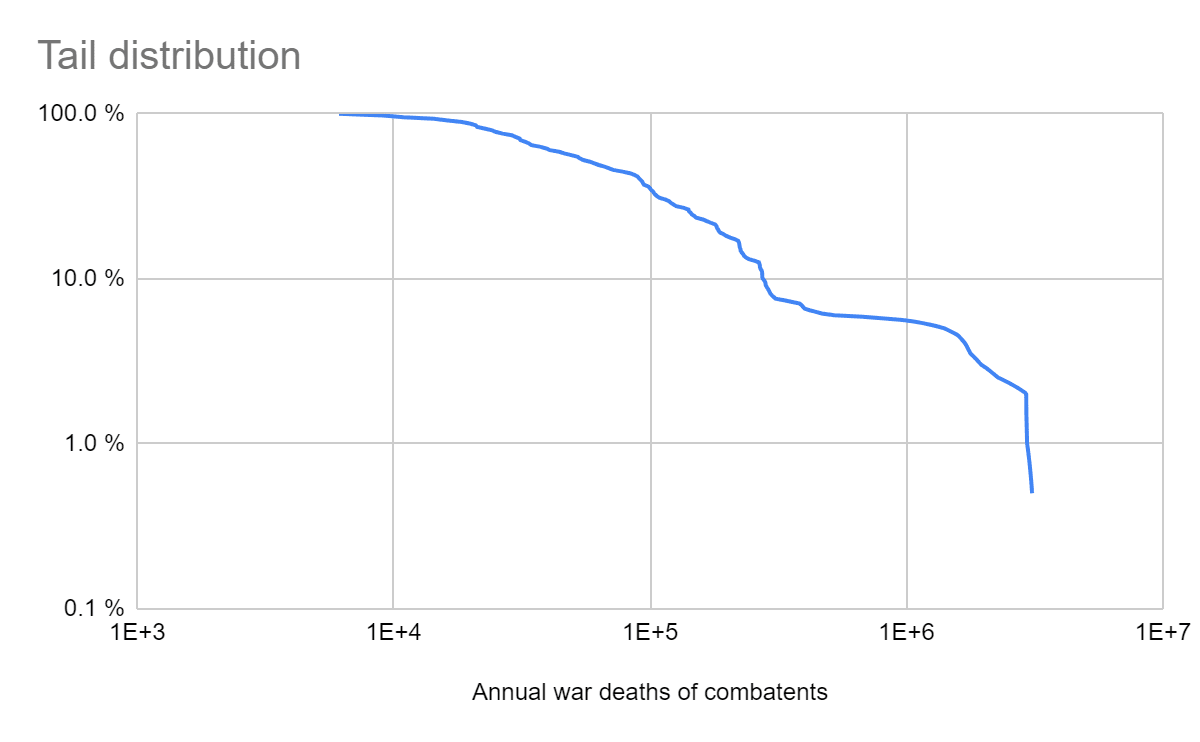
Tail distribution

War tail risk

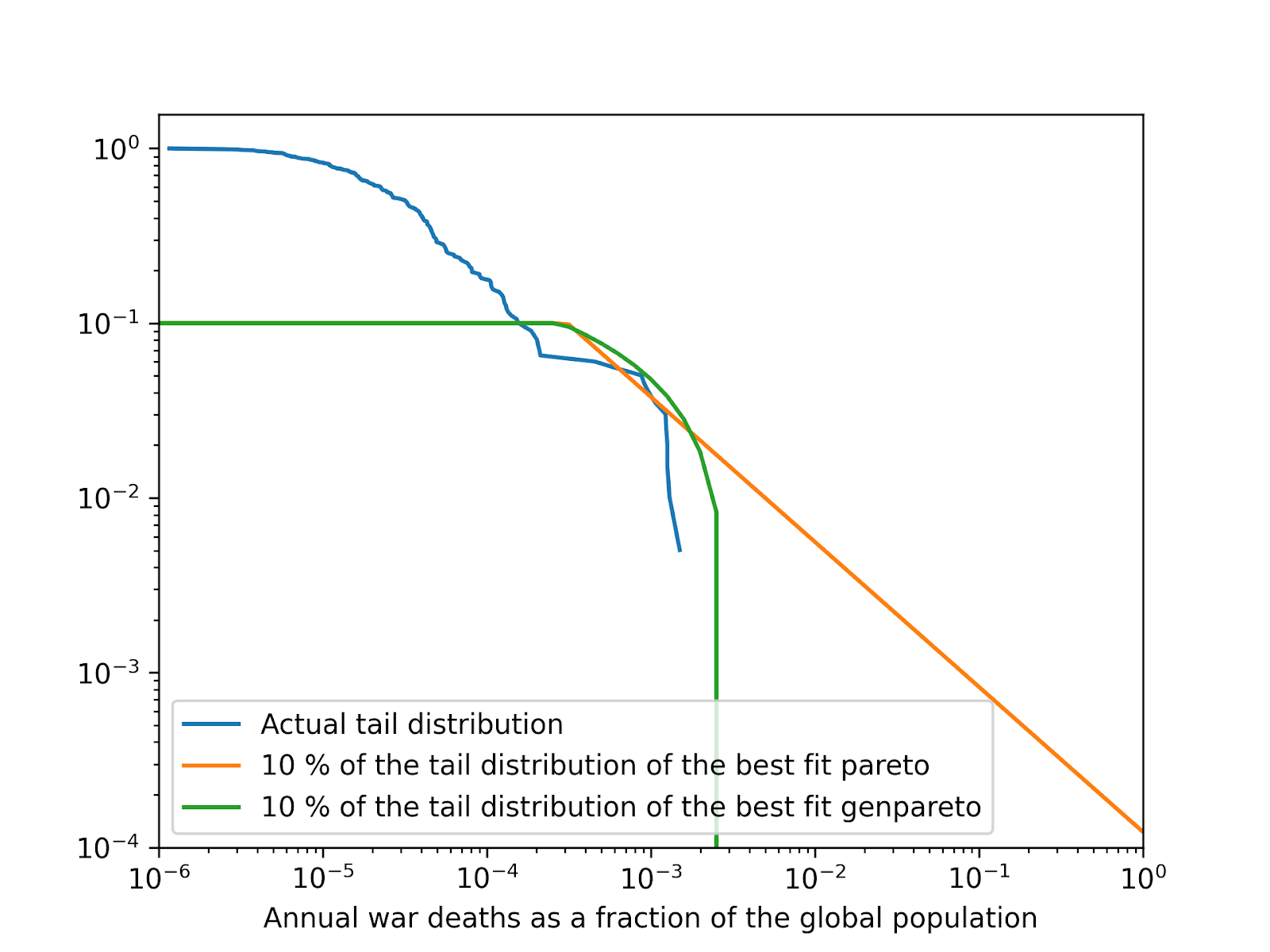
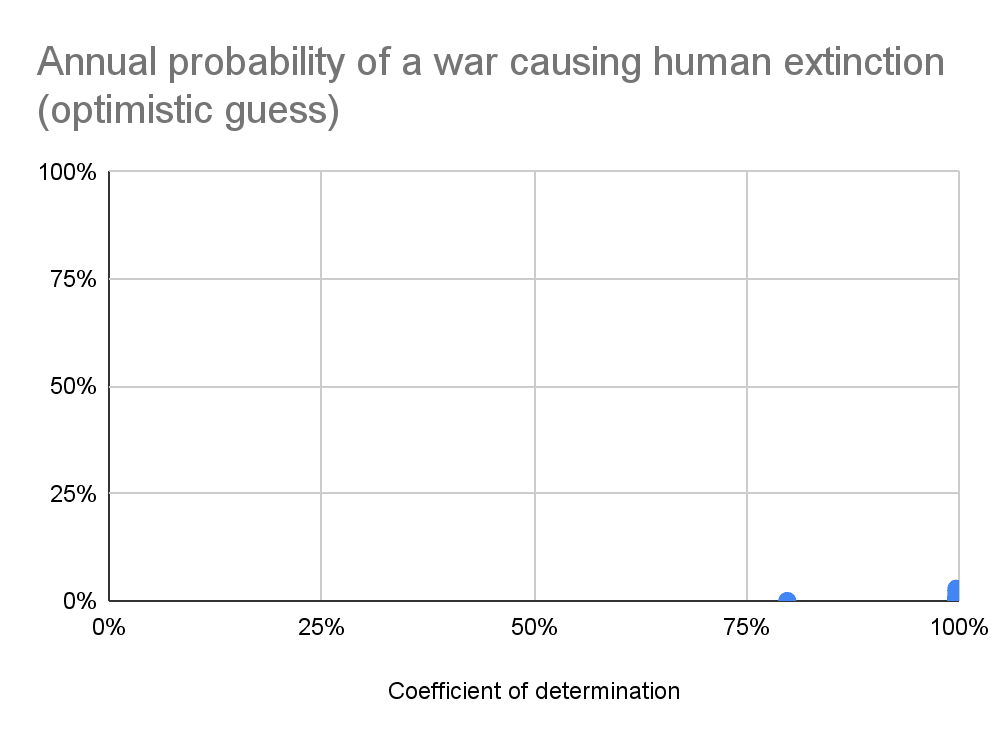
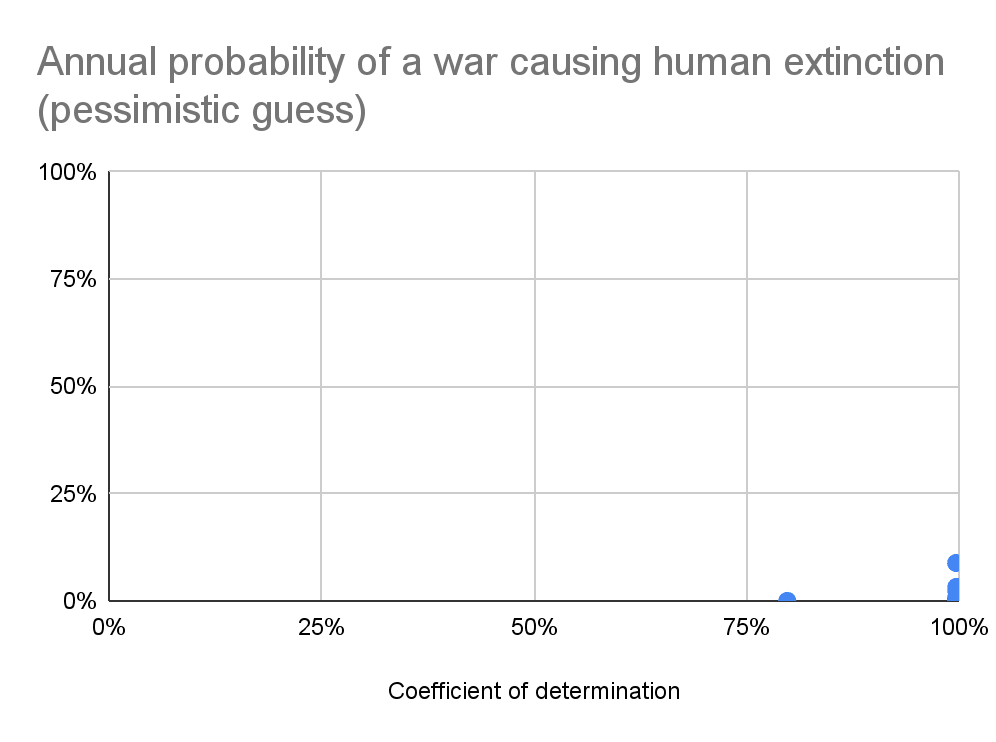
Below are the median RSS, coefficient of determination^[6] (R^2), and probability of the annual war deaths as a fraction of the global population being at least 10^-6, 0.001 %, …, and 100 % (human extinction). The medians are taken across the best, top 10, and top 100 distributions according to the default fitness criterion in fitter, lowest RSS^[7]. Null values may be exactly 0 if they concern bounded distributions, or just sufficiently small to be rounded to 0 due to finite precision. I also show the tail distribution of the actual data, and 10 % of the tail distributions of the best fit Pareto and generalised Pareto^[8], and the annual probability of a war causing human extinction as a function of R^2.

War deaths of combatants equal to 50 % of all deaths (best guess)

War deaths of combatants equal to 90 % of all deaths (optimistic guess)

War deaths of combatants equal to 10 % of all deaths (pessimistic guess)

Discussion

Historical annual war deaths of combatants suggest the annual probability of a war causing human extinction is astronomically low, with my estimates ranging from 0 to 9.02*10^-10. My preferred estimate is 6.36*10^-14, which belongs to the top 100 best fit distribution, and war deaths of combatants as a fraction of total deaths of 50 %. Among those with this value, it is the one which aggregates the most information, which is arguably good given the high median R^2 of 99.7 % of the top 100 best fit distributions.

As I expected, my methodology points to an extinction risk many orders of magnitude lower than Stephen’s. His war extinction risk of 0.95 % over 77 years corresponds to 0.0124 %/year (= 1 - (1 - 0.0095)^(1/77)), which is 9 (= log10(1.24*10^-4/(6.36*10^-14))) orders of magnitude above my best guess for the prior.

I do not think anthropics are confounding the results much. There would be no one to do this analysis if a war had caused human extinction in the past, but there would be for less severe wars, and there have not been any. The maximum annual war deaths of combatants as a fraction of the global population were only 0.150 %, which is still 2.52 (= -log10(0.00150/0.5)) orders of magnitude away from extinction.

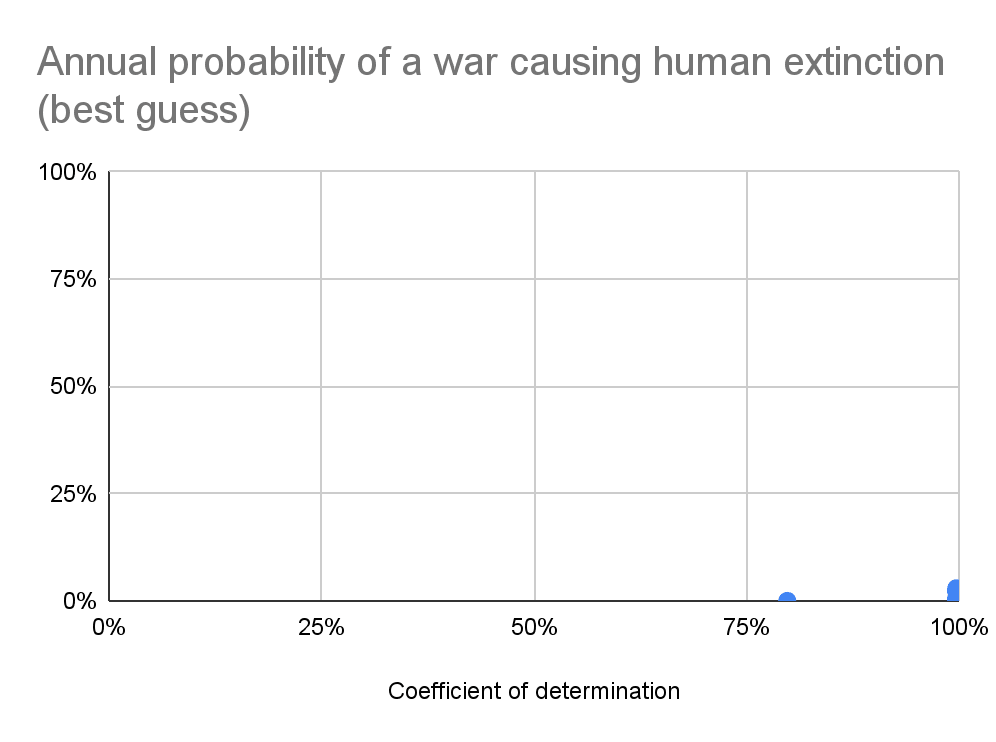
Interestingly, 102 best fit distributions have a R^2 of at least 99.7 %, but they result in annual probabilities of a war causing human extinction ranging from 0 to 15.7 %, with 5 respecting values higher than 1 % (see 1st graph in the previous section). As a consequence, figuring out which types of distributions should be weighted more heavily is a key consideration. Stephen noted investigating the connection between which distribution makes the most sense statistically and theoretically is missing in the literature on international relations, and that Bear was planning to work on this. Aaron commented “high R^2 values do not correlate with “good fits” of heavy tailed data, and other, more powerful and statistically grounded methods are required”, such as the ones discussed in Clauset 2009. It would be good to do a more in-depth analysis assessing distributions based on the best methods. Aaron elaborated that^[9]:

If you want to do this properly, you would want to first correctly assess which distributions are statistically plausible fits to the data [as in Clauset 2009], and then treat them as an ensemble, potentially bootstrapping their estimation in order to get a prior distribution of model parameters that you could use to estimate a posterior distribution for the probability of the event size you’re interested in. This would take some work, because this is a pretty esoteric task and quite different from the standard stuff that’s implemented in widely used stats packages.

Nonetheless, I do not think I have an a priori reason to put lots of weight into particular distributions with my current knowledge, so I assume it makes sense to rely on the median. Recall my preferred estimate stems from the results of the top 100 best fit distributions, thus not putting an unwarranted weight on ones which have a marginally higher R^2.

In addition, according to extreme value theory (EVT), the right tail should follow a generalised Pareto^[10], and the respective best fit distribution resulted in an extinction risk of exactly 0^[11] (R^2 of 99.8 %). Like I anticipated, the best fit Pareto (power law) resulted in a higher risk, 0.0122 % (R^2 of 99.7 %), i.e. 98.4 % (= 1.22*10^-4/(1.24*10^-4)) of Stephen’s 0.0124 %. Such remarkable agreement means the extinction risk for the best fit Pareto is essentially the same regardless of whether it is fitted to the top 10 % logarithm of the annual war deaths of combatants as a fraction of the global population (as I did), or to the war deaths of combatants per war (as implied by Stephen using Bear’s estimates). I guess this qualitatively generalises to other types of distributions. In any case, I would rather follow my approach.

In contrast, the type of distribution certainly matters. In the right tail domain of the actual data, ranging from 0.0153 % to 0.150 % annual war deaths of combatants as a fraction of the global population, the actual tail distribution, and 10 % of the tail distributions of the best fit Pareto and generalised Pareto are all similar (see 2nd graph in the previous section). Afterwards, kind of following the actual tail distribution, the generalised Pareto bends downwards much more than the Pareto, which implies a massive difference in their extinction risk. Aaron noted EVT’s “predictions only hold asymptotically [for infinitely many wars] and we have no way of assessing how close to “asymptopia” the current or extrapolated data might be”. I take this to mean it is unclear how much one should trust the best fit generalised Pareto, but a similar criticism applies to the best fit power law. It predicts deaths can be arbitrarily large, but they are in effect limited to the global population, so a power law will eventually cease to be a good model of the right tail at some point. In contrast, some of the best fit distributions I considered are bounded (e.g. the best generalised Pareto).

Aaron has looked into the trends and fluctuations in the severity of interstate wars in Clauset 2018, which also deals with the Correlates of War data. The article does not estimate the probability of a war causing human extinction, arguably given the limitations mentioned just above, but (like Stephen) used a power law^[12], did not restrict the analysis to the most deadly wars^[13] (although its model is tailored to accurately model the right tail), and focussed on war deaths rather than annual war deaths as a fraction of the global population^[14]. I have discussed why I consider all these 3 assumptions result in overestimating tail risk. Clauset 2018 did estimate a 50 % probability of a war causing 1 billion battle deaths^[15] in the next 1,339 years (see “The long view”), which is close to my pessimistic scenario:

• Assuming total war deaths are 2 times as large^[16], and that such a war lasts 6 years^[17], that death toll would correspond to annual deaths of 333 M (= 2*10^9/6), 4.21 % (= 0.333/7.91) of the global population in 2021.
• The 50 % probability would respect an annual chance of 0.0518 % (= 1 - (1 - 0.5)^(1/1339)).
• According to my pessimistic estimates, the chance of annual war deaths being at least as large as 1 % of the global population (about 1/4 the above 4.21 %) is 2.21 % to 3.36 % (about 4 times the above 0.0518 %).

There may be a temptation to guess something like a 10 % chance of human extinction if there is at least 1 billion battle deaths, in which case Aaron’s results would suggest an annual extinction risk due to war of 0.005 % (= 5.18*10^-4*0.1). Millett 2017 does a move like this, “assuming that only 10% of such [bio] attacks that kill more than 5 billion eventually lead to extinction (due to the breakdown of society, or other knock-on effects)”. In general, I suspect there is a tendency to give probabilities between 1 % and 99 % for events whose mechanics we do not understand well, given this range encompasses the vast majority (98 %) of the available linear space (from 0 to 1), and events in everyday life one cares about are not that extreme. However, the available logarithmic space is infinitely vast, so there is margin for such guesses to be major overestimates. In the context of tail risk, subjective guesses can easily fail to adequately account for the faster decay of the tail distribution as severity approaches the maximum.

As a final reflection, Aaron added that:

Based on everything I know from working in this field for 20 years, and having written several of the state-of-the-art papers in this broad area, my professional opinion is that these calculations are fun, but they are not science. They might be useful as elaborate statistical thought experiments, and perhaps useful for helping us think through other aspects of the underlying causes of war and war size, but no one should believe these estimates are accurate in the long run [or in the extreme right tail].

Well, Clauset 2018 was published in Science Advances, so I suppose it is fair to say such work is science, although I agree it is fun too. More seriously, I understand it is difficult to get reliable estimates of tail risk. If it is worth doing, it is worth doing with made-up statistics, and I did my analysis in this spirit, but none of my mainline estimates are resilient. My estimates of extinction risk can all easily be wrong by many OOMs. Yet, I hope they highlight there is much room for disagreement over predictions of high risk of human extinction due to a war this century, and ideally encourage further work.

I must also say one may well update to a much higher extinction risk after accounting for inside view factors (e.g. weapon technology), and indirect effects of war, like increasing the likelihood of civilisational collapse. However, extraordinary evidence would be required to move up sufficiently many orders of magnitude for an AI, bio or nuclear war to have a decent chance of causing human extinction. Moreover, although war-making capacity has been increasing, conflict deaths as a fraction of the global population have not changed much in the past 6 centuries (relatedly).

Stephen commented nuclear weapons could be an example of extraordinary evidence, and I somewhat agree. However:

• Nuclear risk has been decreasing. The estimated destroyable area by nuclear weapons deliverable in a first strike has decreased 89.2 % (= 1 - 65.2/601) since its peak in 1962.
• I think today’s nuclear risk is much lower than Stephen’s 1 % chance of a war causing human extinction this century. I estimated a probability of 3.29*10^-6 for a 50 % population loss due to the climatic effects of nuclear war before 2050, so around 0.001 % (= 3.29*10^-6*76/26) before 2100. I guess extinction would be much less likely, maybe 10^-7 this century. This is much lower than the forecasted in The Existential Risk Persuasion Tournament (XPT), which I have discussed before.

In general, I agree with David Thorstad that Toby Ord’s guesses for the existential risk between 2021 and 2120 given in The Precipice are very high (e.g. 0.1 % for nuclear war). In the realm of the more anthropogenic AI, bio and nuclear risk, I personally think underweighting the outside view is a major reason leading to overly high risk. I encourage readers to check David’s series exaggerating the risks, which includes subseries on climate, AI and bio risk. Relatedly, I commented before that:

David Thorstad’s posts, namely the ones on mistakes in the moral mathematics of existential risk, epistemics and exaggerating the risks, increased my general level of scepticism towards deferring to thought leaders in effective altruism before having engaged deeply with the arguments. It is not so much that I got to know knock-down arguments against existential risk mitigation, but more that I become more willing to investigate the claims being made.

Acknowledgements

Thanks to Aaron Clauset and Stephen Clare for feedback on the draft.

1. ^{^}

    I [Stephen] haven’t formally modeled this reduction. It’s based on my sense of the strength of the evidence on changing international norms and nuclear deterrence.

2. ^{^}

    Thanks to Stephen for prompting me to reach out to Aaron.

3. ^{^}

    The median fraction of explained variance across the 100 best fit distributions (highest fraction of explained variance) was 99.7 % defining the actual PDF based on points uniformly distributed in logarithmic space, but only 68.5 % based on points uniformly distributed in linear space.

4. ^{^}

    Setting the number of bins to the number of data points would result in overfitting.

5. ^{^}

    5 years for World War 1 (1914 to 1918), and 7 for World War 2 (1939 to 1945).

6. ^{^}

    Fraction of the variance of the actual PDF explained by the predicted PDF. I computed this fraction from 1 minus the ratio between the residual and total sum of squares.

7. ^{^}

    Equivalent to lowest R^2.

8. ^{^}

    I multiply the tail distributions of the best fit distributions by 10 % because they are supposed to model the right tail, and there is a 10 % chance of the annual war deaths being in the right tail as I defined it.

9. ^{^}

    Aaron additionally commented that:

   Even then, you have a deeper assumption that is quite questionable, which is whether events are plausibly iid [independent and identically distributed] over such a long time scale. This is where the deep theoretical understanding from the literature on war is useful, and in my 2018 paper [Clauset 2018], my Discussion section delves into the implications of that understanding for making such long term and large-size extrapolations.

   Assuming wars are IID over a long time scale would be problematic if one wanted to estimate the time until a war caused human extinction, but I do not think it is an issue to estimate the nearterm annual extinction risk.

10. ^{^}

     The exponential, uniform, Pareto and exponentiated generalised Pareto distributions are particular cases of the generalised Pareto distribution.

11. ^{^}

     The best fit generalised Pareto has a bounded domain because its shape parameter is negative.

12. ^{^}

     “The estimated power-law model has two parameters: $x_{min}$, which represents the smallest value above which the power-law pattern holds, and $\alpha$, the scaling parameter”.

13. ^{^}

     “All recorded interstate wars are considered”.

14. ^{^}

     “War variables are analyzed in their unnormalized forms”.

15. ^{^}

     I think battle deaths refer to all deaths of combatants, not only those due to fighting, but also disease and starvation, as these are all included in the Correlates of War dataset.

16. ^{^}

     Total deaths are 2 times the deaths of combatants in my best guess scenario.

17. ^{^}

     Mean between the durations of 5 (= 1918 - 1914 + 1) and 7 (= 1945 - 1939 + 1) years of World War 1 and 2.