Summary

Most moral impact estimates and cost-effectiveness analyses in the effective altruism community use (differences in) expected total welfare. However, doing so generally is probably irrational, based on arguments related to St Petersburg game-like prospects. These are prospects that are strictly better than each of their infinitely many possible but finite actual value outcomes, with unbounded but finite value across these outcomes. The arguments I consider here are:

1. Based on a money pump argument, the kind used to defend the axioms of expected utility theory, maximizing the expected value of an unbounded utility function is irrational. As a special case, expectational total utilitarianism, i.e. maximizing the expected value of total welfare, is also irrational.
2. Two recent impossibility theorems demonstrate the incompatibility of Stochastic Dominance — a widely accepted requirement for instrumental rationality — with Impartiality and each of Anteriority and Separability. These last three principles are extensions of standard assumptions used in theorems to prove utilitarianism, e.g. Anteriority in Harsanyi's theorem.

Taken together, utilitarianism is either irrational or the kinds of arguments used to support it in fact undermine it instead when generalized. However, this doesn't give us any positive arguments for any other specific views.

I conclude with a discussion of responses.

EDIT: I've rewritten the summary and the title, and made various other edits for clarity and to better motivate. The original title of this post was "Utilitarianism is irrational or self-undermining".

Basic terminology

By utilitarianism, I include basically all views that are impartial and additive in deterministic fixed finite population cases. Some such views may not be vulnerable to all of the objections here, but they apply to most such views I’ve come across, including total utilitarianism. These problems also apply to non-consequentialists using utilitarian axiologies.

To avoid confusion, I prefer the term welfare as what your moral/social/impersonal preferences and therefore what your utility function should take into account.^[1] In other words, your utility function can be a function of individuals’ welfare levels.

A prospect is a probability distribution over outcomes, e.g. over heads or tails from a coin toss, over possible futures, etc..

Motivation and outline

Many people in the effective altruism and rationality communities seem to be expectational total utilitarians or give substantial weight to expectational total utilitarianism. They take their utility function to just be total welfare across space and time, and so aim to maximize the expected value of total welfare (total individual utility), E[∑Ni=1ui]. Whether or not committed to expectational total utilitarianism, many in these communities also argue based on explicit estimates of differences in expected total welfare. Almost all impact and cost-effectiveness estimation in the communities is also done this way. These arguments and estimation procedures agree with and use expected total welfare, but if there are problems with expectational total utilitarianism in general, then there’s a problem with the argument form and we should worry about specific judgements using it.

And‌ there are problems.

Total welfare, and differences in total welfare between prospects, may be unbounded, even if it were definitely finite. We shouldn't be 100% certain of any specified upper bound on how long our actions will affect value in the future, or even for how long a moral patient can exist and aggregate welfare over their existence. By this, I mean that you can't propose some finite number K such that your impact must, with 100% probability, be at most K. K doesn't have to be a tight upper bound. Here are some arguments for this:

1. Given any proposed maximum value, we can always ask: isn't there at least some chance it could go on for 1 second more? Even if extremely tiny. By induction, we'll have to go past any K.^[2]
2. How would you justify your choice of K and 100% certainty in it? (Feel free to try, and I can try to poke holes in the argument.)
3. You shouldn't be 100% certain of anything, except maybe logical necessities and/or some exceptions with continuous distributions (Cromwell's rule).
4. If you grant any weight to the views of those who aren't 100% sure of any specific finite upper bound, then you also shouldn't be 100% sure of any, either. If you don't grant any weight to them, then this is objectionably epistemically arrogant. For a defense of epistemic modesty, see Lewis, 2017.
5. There are some specific possibilities allowing this that aren't ruled out by models of the universe consistent with current observations, like creating more universes, from which other universes can be created, and so on (Tomasik, 2017).

We could also have no sure upper bound on the spatial size of the universe or the number of moral patients around now.^[3] Now, you might say you can just ignore everything far enough away, because you won't affect it. If your decisions don't depend on what's far enough away and unaffected by your actions, then this means, by definition, satisfying a principle of Separability. But then you're forced to give up impartiality or one of the least controversial proposed requirements of rationality, Stochastic Dominance. I'll state and illustrate these definitions and restate the result later, in the section Anti-utilitarian theorems.

This post is concerned with the implications of prospects with infinitely many possible outcomes and unbounded but finite value, not actual infinities, infinite populations or infinite ethics generally. The problems arise due to St Petersburg-like prospects or heavy-tailed distributions (and generalizations^[4]): prospects with infinitely many possible outcomes, infinite (or undefined) expected utility, but finite utility in each possible outcome. The requirements of rationality should apply to choices involving such possibilities, even if remote.

The papers I focus on are:

1. Jeffrey Sanford Russell, and Yoaav Isaacs. “Infinite Prospects*.” Philosophy and Phenomenological Research, vol. 103, no. 1, Wiley, July 2020, pp. 178–98, https://doi.org/10.1111/phpr.12704, https://philarchive.org/rec/RUSINP-2
2. ‌Goodsell, Zachary. “A St Petersburg Paradox for Risky Welfare Aggregation.” Analysis, vol. 81, no. 3, Oxford University Press, May 2021, pp. 420–26, https://doi.org/10.1093/analys/anaa079, https://philpapers.org/rec/GOOASP-2
3. Jeffrey Sanford Russell. “On Two Arguments for Fanaticism.” Noûs, Wiley-Blackwell, June 2023, https://doi.org/10.1111/nous.12461, https://philpapers.org/rec/RUSOTA-2, https://globalprioritiesinstitute.org/on-two-arguments-for-fanaticism-jeff-sanford-russell-university-of-southern-california/

Respectively, they:

1. Argue that unbounded utility functions (and generalizations) are irrational (or at least as irrational as violating Independence or the Sure-Thing Principle, crucial principles for expected utility theory).
2. Prove that Stochastic Dominance, Impartiality and Anteriority are jointly inconsistent.
3. Prove that Stochastic Dominance, Compensation (which implies Impartiality) and Separability are jointly inconsistent.

Again, respecting Stochastic Dominance is among the least controversial proposed requirements of instrumental rationality. Impartiality, Anteriority and Separability are principles (or similarly motivated extensions thereof) used to support and even prove utilitarianism.

I will explain what these results mean, including a money pump for 1 in the correspondingly named section, and definitions, motivation and background for the other two in the section Anti-utilitarian theorems. I won't include proofs for 2 or 3; see the papers instead. Along the way, I will argue based on them that all (or most standard) forms of utilitarianism are irrational, or the standard arguments used in defense of principles in support of utilitarianism actually extend to principles that undermine utilitarianism. Then, in the last section, Responses, I consider some responses and respond to them.

Unbounded utility functions are irrational

Expected utility maximization with an unbounded utility function is probably (instrumentally) irrational, because it recommends, in some hypothetical scenarios, choices leading to apparently irrational behaviour. This includes foreseeable sure losses — a money pump —, and paying to avoid information, among others, following from the violation of extensions of the Independence axiom^[5] and Sure-Thing Principle^[6] (Russell and Isaacs, 2021, p.3-5).^[7] The issue comes from St Petersburg game-like prospects: prospects with infinitely many possible outcomes, each of finite utility, but with overall infinite (or undefined) expected utility, as well as generalizations of such prospects.^[4] Such a prospect is, counterintuitively, better than each of its possible outcomes.^[8]

The original St Petersburg game is a prospect that with probability 1/2n gives you $2n, for each positive integer n (Peterson, 2023). The expected payout from this game is infinite,^[9] even though each possible outcome is finite. But it's not money we care about in itself.

Suppose you have an unbounded real-valued utility function u.^[4] Then it’s unbounded above or below. Assume it’s unbounded above, as a symmetric argument applies if it’s only unbounded below. Then, being unbounded above implies that it takes some utility value u(x)>0, and for each utility value u(x)>0, there’s some outcome x′ such that u(x′)≥2u(x). Then we can construct a countable sequence of outcomes, x1,x2,…,xn, with u(xn+1)≥2u(xn) for each n>1, as follows:

1. Choose an outcome x1 such that u(x1)>0.
2. Choose an outcome x2 such that u(x2)≥2u(x1).
3. …
4. Choose an outcome xn+1 such that u(xn+1)≥2u(xn).
5. …

Define a prospect X as follows: with probability 1/2n,X=xn. Then, E[u(X)]=∞,^[10] and X is better than any prospect with finite expected utility.^[11]

St Petersburg game-like prospects lead to violations of generalizations of the Independence axiom and the Sure-Thing Principle to prospects over infinitely (countably) many possible outcomes (Russell and Isaacs, 2021).^[12] The corresponding standard finitary versions are foundational principles used to establish expected utility representations of preferences in the von Neumann-Morgenstern utility theorem (von Neumann and Morgenstern, 1944) and Savage’s theorem (Savage, 1972), respectively. The arguments for the countable generalizations are essentially the same as those for the standard finitary versions (Russell and Isaacs, 2021), and in the following subsection, I will illustrate one: a money pump argument. So, if money pumps establish the irrationality of violations of the standard finitary Sure-Thing Principle, they should too for the countable version. Then maximizing the expected value of an unbounded utility function is irrational.

A money pump argument

Consider the following hypothetical situation, adapted from Russell and Isaacs, 2021, but with a genie instead. It’s the same kind of money pump that would be used in support of the Sure-Thing Principle, and structurally nearly identical to the one to used to defend Independence in Gustafsson, 2022.

You are facing a prospect A with infinite expected utility, but finite utility no matter what actually happens. Maybe A is your own future and you value your years of life linearly, and could live arbitrarily but finitely long, and so long under some possibilities that your life expectancy and corresponding expected utility is infinite. Or, you're an expectational total utilitarian, and thinking about the value in distant parts of the universe (or multiverse), with infinite expected value but almost certainly finite.^[13]

Now, there’s an honest and accurate genie — or God or whoever’s simulating our world or an AI with extremely advanced predictive capabilities — that offers to tell you exactly how A will turn out.^[14] Talking to them and finding out won’t affect A or its utility, they’ll just tell you what you’ll get. The genie will pester you unless you listen or you pay them $50 to go away. Since there’s no harm in finding out, and no matter what happens, being an extra $50 poorer is worse, because that $50 could be used for ice cream or bed nets,^[15] you conclude it's better to find out.

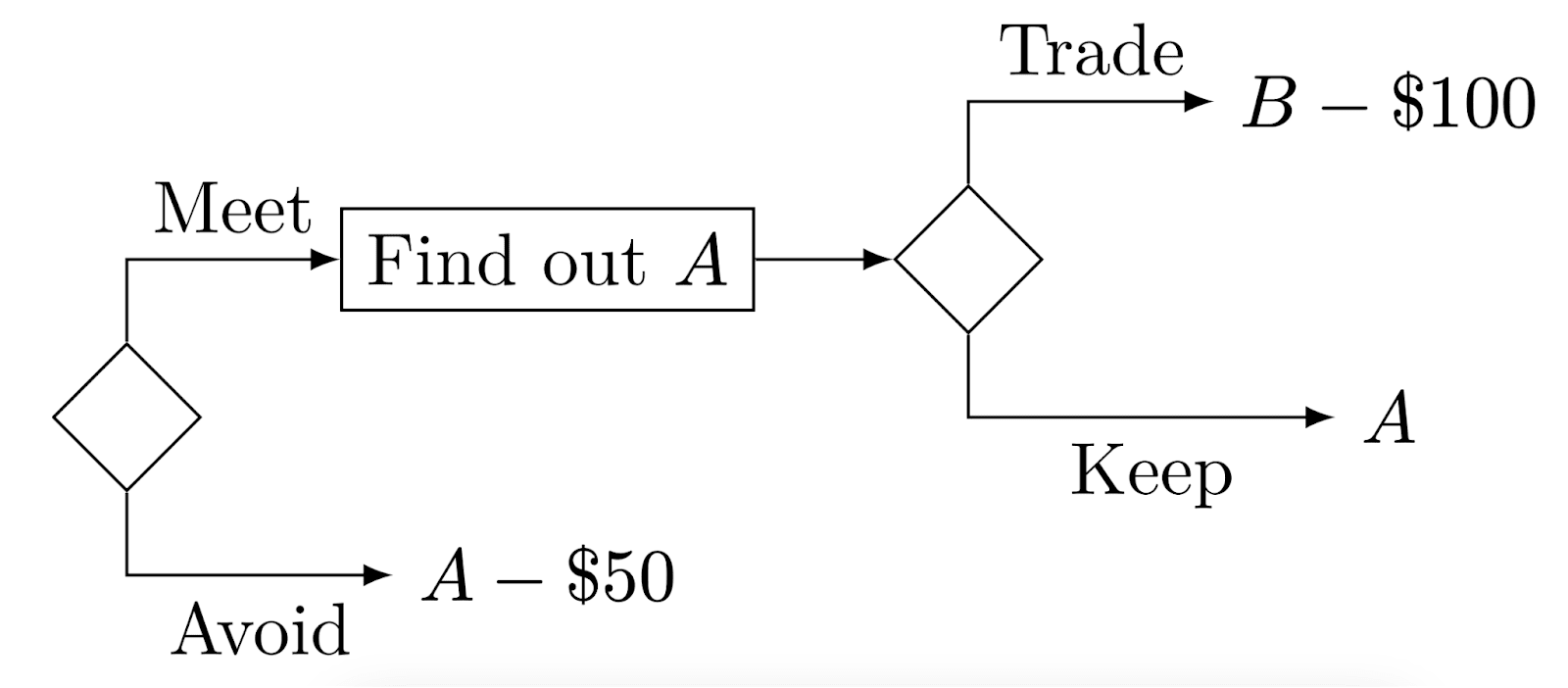
However, once you do find out, the result is, as you were certain it would be, finite. The genie turns out to be very powerful, too, and feeling generous, offers you the option to metaphorically reroll the dice. You can trade the outcome of A for a new prospect B with the same distribution as you had for A from before you found out, but statistically independent from the outcome of A. B would have been equivalent, because the distributions would have been the same, but B now looks better because the outcome of A is only finite. But, you’d have to pay the genie $100 for B. Still, $100 isn’t enough to drop the expected utility into the finite, and this infinite expected utility is much better than the finite utility outcome of A. You could refuse, but it's a worthwhile trade to make, so you do it.

But then you step back and consider what you've just done. If you hadn't found out the value of A, you would have stuck with it, since A was better than B - $100 ahead of time: A was equivalent to a prospect, the prospect B, that's certainly better than B - $100. You would have traded the outcome of A away for B - $100 no matter what the outcome of A would be, even though A was better ahead of time than B - $100. It was equivalent to B, and B - $100 is strictly worse, because it's the same but $100 poorer no matter what.

Not only that, if you hadn't found out the value of A, you would have no reason to pay for B. Even A - $50 would have been better than B - $100. Ahead of time, if you knew what the genie was going to do, but not the value of A, ending up with B - $100 would be worse than each of A and A - $50.

Suppose you're back at the start before knowing A and with the genie pestering you to hear how it will turn out. Suppose you also know ahead of time that the genie will offer you B for $100 no matter the outcome of A, but you don't yet know how A will turn out. Predicting what you'd do to respect your own preferences, you reason that if you find out A, no matter what it is, you'd pay $100 for B. In other words, accepting the genie's offer to find out A actually means ending up with B - $100 no matter what. So, really, accepting to find out A from the genie just is B - $100. But B - $100 is also worse than A - $50 (you're guaranteed to be $50 poorer than with B - $50, which is equivalent to A - $50). It would have been better to pay the genie $50 to go away without telling you how A will go.

So this time, you pay the genie $50 to go away, to avoid finding out true information and making a foreseeably worse decision based on it. And now you're out $50, and definitely worse off than if you could have stuck through with A, finding out its value and refusing to pay $100 to switch to B. And you had the option to stick with A though the whole sequence and could have, if only you wouldn't trade it away for B at a cost of $100.

So, whatever strategy you follow, if constrained within the options I described, you will act irrationally. Specifically, either

1. With nonzero probability, you will refuse to follow your own preferences when offered B - $100 after finding out A, which would be irrational then (Gustafsson, 2022 and Russell and Isaacs, 2021 argue similarly against resolute choice strategies). Or,
2. You pay the genie $50 at the start, leaving you with a prospect that’s certainly worse than one you could have ended up with, i.e. A without paying, and so irrational. This also looks like paying $50 to not find out A.

You're forced to act irrationally either way.

Anti-utilitarian theorems

Harsanyi, 1955 proved that our social (or moral or impersonal) preferences over prospects should be to maximize the expected value of a weighted sum of individual utilities in fixed population cases, assuming our social preferences and each individual’s preferences (or betterness) satisfy the standard axioms of expected utility theory and assuming our social preferences satisfy Ex Ante Pareto. Ex Ante Pareto is defined as follows: if between two options, A and B, everyone is at least as well off ex ante — i.e. A is at least as good as B for each individual —, then A⪰B according to our social preferences. Under these assumptions, according to the theorem, each individual in the fixed population has a utility function, ui, and our social preferences over prospects for each fixed population can be represented by the expected value of a utility function, this function equal to a linear combination of these individual utility functions, ∑Ni=1aiui. In other words,

A⪰B if and only if E[∑Ni=1aiui(A)]≥E[∑Ni=1ui(B)].

Now, if each individual’s utility function in a fixed finite population is bounded, then our social welfare function for that population, from Harsanyi’s theorem, would also be bounded. One might expect the combination of total utilitarianism and Harsanyi’s theorem to support expectational total utilitarianism.^[16] However, either the axioms themselves (e.g. the continuity/Archimedean axiom, or general versions of Independence or the Sure-Thing Principle) rule out expectational total utilitarianism, or the kinds of arguments used to defend the axioms (Russell and Isaacs, 2021). For example, essentially the same money pump argument, as we just saw, can be made against it. So, in fact, rather than supporting total utilitarianism, the arguments supporting the axioms of Harsanyi’s theorem refute total utilitarianism.

Perhaps you’re unconvinced by money pump arguments (e.g. Halstead, 2015) or expected utility theory in general. Harsanyi’s theorem has since been generalized in multiple ways. Recent results, without relying on the Independence axiom or Sure-Thing Principle at all, effectively obtain expectational utilitarianism in finite population cases or views including it as a special case, and with some further assumptions, expectational total utilitarianism specifically (McCarthy et al., 2020, sections 4.3 and 5 of Thomas, 2022, Gustafsson et al., 2023). They therefore don’t depend on support from money pump arguments either. In deterministic finite population cases and principles constrained to those cases, arguments based on Separability have also been used to support utilitarianism or otherwise additive social welfare functions (e.g. Theorem 3 of Blackorby et al., 2002 and section 5 of Thomas, 2022). So, there are independent arguments for utilitarianism, other than Harsanyi's original theorem.

However, recent impossibility results undermine them all, too. Given a preorder over prospects^[17]:

1. Goodsell, 2021 shows Stochastic Dominance, Anteriority and Impartiality are jointly inconsistent. This follows from certain St Petersburg game-like prospects over the population size but constant welfare levels. It also requires an additional weak assumption that most impartial axiologies I’ve come across satisfy^[18]: there's some finite population of equal welfare such that adding two more people with the same welfare is either strictly better or strictly worse. For example, if everyone has a hellish life, adding two more people with equally hellish lives should make things worse.
2. Russell, 2023 (Theorem 4) shows “Stochastic Dominance, Separability, and Compensation are jointly inconsistent”. As a corollary, Stochastic Dominance, Separability and Impartiality are jointly inconsistent, because Impartiality implies Compensation.

Russell, 2023 has some other impossibility results of interest, but I’ll focus on Theorem 4. I will define and motivate the remaining conditions here. See the papers for the proofs, which are short but technical.

Stochastic Dominance is generally considered to be a requirement of instrumental rationality, and it is a combination of two fairly obvious principles, Stochastic Equivalence and Statewise Dominance (e.g. Tarsney, 2020, Russell, 2023^[19]). Stochastic Equivalence requires us to treat two prospects as equivalent if for each set of outcomes, the two prospects are equally likely to have their outcome in that set, and we call such prospects stochastically equivalent. For example, if I win $10 if a coin lands heads, and lose $10 if it lands tails, that should be equivalent to me to winning $10 on tails and losing $10 on heads, with a perfectly 50-50 coin. It shouldn’t matter how the probabilities are arranged, as long as each outcome occurs with the same probability. Statewise Dominance requires us to treat a prospect A as at least as good as B if A is at least as good as B with probability 1, and we’d say A statewise dominates B in that case.^[20] It further requires us to treat A as strictly better than B, if on top of being at least as good as B with probability 1, A is strictly better than B with some positive probability, and in this case A strictly statewise dominates B. Informally, A statewise dominates B if A is always at least as good as B, and A strictly statewise dominates B if on top of that, A can also be better than B.

If instrumental rationality requires anything at all, it’s hard to deny that it requires respecting Stochastic Equivalence and Statewise Dominance. And, you respect Stochastic Dominance if and only if you respect both Stochastic Equivalence and Statewise Dominance, assuming transitivity. We’ll say A stochastically dominates B if there are prospects A′ and B′ to which A and Bare respectively stochastically equivalent and such that A′ statewise dominates B′ (we can in general take A′=A or B′=B, but not both), and A strictly stochastically dominates B if there are such A′ and B′ such that A′ strictly statewise dominates B′.

Impartiality can be stated in multiple equivalent ways for outcomes (deterministic cases) in finite populations:

1. only the distribution of welfares — the number of individuals at each welfare level (or lifetime welfare profiles) — matter in a population matter, not who realizes them or where or when they are realized, or
2. we can replace in an individual in any outcome with another individual at the same welfare level (or lifetime welfare profile), and the two outcomes will be equivalent.

Compensation is roughly the principle “that we can always compensate somehow for making things worse nearby, by making things sufficiently better far away (and vice versa)” (Russell, 2023). It is satisfied pretty generally by theories that are impartial in deterministic finite cases, including total utilitarianism, average utilitarianism, variable value theories, prioritarianism, critical-level utilitarianism, egalitarianism and even person-affecting versions of any of these views. In particular, theoretically “moving” everyone to nearby or “moving” everyone to far away without changing their welfare levels suffices.

Anteriority is a weaker version of Ex Ante Pareto: our social preferences are indifferent between two prospects whenever each individual is indifferent. The version Goodsell, 2021 uses, however, is stronger than typical statements of Anteriority and requires its application across different number cases:

If each possible person is equally likely to exist in either of two prospects, and for each welfare level, each person is, conditional on their existence, equally likely to have a life at least that good on either prospect, then those prospects are equally good overall.

This version is satisfied by expectational total utilitarianism, at least when the sizes of the populations in the prospects being compared are bounded by some finite number.

Separability is roughly the condition that parts of the world unaffected in a choice between two prospects can be ignored for ranking those prospects. What’s better or permissible shouldn’t depend on how things went or go for those unaffected by the decision.^[21] Or, following Russell, 2023, what we should do that only affects what’s happening nearby (in time and space) shouldn’t depend on what’s happening far away. In particular, in support of Separability and initially raised against average utilitarianism, there’s the Egyptology objection: the study of ancient Egypt and the welfare of ancient Egyptians “cannot be relevant to our decision whether to have children” (Parfit 1984, p. 420).^[22]

Separability can be defined as follows: for all prospects X, Y and B concerning outcomes for entirely separate things from both X and Y,

X⪰Y if and only if X⊕B⪰Y⊕B,

where ⊕ means combining or concatenating the prospects. For example, B could be the welfare of ancient Egyptians, while X and Y are the welfare of people today; the two may not be statistically independent, but they are separate, concerning disjoint sets of people and welfare levels. Average utilitarianism, many variable value theories and versions of egalitarianism are incompatible with Separability.

Separability is closely related to Anteriority and Ex Ante Pareto. Of course, Harsanyi’s theorem establishes Separability based on Ex Ante Pareto (or Anteriority) and axioms of Expected Utility Theory in fixed finite population cases, but we don’t need all of Expected Utility Theory. Separability, or at least in a subset of cases, follows from Anteriority (or Ex Ante Pareto) and some other modest assumptions, e.g. section 4.3 in Thomas, 2022. On the other hand, a preorder satisfying Separability, and in one-person cases, Anteriority or Ex Ante Pareto, will also satisfy Anteriority or Ex Ante Pareto, respectively, in fixed finite population cases.

So, based on the two theorems, if we assume Stochastic Dominance and Impartiality,^[23] then we can’t have Anteriority (unless it’s not worse to add more people to hell) or Separability. Anteriority and Separability are principles used to support utilitarianism, or at least natural generalizations of them defensible by essentially the same arguments. This substantially undermines all arguments for utilitarianism based on these principles. And my impression is that there aren’t really any other good arguments for utilitarianism, but I welcome readers to point any out!

Summary so far

To summarize the arguments so far (given some basic assumptions):

1. Unbounded utility functions and expectational total utilitarianism in particular are irrational because of essentially the same arguments as those used to support expected utility theory in the first place, including money pumps.
2. All plausible views either give up an even more basic requirement of rationality, Stochastic Dominance, or one of two other principles — or natural extensions that can be motivated the same way — used to defend utilitarianism, i.e. Impartiality or Anteriority.
3. All plausible views either give up Stochastic Dominance, or one of two other principles — or natural extensions that can be motivated the same way — used to defend utilitarianism, i.e. Compensation (and so Impartiality) or Separability.
4. Together, it seems like the major arguments for utilitarianism in the first place actually undermine utilitarianism.

Responses

Things look pretty bad for unbounded utility functions and utilitarianism. However, there are multiple responses someone might give in order to defend them, and I consider three here:

1. We only need to satisfy versions of the principles concerned with prospects with only finitely many outcomes, because infinities are too problematic generally.
2. Accept irrational behaviour (at least in some hypotheticals) or deny its irrationality.
3. Accept violating foundational principles for utilitarianism in the general cases, but this only somewhat undermines utilitarianism, as other theories may do even worse.
4. EDIT to add: The results undermine many other views, not just utilitarianism.

To summarize my opinion on these, I think 1 is a bad argument, but 2, 3 and 4 seem defensible, although 2 and 3 accept that expected utility maximization and utilitarianism are at least somewhat undermined, respectively. On 4, I still think utilitarianism takes the bigger hit, but that doesn't mean it's now less plausible than alternatives. I elaborate below.

Infinities are generally too problematic

First, one might claim the generalizations of axioms of expected utility theory, especially Independence or the Sure-Thing Principle, or even Separability, as well money pumps and Dutch books in general, should count only for prospects over finitely many possible outcomes, given other problems and paradoxes with infinities for decision theory, even expected utility theory with bounded utilities, as discussed in Arntzenius et al., 2004, Peterson, 2016 and Bales, 2021. Expected utility theory with unbounded utilities is consistent with the finitary versions, and some extensions of finitary expected utility theory are also consistent with Stochastic Dominance applied over all prospects, including those with infinitely many possible outcomes (Goodsell, 2023, see also earlier extensions of finitary expected utility to satisfy statewise dominance in Colyvan, 2006, Colyvan, 2008, which can be further extended to satisfy Stochastic Dominance^[24]). Stochastic Dominance, Compensation and the finitary version of Separability are also jointly consistent (Russell, 2023). However, I find this argument unpersuasive:

1. Plausible and rational decision theories can accommodate infinitely many outcomes, e.g. with bounded utility functions. Not all uses of infinities are problematic for decision theory in general, so the argument from other problems with infinities doesn’t tell us much about these problems. Measure theory and probability theory work fine with these kinds of infinities. The argument proves too much.
2. It’s reasonable to consider prospects with infinitely many possible outcomes in practice (e.g. for the “lifetime” of our universe, for sizes of the multiverse, the possibility of continuous spacetime, for the number of moral patients in our multiverse, Russell, 2023), and it’s plausible that all of our prospects have infinitely many possible outcomes, so our decision theory should handle them well. One might claim that we can uniformly bound the number of possible outcomes by a finite number across all prospects. But consider the maximum number across all prospects, and a maximally valuable (or maximally disvaluable) but finite value outcome. We should be able to consider another outcome not among the set. Add a bit more consciousness in a few places, or another universe in the multiverse, or extend the time that can support consciousness a little. So, the space of possibilities is infinite, and it’s reasonable to consider prospects with infinitely many possible outcomes. Furthermore, a probabilistic mixture of any prospect with a heavy-tailed prospect (St Petersburg-like, infinite or undefined expected utility) is heavy-tailed. If you think there's some nonzero chance that it's heavy-tailed, then you should believe now that it's heavy-tailed. If you think there's some nonzero chance that you'd come to believe there's some nonzero chance that it's heavy-tailed, then you should believe now that it's heavy-tailed. You'd need absolute certainty to deny this.
3. It’s plausible that if we have an unbounded utility function (or similarly unbounded preferences), we are epistemically required to treat all of our prospects as involving St Petersburg game-like subdistributions, because we can’t justify ruling them out with certainty (see also Cromwell's rule - Wikipedia). It would be objectionably dogmatic to rule them out.
4. This doesn’t prevent irrational behaviour in theory. If we refuse to rank St Petersburg-like prospects as strictly preferable to each of their outcomes, we give up statewise (and stochastic) dominance or transitivity (see the previous footnote ^[11]), each of which is irrational. If we don’t (e.g. following Goodsell, 2023), the same arguments that support the finite versions of Independence and the Sure-Thing Principle can be made against the countable versions (e.g. Russell and Isaacs, 2021, the money pump argument earlier). And the Egyptology objection for Separability generalizes, too (as pointed out in Russell, 2023). If those arguments don’t have (much) force in the general cases, then they shouldn’t have (much) force in the finitary cases, because the arguments are the same.

Accept irrational behaviour or deny its irrationality

A second response is to just bite the bullet and accept apparently irrational behaviour in some (at least hypothetical) circumstances, or deny that it is in fact irrational at all. However, this, too, weakens the strongest arguments for expected utility maximization. The hypothetical situations where irrational decisions would be forced could be unrealistic or very improbable, and so seemingly irrational behaviour in them doesn’t matter, or matters less. The money pump I considered doesn’t seem very realistic, and it’s hard to imagine very realistic versions. Finding out the actual value (or a finite upper bound on it) of a prospect with infinite expected utility conditional on finite actual utility would realistically require an unbounded amount of time and space to even represent. Furthermore, for utility functions that scale relatively continuously with events over space and time, with unbounded time, many of the events contributing utility will have happened, and events that have already happened can’t be traded away. That being said:

1. The issues with the money pump argument don't apply to the impossibility theorems for Stochastic Dominance, Impartiality (or Compensation) and Anteriority or Separability. Those are arguments about the right kinds of views to hold. The proofs are finite, and at no point do we need to imagine someone or something with arbitrarily large representations of value (except the outcome being a representation of itself).
2. I expect the issue about events already happening to be addressable in principle by just subtracting from B - $100 the value in A already accumulated in the time it took to estimate the actual value of A, assuming this can be done without all of A’s value having already been accumulated.

Still, let's grant that there's something to this, and we don't need to be meet these requirements all of the time or at least in all hypotheticals. Then, other considerations, like Separability, can outweigh them. However, if expectational total utilitarianism is still plausible despite irrational behaviour in unrealistic or very improbable situations, then it seems irrational behaviour in unrealistic or very improbable situations shouldn’t count decisively against other theories or other normative intuitions. So, we open up the possibility to decision theories other than expected utility theory. Furthermore, the line for “unrealistic or very improbable” seems subjective, and if we draw a line to make an exception for utilitarianism, there doesn’t seem to be much reason why we shouldn’t draw more permissive lines to make more exceptions.

Indeed, I don’t think instrumental rationality or avoiding money pumps in all hypothetical cases is normatively required, and I weigh them with my other normative intuitions, e.g. epistemic rationality or justifiability (e.g. Schoenfield, 2012 on imprecise credences). I’d of course prefer to be money pumped or violate Stochastic Dominance less. However, a more general perspective is that foreseeably doing worse by your own lights is regrettable, but regrettable only to the extent of your actual losses from it. There are often more important things to worry about than such losses, like situations of asymmetric information, or just doing better by the lights of your other intuitions. Furthermore, having to abandon another principle or reason you find plausible or otherwise change your views just to be instrumentally rational can be seen as another way of foreseeably doing worse by your own lights. I'd rather hypothetically lose than definitely lose.

Sacrifice or weaken utilitarian principles

A third response is of course to just give up or weaken one or more of the principles used to support utilitarianism. We could approximate expectational total utilitarianism with bounded utility functions or just use stochastic dominance over total utility (Tarsney, 2020), even agreeing in all deterministic finite population cases, and possibly “approximately” satisfying these principles in general. We might claim that moral axiology should only be concerned with betterness per se and deterministic cases. On the other hand, risk and uncertainty are the domains of decision theory, instrumental rationality and practical deliberation, just aimed at ensuring we act consistently with our understanding of betterness. What you have most reason to do is whatever maximizes actual total welfare, regardless of your beliefs about what would achieve this. It’s not a matter of rationality that what you should do shouldn’t depend on things unaffected by your decisions even in uncertain cases or that we should aim to maximize each individual’s expected utility. Nor are these matters of axiology, if axiology is only concerned with deterministic cases. So, Separability and Pareto only need to apply in deterministic cases, and we have results that support total utilitarianism in finite deterministic cases based on them, like Theorem 3 of Blackorby et al., 2002 and section 5 of Thomas, 2022.

That the deterministic and finitary prospect versions of these principles are jointly consistent and support (extensions of) (expectational total) utilitarianism could mean arguments defending these principles provide some support for the view, just less than if the full principles were jointly satisfiable. Other views will tend to violate restricted or weaker versions or do so in worse ways, e.g. not just failing to preserve strict inequalities in Separability but actually reversing them. Beckstead and Thomas, 2023 (footnote 19) point to “the particular dramatic violations [of Separability] to which timidity leads.” If we find the arguments for the principles intuitively compelling, then it’s better, all else equal, for our views to be “more consistent” with them than otherwise, i.e. satisfy weaker or restricted versions, even if not perfectly consistent with the general principles. Other views could still just be worse. Don't let the perfect be the enemy of the good, and don't throw the baby out with the bathwater.

It's not just utilitarianism

EDIT: A final response is to point out that these results undermine much more than just utilitarianism. If we give up Anteriority, then we give up Strong Ex Ante Pareto, and if we give up Strong Ex Ante Pareto, we have much less reason to satisfy its restriction to deterministic cases, Strong Pareto, because similar arguments support both. Strong Pareto seems very basic and obvious: if we can make an individual or multiple individuals better off without making anyone worse off,^[25] we should. Having to give up Impartiality or Anteriority, and therefore it seems, Impartiality or Strong Pareto, puts us in a similar situation as infinite ethics, where extensions of Impartiality and Pareto are incompatible in deterministic cases with infinite populations (Askell, 2018, Askell, Wiblin and Harris, 2018). However, in response, I do think there's at least one independent reason to satisfy Strong Pareto but not (Strong) Ex Ante Pareto or Anteriority: extra concern for those who end up worse off (ex post equity) like an (ex post) prioritarian, egalitarian or sufficientarian. Priority for the worse off doesn't give us a positive argument to have a bounded utility function in particular or avoid the sorts of problems here (even if not exactly the same ones). It just counts against some positive arguments to have an unbounded utility function, specifically the ones depending on Anteriority or Ex Ante Pareto. But that still takes away more from what favoured utilitarianism than from what favoured, say, (ex post) prioritarianism. It doesn't necessarily make prioritarianism or other views more plausible than utilitarianism, but utilitarianism takes the bigger hit to its plausibility, because what seemed to favour utilitarianism so much has turned out to not favour it as much as we thought. You might say utilitarianism had much more to lose, i.e. Harsanyi's theorem and generalizations.

Acknowledgements

Thanks to Jeffrey Sanford Russell for substantial feedback on a late draft, as well as Justis Mills and Hayden Wilkinson for helpful feedback on an earlier draft. All errors are my own.

1. ^{^}

    An individual’s welfare can be the value of their own utility function, although preferences or utility functions defined in terms of each other can lead to contradictions through indirect self-reference (Bergstrom, 1989, Bergstrom, 1999, Vadasz, 2005, Yann, 2005 and Dave and Dodds, 2012). I set aside this issue here.

2. ^{^}

   This argument works with a step size that's bounded below, even by a tiny value, like 1 millionth of a second or 1 millionth more (counterfactual) utility. If the step sizes have to keep getting smaller and smaller and converge to 0, then we may never reach K.

3. ^{^}

   Although there are stronger arguments that's actually infinite. It's one of the simplest and most natural models that fits with our observations of global flatness. See the Wikipedia article Shape of the Universe.

^{^}

 For generalizations without actual utility values, see violations of Limitedness in Russell and Isaacs, 2021 and reckless preferences in Beckstead and Thomas, 2023.

^{^}

Independence: For any prospects X, Y and Z, and probability p,0<p<1, if X<Y, then pX+(1−p)Z<pY+(1−p)Z, 

where pX+(1−p)Z is the prospect that's X with probability p, and Z with probability 1−p.

 

Russell and Isaacs, 2021 define Countable Independence as follows:

For any prospects X1,X2,…, and Y1,Y2,…, and any probabilities p1,p2,… that sum to one, if X1≲Y1,X2≲Y2,…, then

∑ipiXi≲∑ipiYi

If furthermore Xj<Yj for some j such that pj>0, then

∑ipiXi<∑ipiYi

The standard finitary Independence axiom is a special case.

^{^}

The Sure Thing Principle can be defined as follows:

Let A and B be prospects, and let E be some event with probability neither 0 nor 1. If A≲B conditional on each of E and not E, then A≲B. If furthermore, A<B conditional on E or A < B conditional on not E, then A<B.

In other words, if we weakly prefer B either way, then we should just weakly prefer B. And if, furthermore, we strictly prefer B on one of the two possibilities, then we should just strictly prefer B.

 

Russell and Isaacs, 2021 define the Countable Sure Thing Principle as follows:

Let A and B be prospects, and let E be a (countable) set of mutually exclusive and exhaustive events, each with non-zero probability. If A≲B conditional on each E∈E, then A≲B. If furthermore, A<B conditional on some E∈E, then A<B.

^{^}

 See also Christiano, 2022. Both depend on St Petersburg game-like prospects with infinitely many possible outcomes and, when defined, infinite expected utility. For more on the St Petersburg paradox, see Peterson, 2023. Some other foreseeable sure loss arguments require a finite but possibly unbounded number of choices, like McGee, 1999 and Pruss, 2022.

^{^}

 Or, as in Russell and Isaacs, 2021, each of the countably many prospects used to construct it.

^{^}

Note that the probabilities sum to 1, because ∑∞n=11/2n=1, so this is in fact a proper probability distribution.

The expected value is ∑∞n=12n12n=limN→∞∑Nn=11=limN→∞N=∞

^{^}

 From u(xn+1)≥2u(xn) for each n>1, we have, by induction, u(xn+1)≥2nu(xn). Then, for each N≥1,

E[u(X)]=∑∞n=1u(xn)p(xn)=∑∞n=1u(xn)12n≥∑Nn=1u(xn)/2n≥∑Nn=12n−1u(x1)/2n=Nu(x1)/2,

which can be arbitrarily large, so E[u(X)]=∞.

^{^}

This would follow either by extension to expected utilities over countable prospects, or assuming we respect Statewise Dominance and transitivity.

For the latter, we can modify the prospect to a truncated one with finitely many outcomes XN for each N>1, by defining XN=X if X<xN, and XN=xN (or x1) otherwise. Then E[u(XN)] is finite for each N, but limN→∞E[u(XN)]=∞. Furthermore, for each N, not only is it the case that E[u(X)]=∞>E[u(XN)], but X also strictly statewise dominates XN, i.e. X is with certainty at least as good as XN, and is, with nonzero probability, strictly better. So, given any prospect Y with finite (expected) utility, there’s an N such that E[u(XN)]>E[u(Y)], so XN≻Y, but since X≻XN, by transitivity, X≻Y.

^{^}

For Countable Independence: We defined X=∑∞n=112nxn. We can let Xn=xn in the definition of Countable Independence. However, it's also the case that X=∑∞n=112nX, so we can let Yn=X in the definition of Countable Independence. But Yn=X>xn=Xn for each n, so by Countable Independence, X>X, contrary to reflexivity.

 

For the Countable Sure-Thing Principle: define Y to be identically distributed to X but independent from X. Let E={X=xn|n≥1}. Y>xn for each n, so Y>X conditional on X=xn, for each n. By the Countable Sure-Thing Principle, this would imply Y>X. However, doing the same with E={Y=xn|n≥1} also gives us X>Y, violating transitivity.

 

These arguments extend to the more general kinds of improper prospects in Russell and Isaacs, 2021.

^{^}

In practice, you should give weight to the possibility that it has infinite or undefined value. However, the argument that follows can be generalized to this case using stochastic dominance reasoning or, if you do break ties between actual infinities, any reasonable way of doing so.

^{^}

 Or give you an accurate finite upper bound on how it will turn out.

^{^}

And the genie isn’t going to do anything good with it.

^{^}

Interestingly, if expectational total utilitarianism is consistent with Harsanyi’s theorem, then it is not the only way for total utilitarianism to be consistent with Harsanyith’s theorem. Say individual welfare takes values in the interval [2,3]. Then the utility functions ∑Nn=1ui+N and N∑Nn=1ui agree with both Harsanyi’s theorem and total utilitarianism. According to them, a larger population is always better than a smaller population, regardless of the welfare levels in each. However, some further modest assumptions give us expectational total utilitarianism, e.g. each individual can welfare level 0.

^{^}

So, assuming reflexivity, transitivity, the Independence of Irrelevant Alternatives. Also, we need the set of prospects to be rich enough to include some of the kinds of prospects used in the proofs.

^{^}

Exceptions include average utilitarianism, symmetric person-affecting views, maximin and maximax.

^{^}

Russell, 2023 writes:

Stochastic Dominance is a fairly uncontroversial principle of decision theory—even among those who reject other parts of standard expectational decision theory (such as Quiggin, 1993; Broome, 2004), and even in settings where other parts of standard expectational decision theory give out (see for example Easwaran, 2014).¹⁰ We should not utterly foreclose giving up Stochastic Dominance—we are facing paradoxes, so some plausible principles will have to go—but I do not think this is a very promising direction. In what follows, I will take Stochastic Dominance for granted.

and in footnote 10:

For other defenses of Stochastic Dominance, on which I here have drawn, see Tarsney (2020, 8); Wilkinson (2022, 10); Bader (2018).

^{^}

There is some controversy here, because we might instead say that A statewise dominates B if and only if A is at least as good as B under every possibility, including each possibility with probability 0. Russell, 2023 writes:

For example, the probability of an ideally sharp dart hitting a particular point may be zero—but the prospect of sparing a child from malaria if the dart hits that point (and otherwise nothing) may still be better than the prospect of getting nothing no matter what. But these two prospects are stochastically equivalent. Perhaps what is best depends on what features of its outcomes are sure—where in general this can come apart from what is almost sure—that is, has probability one.

However, I don’t think this undermines the results of Russell, 2023, because the prospects considered don’t disagree on any outcomes of probability 0.

^{^}

Insofar as it isn’t evidence for how well off moral patients today and in the future can or will be, and ignoring acausal influence.

^{^}

The same objection is raised earlier in McMahan, 1981, p. 115 referring to past generations more generally. See also discussion of it and similar objections in Huemer, 2008, Wilkinson, 2022, Beckstead and Thomas, 2023, Wilkinson, 2023 and Russell, 2023.

^{^}

And a single preorder over prospects, so transitivity, reflexivity and the independence of irrelevant alternatives, and a rich enough set of possible prospects.

^{^}

These can be extended to satisfy Stochastic Dominance by making stochastically equivalent prospects equivalent and taking the transitive closure to get a new preorder.

^{^}

Or, while keeping everyone at least as well off, in cases of incomparability.

Show all footnotes