BLUF: One common supposition is a rational forecast, because it ‘prices in’ anticipated evidence, should follow a (symmetric) random walk. Thus one should not expect a predictable trend in rational forecasts (e.g. 10% day 1, 9% day 2, 8% day 3, etc.), nor commonly see this pattern when reviewing good forecasting platforms. Yet one does, and this is because the supposition is wrong: ‘pricing in’ and reflective equilibrium constraints only entail the present credence is the expected value of a future credence. Skew in the anticipated distribution can give rise to the commonly observed “steady pattern of updates in one direction”. Such skew is very common: it is typical in 'will event happen by date' questions, and one’s current belief often implies skew in the expected distribution of future credences. Thus predictable directions in updating are unreliable indicators of irrationality.
Introduction
Forecasting is common (although it should be commoner) and forecasts (whether our own or others) change with further reflection or new evidence. There are standard metrics to assess how good someone’s forecasting is, like accuracy and calibration. Another putative metric is something like ‘crowd anticipation’: if I predict P(X) = 0.8 when the consensus is P(X) = 0.6, but over time this consensus moves to P(X) = 0.8, regardless of how the question resolves, I might take this to be evidence I was ‘ahead of the curve’ in assessing the right probability which should have been believed given the evidence available.
This leads to scepticism about the rationality of predictors which show a pattern of ‘steadily moving in one direction’ for a given question: e.g. P(X) = 0.6, then 0.63, 0.69, 0.72 … and then the question resolves affirmatively. Surely a more rational predictor, observing this pattern, would try and make forecasts an observer couldn’t reliably guess to be higher or lower in the future, so forecast values follow something like a (symmetrical) random walk. Yet forecast aggregates (and individual forecasters) commonly show these directional patterns if tracking a given question.
Scott Alexander noted curiosity about this behaviour; Eliezer Yudkowsky has confidently asserted it is an indicator of sub-par Bayesian updating.[1] Yet the forecasters regularly (and predictably) notching questions up or down as time passes are being rational. Alexander’s curiosity was satisfied by various comments on his piece, but I write here as this understanding may be tacit knowledge to regular forecasters, yet valuable to explain to a wider audience.
Reflective equilibrium, expected value, and skew
One of the typical arguments against steadily directional patterns is they suggest a violation of reflective equilibrium. In the same way if I say P(X) = 0.8, I should not expect to believe P(X) = 1 (i.e. it happened) more than 80% of the time, I shouldn’t expect to believe P(X) [later] > P(X) [now] more likely than not. If I did, surely I should start ‘pricing that in’ and updating my current forecast upwards. Market analogies are commonly appealed to in making this point: if we know the stock price of a company is more likely than not to go up, why haven’t we bid up the price already?
This motivation is mistaken. Reflective equilibrium only demands one’s current forecast is the expected value of one’s future credence. So although the mean of P(X) [later] should equal P(X) [now], there are no other constraints on the distribution. If it is skewed, then you can have predictable update direction without irrationality: e.g. from P(X) = 0.8, I may think in a week I will - most of the time - have notched this forecast slightly upwards, but less of the time notching it further downwards, and this averages out to E[P(X) [next week]] = 0.8.
One common scenario for this sort of skew to emerge are ‘constant hazard’ forecast questions of the form “Will this event [which could happen ‘at any time’, e.g. a head of state dying, a conflict breaking out] occur before this date?”. As time passes, the window of opportunity for the question resolving positively closes: ‘tomorrow’s prediction’ is very likely to be slightly lower than todays, but with a small chance of being much higher.[2] Thus the common observation of forecasters tracking a question to be notching their forecasts down periodically ‘for the passage of time’. Forecasters trying to ‘price this in early’ by going to 0 or 1 will find they are overconfident rather than more accurate (more later).
Current forecasts generally imply skew (and predictable direction) for future forecasts
Although these sorts of questions are common on forecasting platforms, the predictable directionality they result in might be dismissed as a quirk of question structure: they have a set deadline, and thus the passage of time itself is providing information - you wouldn’t get this mechanistic effect if the question was “what date will X happen?” rather than “will X happen by [date]?”.
But in fact skew is much more general: ‘directionally predictable patterns’ are expected behaviour when a) future forecasts are expected to have better resolution than current forecasts (e.g. because you will have more information, or will have thought about it more), and b) your current prediction is not one of equipoise (e.g. not 50/50 for a binary event which happens or not). In a soundbyte: your current credence governs the bias in its expected future updates.
Suppose I was trying to predict who would win the French presidential election in January 2022 (cf.), and (like the Metaculus aggregate at the time) I thought Macron is a 60% favourite to be reelected. There’s no pure ‘passage of time’ effects on election results, but I would expect my future predictions to be more accurate than my current one: opinion polls a week before the election are better correlated to results than those 5 months before, economic conditions would be clearer, whether any crises or scandals emerge etc. Even without more data, if I plan to spend a lot more time forecasting this question, I might expect my forecasts to improve with more careful contemplation.
As I have Macron as the favourite, this is (hopefully) based on the balance of considerations I have encountered so far tending to favour his re-election versus not. All else equal,[3] this implies a prediction that the next consideration I encounter is more likely to favour Macron than not too: I think I’m more likely to be in a world where Macron is re-elected in the future, and if so I expect the pre-election signs to generally point to this future too.
If the next consideration I come across indeed favours Macron like I expected, I should update a bit more upwards on his reelection chances (say 60% to 63%). This is not a failure of reflective equilibrium: although I should have priced in the expectation for favourable evidence, I only priced in this was what I was likely to see, so confirmation I actually saw it gives further confidence in my mainline Macron-reelected model.[4] If this consideration went the other way, my greater surprise would have pushed me more in the opposite direction (e.g. 60% to 54%, cf.). If this pattern continues, I should be progressively more confident that Macron will be re-elected, and progressively more confident future evidence will provide further support for the same. So, taking an epistemic diary of my earlier predictions, these would often show a pattern of ‘steady updates in one direction’.
The same point can be made graphically. Let the Y axis be credence, and the X axis to be ‘degree of omniscience’. If you’re at 60% given your current state of knowledge, you would expect to end up at 1 more often than 0 if you were to become omniscient. As there’s a 60:40 directional bias for the ‘random walk’ of a single step from here to omniscience, there’s also a similar expected bias for a smaller step from ‘here to a little more omniscient’, or for the net result of multitude of smaller sequential steps: you are expecting to ultimately resolve to 1 or 0, but to 1 more often than 0, so in aggregate the path is biased upwards from the present estimate. Again reflective equilibrium is maintained by the skew of the distribution, which gets steadily more extreme the closer you are to 0 or 1 already. The typical path when gaining understanding is more resilient confidence, and so major jolts in the opposite direction are more and more surprising.
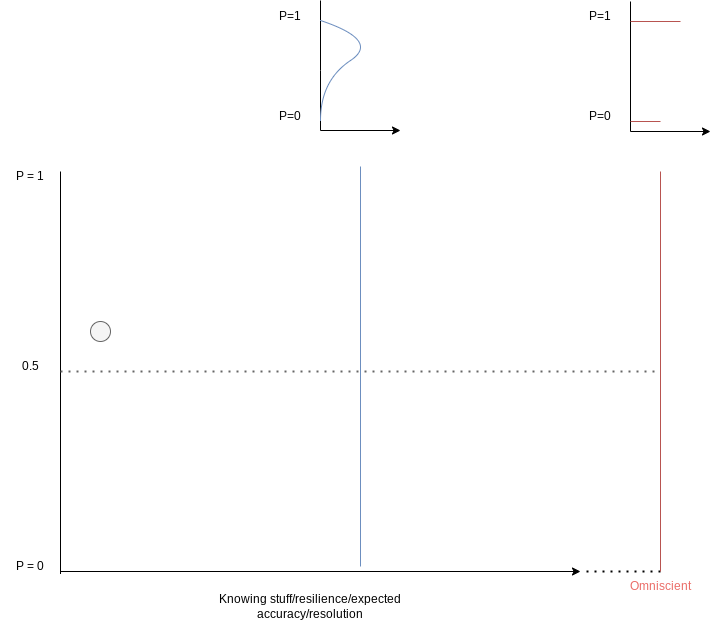
Now consider "Where would you expect your credence to end up if you knew some more (but not everything) about this something? Your credence could walk all over the place across 'epistemic time', but as at the limit you are at the pmf for omniscience, these paths are more likely to be tending towards P=1 than P=0, thus higher than your current estimate. Thus the intermediate pdf forms some skewed distribution with a mean of 0.6, but a mode and median somewhat higher (blue, upper middle panel).
What about forecasting quantities?
For quantitative instead of binary predictions (e.g. ‘how much X?’ or ‘what year X?’), skew is not guaranteed by an initial estimate, but remains common nonetheless. Many quantities of interest are not distributed symmetrically (e.g. exponential for time-to-event, lognormal for conjunctive multipliers, power-law for more network-y generators), kind-of owed to the fact there are hard minimums (e.g. “X happened two years ago” is a very remote resolution to most “when will X happen?” questions; a stock price can’t really go negative).[5]
This skew again introduces asymmetry in update direction: ignoring edge cases like multi-modality, I expect to find myself closer to the modal scenario, so anticipate most of the time the average for my new distribution to track towards the mode of my previous one, but with a smaller chance of new evidence throwing me out along the long tail. E.g. my forecast for a market cap of an early stage start-up is probably log-normalish, and the average likely to go down than up, as I anticipate it to steadily fall in the modal case evidence mounts it is following the modal trajectory (i.e. to the modal outcome of zero), but more rarely it becomes successful and my expected value shoots upwards much higher.
Conclusion
‘Slowly(?) updating in one direction’ can be due to underconfidence or sluggishness. Yet, as demonstrated above, this appearance can also emerge from appropriate and well calibrated forecasts and updating. Assessing calibration can rule in or out predictor underconfidence: 80% events should occur roughly 80% of the time, regardless of whether 80% was my initial forecast or my heavily updated one. Sluggish updating can also be suggested by a trend towards greater underconfidence with prediction number: i.e. in aggregate, my 2nd to nth predictions on a question get steadily more underconfident whilst my initial ones are well-calibrated (even if less accurate). Both require a significant track record (across multiple questions) to determine. But I’d guess on priors less able forecasters tend to err in the opposite directions: being overconfident, and over-updating on recent information.
In contrast, rational predictions which do follow a symmetric random walk over time are constrained to particular circumstances: where you're basically at equipoise, where you're forecasting a quantity which is basically normally distributed, etc. These are fairly uncommon on prediction platforms, thus monotonic traces and skewed forecast distributions are the commoner observations.
Aside: ‘anticipating consensus’ poorly distinguishes overconfidence from edge
As ‘steady updates in one direction’ is a very unreliable indicator of irrationality, so too ‘observing the crowd steadily move towards your position’ is a very unreliable indicator that you are a superior forecaster. Without proper scoring, inferior (overconfident) predictors look similar to superior (accurate) ones.
Suppose one is predicting 10 questions where the accurate and well-calibrated consensus is at 90% for all of them. You’re not more accurate, but you are overconfident, so you extremise to 99% for all of them. Consistent with the consensus estimate, 9/10 happen but 1 doesn’t. In terms of resolution, you see 9 times out of 10 you were on the ‘better side of maybe’ versus the crowd; if there was intermediate evidence being tracked (so 9 of them steadily moved to 1, whilst 1 bucked the trend and went to 0), you’d also see 9 times out of 10 you were anticipating the consensus, which moved in your direction.
Qualitatively, you look pretty impressive, especially if only a few items have resolved, and all in your favour (“This is the third time you thought I was being too confident about something, only for us to find my belief was closer to the truth than yours. How many more times does this have to happen before you recognise you’d be less wrong if you agreed with me?”) Yet in fact you are just a worse forecaster by the lights of any proper scoring rule:[6] the pennies you won going out on a limb nine times does not compensate you for the one time you got steamrollered.
- ^
From a (public) facebook post (so I take the etiquette to be 'fair game to quote, but not to make a huge deal out of'):
To be a slightly better Bayesian is to spend your entire life watching others slowly update in excruciatingly predictable directions that you jumped ahead of 6 years earlier so that your remaining life could be a random epistemic walk like a sane person with self-respect.
I wonder if a Metaculus forecast of "what this forecast will look like in 3 more years" would be saner. Is Metaculus reflective, does it know what it's doing wrong?
- ^
The relevant financial analogy here would be options, which typically exhibit 'time decay'
- ^
Obviously, you might have a richer model where although the totality of evidence favours Macron’s re-election, some families of considerations are adverse. Maybe I think he is going to win despite domestic economic headwinds (which I take to harm his chances). So P(next consideration favours Macron) can be >0.5, yet P(next consideration favours Macron|it's about domestic economics) <0.5.
- ^
So, strictly speaking, you should still be updating off evidence you were expecting to see, so long as you weren't certain it would turn out like you anticipated.
- ^
This is not a foolproof diagnostic. Although it is impossible for a woman to have negative height, and ‘possible’ for her to be 10 ft tall, human height distributions by sex are basically normal distributions, not skewed ones.
- ^
E.g. 0.196 versus 0.180 for your brier score versus the consensus in this toy example (lower is better). The distance between you will vary depending on the scoring rule, but propriety ensures all will rank you worse.

Previously: Mistakes with Conservation of Expected Evidence
What's BLUF?
Bottom line up front
Yeah, I had to look this up
I wish you had said this in the BLUF -- it is the key insight, and the one that made me go from "Greg sounds totally wrong" to "Ohhh, he is totally right"
ETA: you did actually say this, but you said it in less simple language, which is why I missed it
I’m not sure but my guess of the argument of the OP is that:
Let’s say you are an unbiased forecaster. You get information as time passes. When you start with a 60% prediction that event X will happen, on average, the evidence you will receive will cause you to correctly revise your prediction towards 100%.
<Eyes emoji>
The section on forecasting quantities is really a special case of estimating any unknown quantity X given a prior and data when X has a true (but unknown) value different from the prior. You should expect your updates to be roughly monotonic from your prior value to the true value as data accumulates.
For example, if X is vaccine effectiveness of an unusually effective vaccine then the expected value of your prior for X is going to be too small. As studies accumulate, they should all point to the true value of X (up to errors/biases/etc) and your posterior mean should also move towards the true value.
An important difference here is foresight vs hindsight. At any particular time, you expect your future posterior mean of X to be your current posterior mean of X. However, once you know what your final posterior mean of X to be (approximately the true value) then updates up to that point look .
Appendix: maths proving the above for a simple case.
You might be interested in my empirical look at this for Metaculus
Yes, this is completely correct and many people do not get the mathematics right.
One example to think of is “the odds the Earth gets hit by a huge asteroid in the date range 2000-3000”. Whatever the odds are, they will probably steadily, predictably update downwards as time passes. Every day that goes by, you learn a huge asteroid did not hit the earth that day.
Of course, it’s possible an asteroid does hit the Earth and you have to drastically update upwards! But the vast majority of the time, the update direction will be downwards.
I'm confused about your interpretation of Eliezer's words. What he seems to be saying is that recent advances in ML shouldn't have caused such a notable update in predictions on AI timelines on Metaculus, since a more rational predictor would have expected that such things would be happening more likely in this timeframe than the Metaculus crowd apparently did. Admittedly, he may be wrong about that, but I see what he wrote as a claim concerning one particular subject, not about steady updates in one direction in general.
The two quotes seem to be explicitly, specifically about the general process of “updating” (although with some stretching, the first quote below could also be rationalized by saying the forecasters are obtuse and incredibly bad—but if you think people are allowed to have different beliefs, then the trend indicated should occur).
My current model is that seeing predictable updating is still bayesian evidence of people following subpar algorithm, though it's definitely not definite evidence.
To formalize this, assume you have two hypotheses about how Metaculus users operate:
H1: They perform correct bayesian updates
H2: They update sluggishly to new evidence
First, let's discuss priors between these two hypotheses. IIRC we have a decent amount of evidence that sluggish updating is a pretty common occurrence in forecasting contexts, so raising sluggish updating in this context doesn't seem unreasonable to me. Also, anecdotally, I find it hard to avoid sluggish updating, even if I try to pay attention to it, and would expect that it's a common epistemic mistake.
Now, predictable updating is clearly more likely under H2 than under H1. The exact odds ratio of course depends on the questions being asked, but my guess is that in the context of Metaculus, something in the range of 2:1 for the data observed seems kind of reasonable to me (though this is really fully made up). This means the sentence that if you don't have the problem of sluggish updating, you frequently see people update slowly in your direction, seems correct and accurate.
I do think Eliezer is just wrong when he says that a proper bayesian would have beliefs that look like a "random epistemic walk", unless that "epistemic" modifier there is really doing a lot of work that is not-intuitive. If I am not super confused, the only property that sequences of beliefs should fulfill based on conservation of expected evidence is the Martingale property, which is a much broader class than random walks.
Thank you for this thoughtful reply.
I don’t have any knowledge that would add to this discussion.
With that personal limitation in mind, what you said you seems very informative and useful, including the composition of what fraction of people are poorly updating. The experience you express here about forecasting and other belief updating seems enormous.