TLDR: Our method can be used to forecast the cost-effectiveness of potential future R&D projects. Its predictions for a completed behavioral science R&D project were surprisingly accurate.
Relative to R&D’s high social return on investment (Jones & Summers, 2021; Pardey et al., 2016; Kremer et al., 2019; Broussard et al., 2022), the EA community invests a surprisingly small proportion of its funds into EA-aligned R&D projects (Lieder & McGuire, 2022). One contributing factor could be that it is extremely difficult to predict which of a thousand potential R&D projects would be highly successful. A priori, we don't know whether an R&D project will produce an intervention that is much more cost-effective than any currently existing interventions, an intervention that will never be used in practice, or something in-between. We could do much more good with our limited resources if we could predict which R&D projects will succeed in inventing highly cost-effective innovations for generating social value.
Although we cannot predict the future with certainty, we can calculate the expected social return on investment for funding an R&D project given the information available before the project is conducted. Better methods for making such predictions with confidence could make it easier for funders and policymakers to endorse groundbreaking, innovative projects with a high expected positive impact. This would be an important corrective for the funding agencies’ tendency to reject proposals that don’t already have a compelling track record in favor of projects that are less novel and less innovative but more likely to succeed (Boudreau et al., 2016; Good Science Project, 2023).
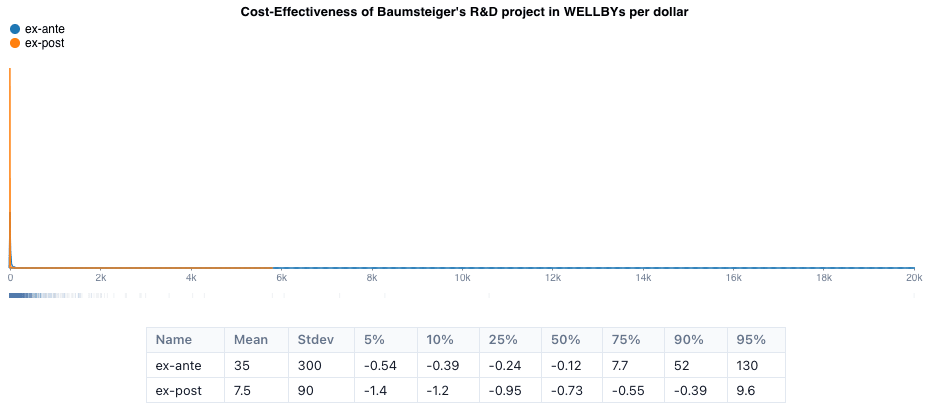
This post describes a systematic method for calculating probabilistic forecasts about the cost-effectiveness of potential R&D before they are funded. We provide a proof-of-concept for the feasibility of this approach by applying it to predict the cost-effectiveness of a behavioral science R&D project. Our method predicted funding the project would be more than 100x as cost-effective as donating to the best charities working on global health and well-being, and our ex-post impact assessment confirmed that prediction. Concretely, our method’s prediction of 35 WELLBYs per dollar – which was based exclusively on information that was available before the project was conducted –deviated from the ex-post assessment of the project’s outputs (i.e., 7.5 WELLBYs per dollar) by less than one order of magnitude.
Method for predicting the ex-ante cost-effectiveness of R&D projects
We define the ex-ante cost-effectiveness of an R&D project as the expected value of its ex-post cost-effectiveness, given only the information that is available before the project is conducted. This expected value corresponds to the weighted average of the project's ex-post cost-effectiveness across all possible values of the effectiveness of the new intervention (), the scalability of the new intervention (), and the cost of the R&D project (). In this weighted average, the weight of each possible combination of values is its ex-ante probability.
To compute the predicted ex-ante cost-effectiveness defined in the above equation, we adapt the ex-post method described in the previous post such that the posterior distributions of the project’s cost and the intervention’s cost-effectiveness and scalability are replaced by the corresponding prior distributions that encode only the information that was available before the project was initiated. As summarized in Table 2, this modified method proceeds in three steps. The first and most difficult step is to forecast the expected increase in moral value that the R&D project would generate if it were conducted. The second step is predicting how much the R&D process would cost. The third step is to combine the probabilistic predictions of Steps 1 and 2 into a prediction of the project’s cost-effectiveness ratio.
Table 2. Procedure for predicting the ex-ante cost-effectiveness of a potential future R&D project.
| Step | |
1 | Predict the cost-effectiveness of the new intervention(s) the project might produce:
|
2 | Predict the moral value that would be created using the new intervention:
|
3 | Predict the project’s costs and cost-effectiveness:
|
Step 1: Predict the cost-effectiveness of the new intervention(s) the project might produce.
To predict the cost-effectiveness of a potential new intervention before it has been developed, we extrapolate from historical data on the successes and failures of previous R&D projects. To obtain a conservative estimate, we assume that there were no systematic improvements in the effectiveness of new interventions over time. Under this assumption, we can approximate the probability distribution of the effectiveness of new interventions by reference class forecasting (Flyvbjerg, 2006). Reference class forecasting uses quantitative data from similar projects to curb optimistic biases in people's intuitive predictions (Kahneman & Tversky, 1979). The idea is to predict attributes of future projects, such as how long it will take to complete them, from objective data about similar projects that have been conducted in the past (i.e., the project's reference class). We develop new probabilistic reference-class forecasting methods for predicting the outcomes and impact of R&D projects. The details of these methods are described in Section 3.2 of the Observable Notebook accompanying this post.
Our method can be applied even when the effectiveness of previous interventions was assessed in terms of outcomes other than the benefit of interest (e.g., behavior change rather than well-being). In those cases, our method develops an evidence-based probabilistic causal model linking the outcome variables of those studies to the benefit of interest (see Post 2 for an illustration of how this can be done).
Step 1b predicts the cost of deploying the intervention per person who completes it. This includes the cost of directing people to the intervention (e.g., online advertising) and the cost of conducting it. Finally, Step 1c combines the predictions of Step 1a and Step 1b into a prediction of the cost-effectiveness of the potential future intervention.
Step 2: Predict the moral value that would be created using the new intervention
The second step of our ex-ante method is identical to the second step in our ex-post method (see Section 2 of Post 4) because both involve predicting the benefits of future applications.
Step 3: Combine the estimates of expected costs and benefits
To predict a project’s cost (Step 3a), our method first identifies a reference class of similar completed projects or funded grant proposals. The actual or projected costs of those projects are then used to predict the cost of the proposed R&D project. Concretely, you can use the histogram of the previous projects’ costs as an empirical estimate of the probability distribution of the cost of the new project. Finally, Step 3b predicts the project’s cost-effectiveness by combining the probability distributions calculated in Steps 2c and 3a.
Proof of concept: Predicting the ex-ante cost-effectiveness of Baumsteiger’s R&D project
To illustrate how our method can be applied to real R&D projects and demonstrate that it works, we applied it to the running example of this sequence: Baumsteiger’s online intervention for promoting prosocial behavior (Baumsteiger, 2019). In the previous post, we evaluated the project’s ex-post cost-effectiveness based on its outputs. By contrast, in this post, we predict the project’s ex-ante cost-effectiveness using only the information that was available before the project was conducted. We then evaluate this prediction against how the project turned out according to the ex-post analysis reported in the previous post.
As in the previous posts, we provide only a brief summary of the analyses. If you want to see the details of how we applied our method to Baumsteiger’s R&D project, you are welcome to peruse Section 3.2 of the project’s Observable notebook.
Step 1: How cost-effective should we have expected Baumsteiger’s intervention to turn out a priori?
The goal of Baumsteiger’s R&D project was to develop a digital psychological intervention for promoting prosocial behavior. So, in this case, the effectiveness of the intervention is the size of its effect on the frequency of prosocial behavior. We, therefore, derive our probabilistic prediction of its effectiveness from the effect sizes of previous psychological interventions for promoting prosocial behavior. Because Baumsteiger’s study was published in July 2019, we only consider studies published before 201
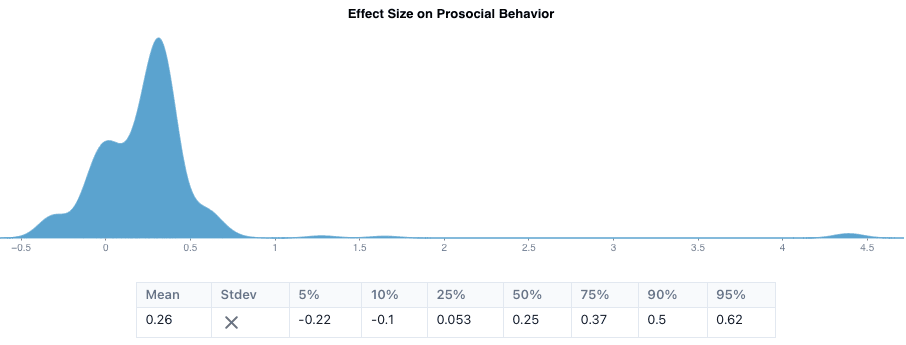
To identify such studies, we draw on three meta-analyses (Mesurado et al., 2019; Menting et al., 2013; Shin & Lee, 2021) and a systematic review (Laguna et al., 2020). Our systematic meta-analysis identified a total of 30 relevant intervention-outcome pairs. Applying our reference class forecasting methods to this data produced the following probabilistic forecast of the new intervention’s effectiveness at promoting prosocial behavior:
The plot above shows that, in expectation, we predict that a new intervention would increase the number of prosocial behaviors a person engages in by about 0.26 standard deviations immediately after the person completes the intervention. This is a small effect. However, as the plot above shows, the data suggests that medium-sized and large effects are also possible (95% C.I. [-0.22, 0.62]).
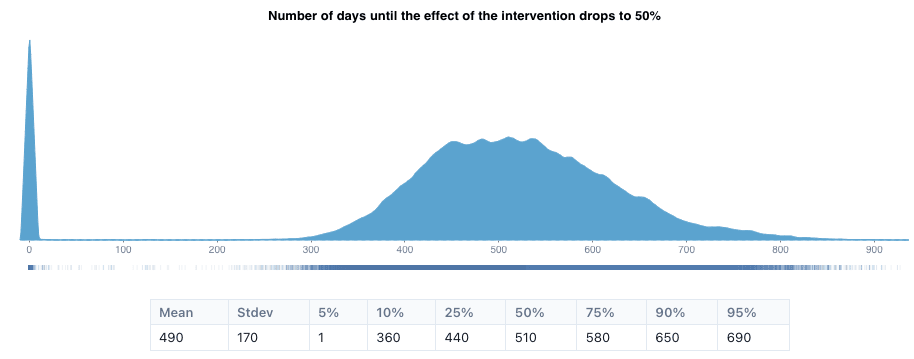
To predict the total benefit of the intervention, we also have to predict how long the benefits will last, in terms of how quickly they decrease over time. To estimate this, we performed Bayesian inference on the half-life of the effects of interventions for promoting prosocial behavior. To achieve this, we applied the method we recently developed for this purpose (Lieder, 2022) to the data from previous experiments on promoting prosocial behavior. We included all such studies that were listed in the systematic review and pertinent meta-analyses listed above (Laguna et al., 2020; Mesurado et al., 2019; Shin & Lee, 2021) that met our inclusion criteria and included at least one follow-up assessment. As shown below, our method inferred that the effects of prosocial behavior interventions either don’t last or, which is more likely, last for at least a couple of years. On average, it appears to take about 500 days until the initial effect decays to about 50% of its original size.
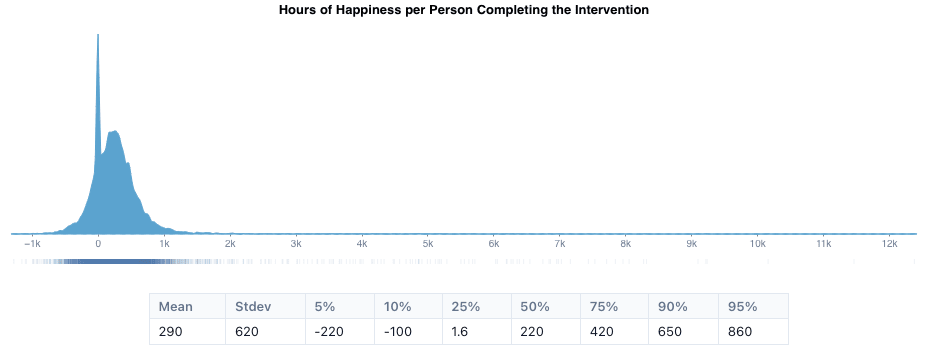
We then combined our prediction of a new intervention’s effect on well-being with the estimate of the cost of deploying online interventions from our library of reusable cost-effectiveness analysis functions. As shown in the figure below, this analysis predicted that the expected ex-ante cost-effectiveness of a new intervention for promoting prosocial behavior is about 140 hours of happiness per dollar (90% C.I. [-88, 550]).
Step 2: Predicting the moral value that could be created with a new intervention for promoting prosocial behavior
We predicted the potential new intervention’s scalability (Step 2a) using the same approach we used for Baumsteiger’s existing intervention. We again found that the uncertainty and potential of the new intervention would warrant evaluating it in an RCT (Step 2b). Next, in Step 2c we found that, in expectation, developing a new intervention for promoting prosocial behavior would increase the amount of well-being that society will create in the future by about 270 million hours of happiness. That is about 8 million well-being-adjusted life years (95% C.I. [-120K; 32M]).
Step 3: Predicting the ex-ante cost-effectiveness of developing a new online intervention for promoting prosocial behavior
To predict the cost of developing a new intervention for promoting prosocial behavior (Step 3a), we first identified a reference group of projects that developed similar interventions for positive character development. I identified those projects by screening all grants that the Templeton World Charity Foundation in the funding area “Character and Virtue Development” as part of their priority “Global Innovations for Character and Virtue Development”. The screening criterion was that the project developed a new psychological intervention. I then compiled a list of the size of those grants. I then used the histogram of those amounts as an empirical estimate of the cost of developing a new intervention for promoting prosocial behavior. According to this method, the expected cost of developing such an intervention is $340,000 (95% C.I. [$220k, $1M]).
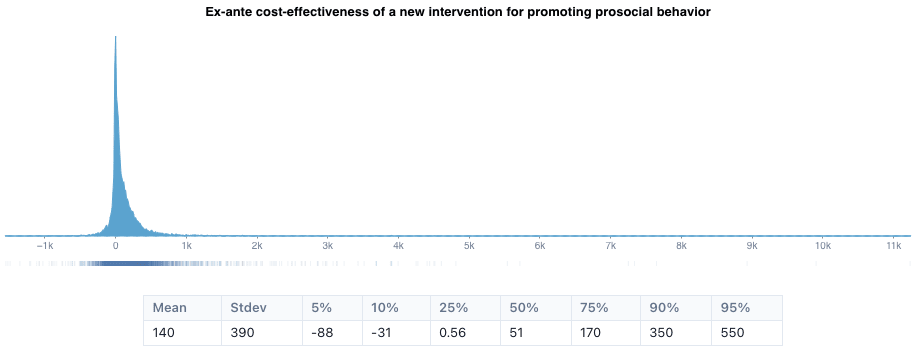
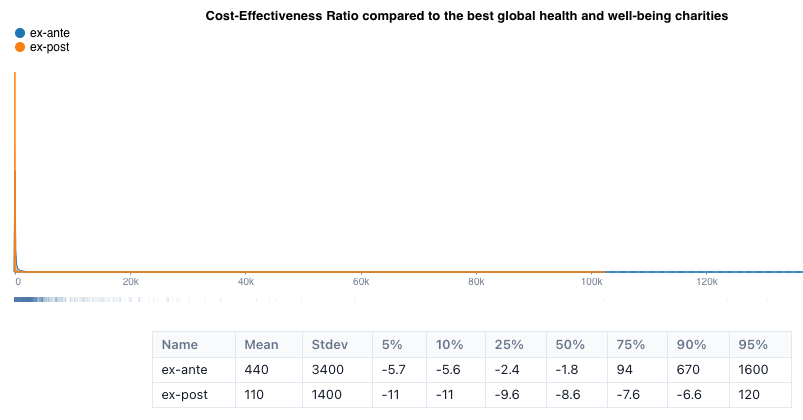
Combining the predicted cost of developing the intervention with its predicted benefits (Step 3b) led to the prediction that the expected cost-effectiveness of developing a new intervention for promoting prosocial behavior was about 35 well-being-adjusted life years per dollar. As shown below, this predicted cost-effectiveness of such projects has a long right tail. This means that while there is a high probability that such projects will be unsuccessful, there is a chance that such a project can be extremely cost-effective. Concretely, our method predicts that there is a 25% chance that developing a new intervention for promoting prosocial behavior would be more than 10x as effective as the best charities in global health and well-being. However, there is also a more than 50% chance that the project would fail to produce moral value.
How accurate was this prediction?
We found that our ex-ante method’s prediction of 35 WELLBYs per dollar – which was based exclusively on information that was available before the project was conducted – was extremely close to the ex-post assessment of the project’s outputs, that is 7.5 WELLBYs per dollar. This is remarkable because the two estimates were derived from different data sources under high levels of uncertainty.
What matters most about the accuracy of our method is not the absolute value of its predictions, but the quality of the decisions it recommends. Those decisions depend primarily on how the cost-effectiveness of the R&D project compares to the cost-effectiveness of the best alternatives. Therefore, a more practically relevant metric is whether our method correctly predicts whether funding a specific R&D project will be more cost-effective than donating to highly effective charities. On that metric, we find that our method predicted that funding Baumsteiger's R&D project could have been more than 100x as cost-effective as the best charities for promoting global health and well-being. Critically, according to our ex-post cost-effectiveness analysis, the project's outcomes confirmed this prediction.
Discussion
We have introduced a method for predicting the cost-effectiveness of an R&D project before it is undertaken. It can therefore be used to decide whether a proposed R&D project is worth funding. We then reported a proof-of-concept illustration showing that this method can be used to predict the cost-effectiveness of developing a psychological intervention for promoting altruism.
Our method correctly predicted that the behavioral science R&D project by Baumsteiger (2019) was highly cost-effective. The accuracy of our method’s prediction was extremely encouraging. However, so far, this method can only be applied to a single R&D project. Therefore, future work should evaluate its accuracy on at least 10 additional R&D projects. If these additional evaluations confirm the apparent accuracy of our ex-ante method, this would suggest that it can be used to support funding decisions for R&D projects. In the future, this could make it easier for funders and policymakers to endorse groundbreaking, innovative projects with a high expected positive impact. This could potentially help mitigate funding agencies’ tendency to reject proposals that don’t already have a compelling track record in favor of projects that are less novel and less innovative but more likely to succeed (Boudreau et al., 2016; Good Science Project, 2023). Perhaps, better methods for predicting the cost-effectiveness of R&D projects could also help reduce the discrepancy between the high-cost-effectiveness of R&D at creating social value (Jones & Summers, 2021) and the surprisingly low proportion of EA funds allocated to scientific research, innovation, and the development of new interventions (Lieder & McGuire, 2022).
Our ex-ante method also allows the cost-effectiveness of R&D to be compared with the cost-effectiveness of donating to charities doing direct work on global health and well-being. Here, we found that our ex-ante method confirmed the ex-post method’s assessment that the development of Baumsteiger’s psychological intervention for promoting prosocial behavior was more cost-effective than promoting health and well-being directly. This suggests that R&D projects aiming to produce psychological interventions for promoting altruism can be much more cost-effective than promoting health and well-being directly.
References
- Baumsteiger, R. (2019). What the world needs now: An intervention for promoting prosocial behavior. Basic and applied social psychology, 41(4), 215-229.
- Boudreau, K. J., Guinan, E. C., Lakhani, K. R., & Riedl, C. (2016). Looking across and looking beyond the knowledge frontier: Intellectual distance, novelty, and resource allocation in science. Management science, 62(10), 2765-2783.
- Broussard, N. H., Chomitz, K. M., Chowdhuri, R. N., Sturla, K., Ssentongo, J., & Zwane, A. P. (2022). Assessing the Social Returns to Innovation for Development: The Global Innovation Fund’s Impact to Date. Working Paper. https://www.globalinnovation.fund/wp-content/uploads/2022/03/GIF-SROI-March-2022-Draft.pdf
- Caprara, G. V., Kanacri, B. P. L., Gerbino, M., Zuffiano, A., Alessandri, G., Vecchio, G., ... & Bridglall, B. (2014). Positive effects of promoting prosocial behavior in early adolescence: Evidence from a school-based intervention. International Journal of Behavioral Development, 38(4), 386-396.
- Flyvbjerg, B. (2008). Curbing optimism bias and strategic misrepresentation in planning: Reference class forecasting in practice. European planning studies, 16(1), 3-21.
- Good Science Project (2023). Why science funders should try to learn from past experience. https://goodscienceproject.org/articles/why-science-funders-should-try-to-learn-from-past-experience/
- Jones, B. F., & Summers, L. H. (2021). A calculation of the social returns to innovation. In Goolsbee and Jones (Eds). Innovation and Public Policy, pp. 15-39. National Bureau of Economic Research. DOI: 10.3386/w27863.
- Kahneman, D., & Tversky, A. (1979). Intuitive prediction: Biases and corrective procedures. In S. Makridakis & S. C. Wheelwright (Eds.). Studies in the Management Sciences: Forecasting, p.12 (Amsterdam: North Holland).
- Kremer, M., Gallant, S., Rostapshova, O., Thomas, M., Chomit, K., Carbonell, J., ... & Jaffe, A. (2019). Is development innovation a good investment? Which innovations scale? Evidence on social investing from USAID’s Development Innovation Ventures. Working paper.
- Laguna, M., Mazur, Z., Kędra, M., & Ostrowski, K. (2020). Interventions stimulating prosocial helping behavior: A systematic review. Journal of Applied Social Psychology, 50(11), 676-696.
- Lieder, F. (2022). Predicting how the effect of a psychological intervention would change over time. https://docs.google.com/document/d/1hU7TyBB0XEWaa-ZMCJwJzjRF5AH4XTXyaRPo5rr-iM0/edit?usp=sharing
- Lieder, F., & McGuire, J. (2022). Finding before funding: Why EA should probably invest more in research. Effective Altruism Forum, https://forum.effectivealtruism.org/posts/FqLKA9K8uDMpLWDcE/finding-before-funding-why-ea-should-probably-invest-more-in
- Menting, A. T., de Castro, B. O., & Matthys, W. (2013). Effectiveness of the Incredible Years parent training to modify disruptive and prosocial child behavior: A meta-analytic review. Clinical Psychology Review, 33(8), 901-913.
- Mesurado, B., Guerra, P., Richaud, M. C., & Rodriguez, L. M. (2019). Effectiveness of prosocial behavior interventions: a meta-analysis. In Psychiatry and neuroscience update (pp. 259-271). Springer, Cham.
- Pardey, P. G., Andrade, R. S., Hurley, T. M., Rao, X., & Liebenberg, F. G. (2016). Returns to food and agricultural R&D investments in Sub-Saharan Africa, 1975–2014. Food policy, 65, pp. 1-8.
- Plant, M. (2022). Don’t just give well, give WELLBYs: HLI’s 2022 charity recommendation. Effective Altruism Forum, https://forum.effectivealtruism.org/posts/uY5SwjHTXgTaWC85f/don-t-just-give-well-give-wellbys-hli-s-2022-charity
- Shin, J., & Lee, B. (2021). The effects of adolescent prosocial behavior interventions: a meta-analytic review. Asia Pacific Education Review, 22, 565-577.
- Silverman, B. W. (1986). Density estimation for statistics and data analysis (Vol. 26). CRC press.

As far as I can tell, ex-ante cost-effectiveness is not the most important figure for someone considering whether to fund a future project. I think the expected benefit per unit cost is more important.
For reference, you give this definition:
I think I understand what this means, but I am going to attempt to show why it's not that useful using a simple example.
Scenario 1: Suppose we know that a project will have benefit B=1 and that the projected cost C has distribution
P(C=1)=12
P(C=10)=12
Then the ex-post cost-effectiveness CE of the project will have distribution
P(CE=1)=12
P(CE=110)=12
and thus has expected value
E(CE)=12⋅1+12⋅110=0.505
Why is this not useful? It does not reflect the expected return-on-investment, and is not sensitive to high-cost scenarios. Consider Scenario 2, a similar project with known benefit B=1 and cost with distribution
P(C=1)=12
P(C=10000)=12
Scenario 2 is clearly much less cost-effective than Scenario 1. But the ex-ante cost-effectiveness is 0.500005, very close to 0.505.
What a decision-maker really wants to know is the amount of benefit they can expect from each unit of investment. This can be given byE(B)E(C).
Scenario 1: E(B)E(C)=15.5≈0.18
Scenario 2: E(B)E(C)=15000.5≈0.00020
We can see that this does appropriately reflect the difference in cost-effectiveness between the two scenarios. What I'm not so sure about is how we might give the expected benefit per unit cost as a distribution, rather than just a point-estimate.
It seems likely that I'm missing something.
Thank you for your feedback, Stan!
I think the appropriateness of E[CE] as a prioritization criterion depends on the nature of the decision problem.
I think the expected value of the cost-effectiveness ratio is the appropriate prioritization criterion for the following scenario: i) a decision-maker is considering which organization should receive a given fixed amount of money (m), and ii) each organization (i) turns every dollar it receives into some uncertain amount of value (CE_i). In that case, the expected utility of giving the money to organization i is E[U_i]= m*E[CE_i]. Therefore, the way to maximize expected utility is to give the money to the organization with the highest expected cost-effectiveness. In this scenario, the consequences of contributing $1 to a project with an expected cost-effectiveness of 1 WELLBY/$ are almost identical in both scenarios. Most of the expected utility comes from the possibility that the project might be highly cost-effective. If the project is not highly cost-effective, then the $1 contribution accomplishes very little, regardless of whether the project costs $10,000, $100,000, or $1,000,000.
In my view, your example illustrates that the expected cost-effectiveness ratio is an inappropriate prioritization criterion if the funder has to decide whether to pay 100% of the project's costs without knowing how much that will be. In that scenario, I think the appropriate prioritization criterion would be E[B]-E[CE_alt]*E[C], where E[CE_alt] is the expected cost-effectiveness of the most promising project that the funder could fund instead.
I think the second decision problem describes the situation of a researcher or funder who is committed to seeing their project through until the end. By contrast, the first decision problem corresponds to a researcher/funder intending to allocate a fixed amount of time/money to one project or another (e.g., 3 years of personal time or 1 million dollars) and then move on to another project after that.
Regardless thereof, I can rerun the analyses for E[B]/E[C] as a robustness check and let you know what I find.