This is a linkpost for the peer-reviewed article “Severe Global Cooling After Volcanic Super-Eruptions? The Answer Hinges on Unknown Aerosol Size” (McGraw 2024). Below are its abstract, my notes, my estimation of a nearterm annual extinction risk from supervolcanoes of 3.38*10^-14, and a brief discussion of it. At the end, I have a table comparing my extinction risk estimates with Toby Ord’s existential risk guesses given in The Precipice.
Abstract
Here is the abstract from McGraw 2024 (emphasis mine):
Volcanic super-eruptions have been theorized to cause severe global cooling, with the 74 kya Toba eruption purported to have driven humanity to near-extinction. However, this eruption left little physical evidence of its severity and models diverge greatly on the magnitude of post-eruption cooling. A key factor controlling the super-eruption climate response is the size of volcanic sulfate aerosol, a quantity that left no physical record and is poorly constrained by models. Here we show that this knowledge gap severely limits confidence in model-based estimates of super-volcanic cooling, and accounts for much of the disagreement among prior studies. By simulating super-eruptions over a range of aerosol sizes, we obtain global mean responses varying from extreme cooling all the way to the previously unexplored scenario of widespread warming. We also use an interactive aerosol model to evaluate the scaling between injected sulfur mass and aerosol size. Combining our model results with the available paleoclimate constraints applicable to large eruptions, we estimate that global volcanic cooling is unlikely to exceed 1.5°C no matter how massive the stratospheric injection. Super-eruptions, we conclude, may be incapable of altering global temperatures substantially more than the largest Common Era eruptions. This lack of exceptional cooling could explain why no single super-eruption event has resulted in firm evidence of widespread catastrophe for humans or ecosystems.
My notes
I have no expertise in volcanology, but I found McGraw 2024 to be quite rigorous. In particular, they are able to use their model to replicate the more pessimistic results of past studies tweeking just 2 input parameters (highlighted by me below):
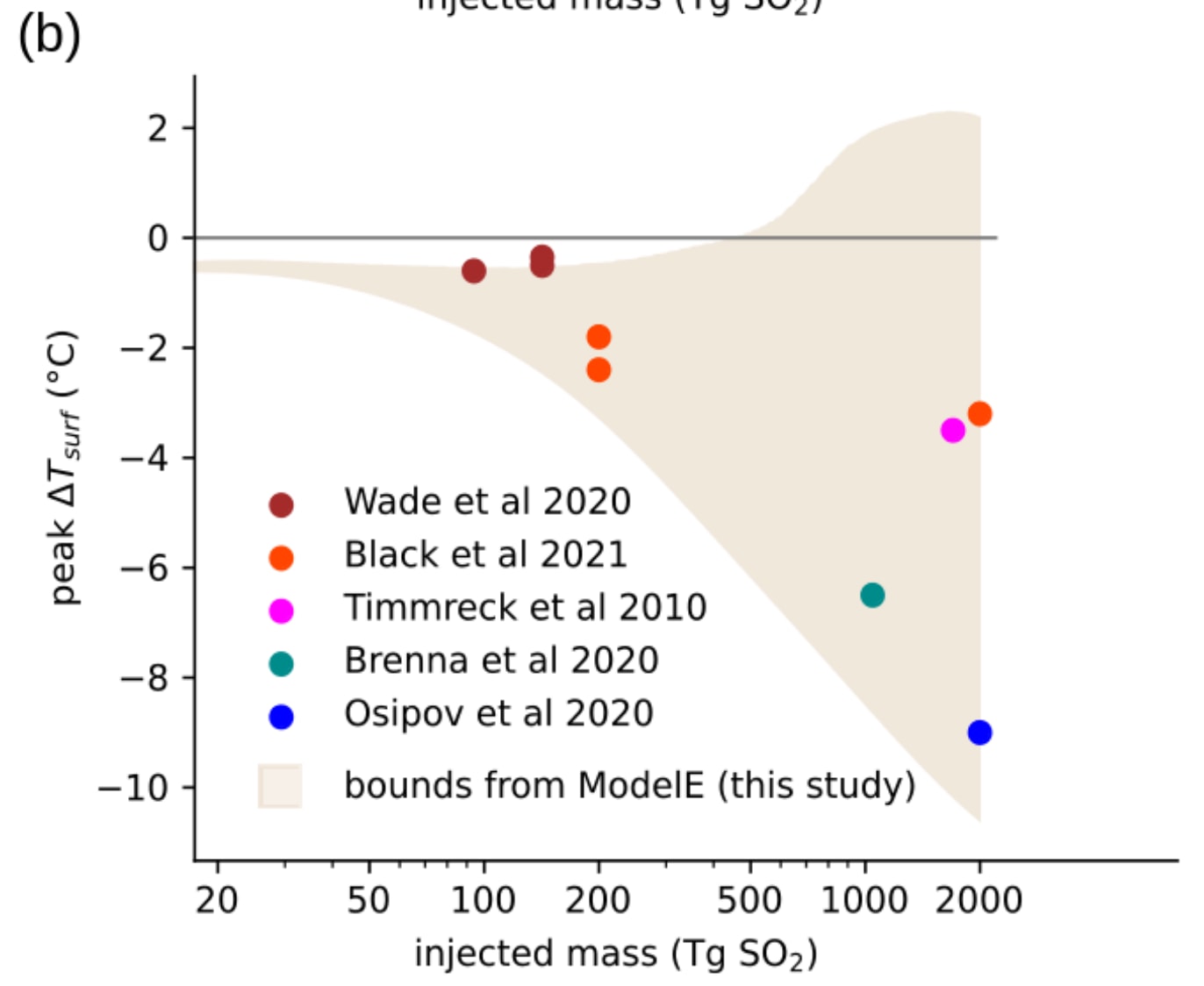
- “We next evaluate if the assessed aerosol size spread is the likely cause of disagreement among past studies with interactive aerosol models. For this task, we interpolated the peak surface temperature responses from our ModelE simulations to the injected mass and peak global mean aerosol size from several recent interactive aerosol model simulations of large eruptions (Fig. 7, left panel). Accounting for these two values alone (left panel), our model experiments are able to reproduce remarkably similar peak temperature responses as the original studies found”. By “reproduce remarkably well”, they are referring to a coefficient of determination (R^2) of 0.87 (see Fig. 7).
- “By comparison, if only the injected masses of the prior studies are used, the peak surface temperature responses cannot be reproduced”. By this, they are referring to an R^2 ranging from -1.82 to -0.04[1] (see Fig. 7).
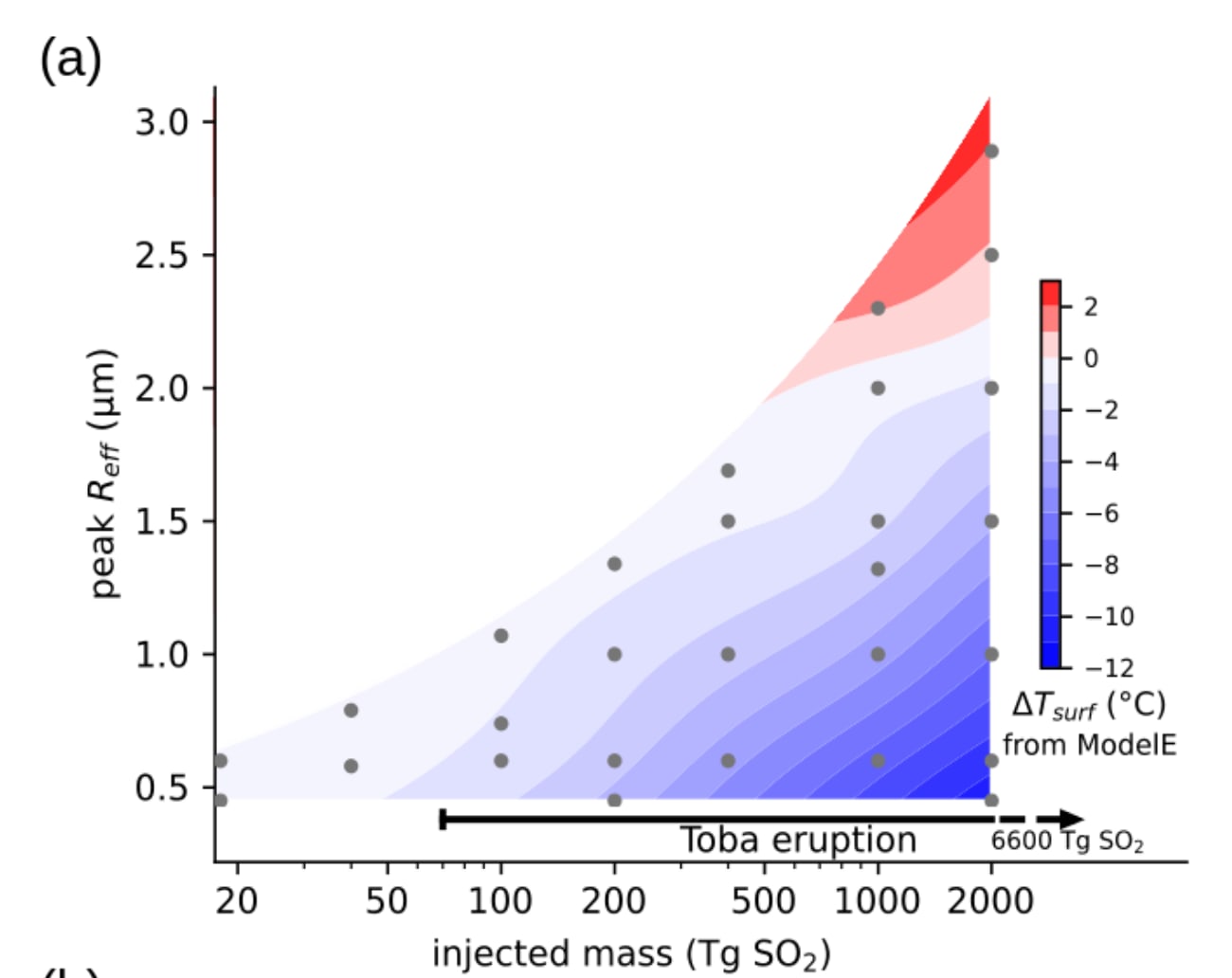
They agree with past studies on the injected mass, but not on the aerosol size[2]. Fig. 3a (see below) illustrates the importance of the peak mean aerosol size. The greater the size, the weaker the cooling. I think this is explained as follows:
- Primarily, smaller particles reflect more sunlight per mass due to having greater cross-sectional area per mass[3].
- Secondarily, larger particles have less time to reflect sunlight due to falling down faster[4].
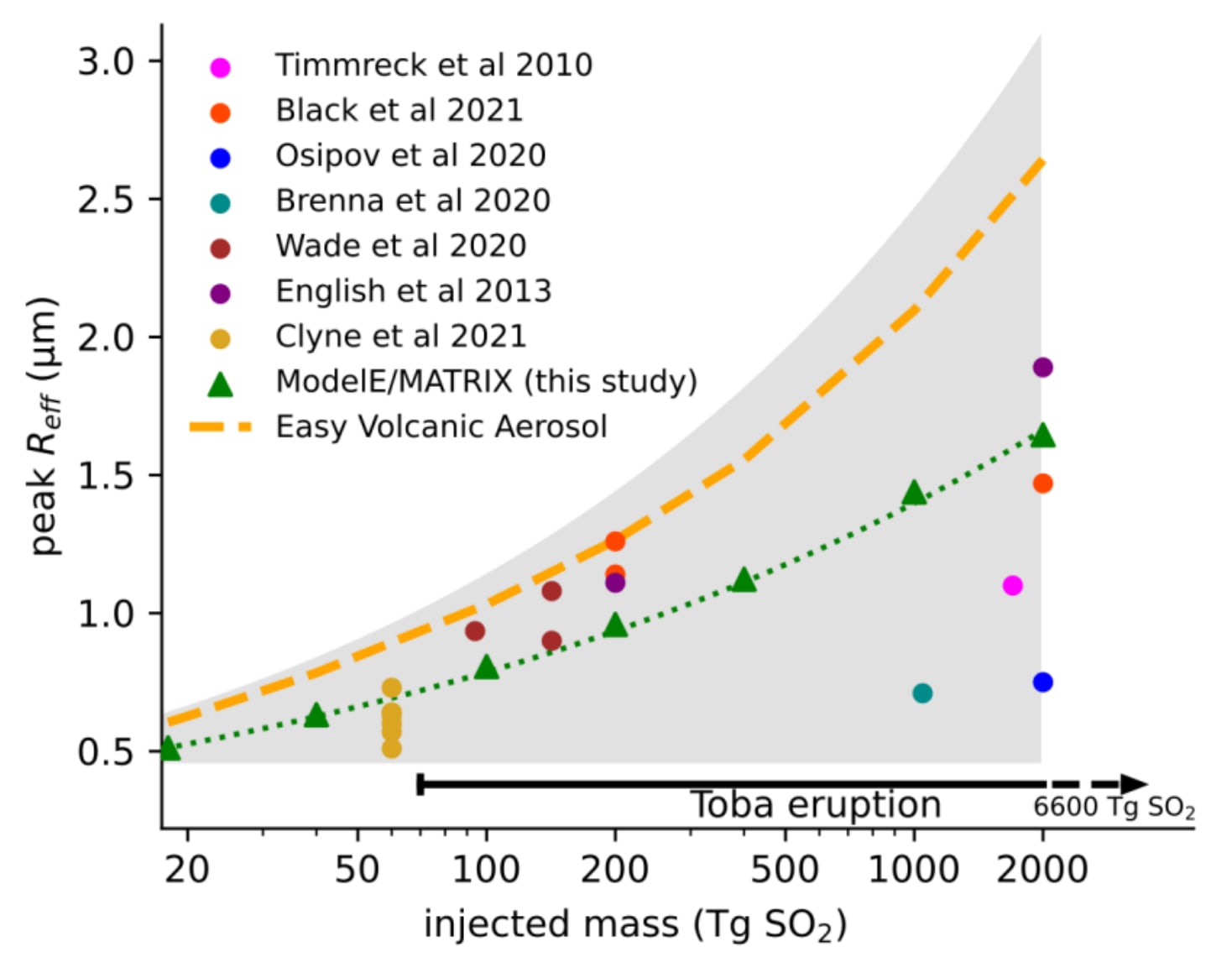
According to Fig. 2 (see below), aerosol size increases with injected mass, which makes intuitive sense. So we are lucky big eruptions have less cooling potential per injected mass. For context, the 1815 eruption of Mount Tambora injected 56 Tg of sulphur dioxide (SO2) into the stratosphere (from Table 1 of Wolff 2023), and had a volcanic explosivity index (VEI) of 7.
Past studies have used a small aerosol size for large eruptions, so they estimated much greater cooling than McGraw 2024. This says the following on the relationship between injected mass and aerosol mass:
- “While a power law scaling (Eqn. 1) is a common assumption, we are aware of only one study that tested this relationship with interactive aerosol models (Aubry et al. 2020), and no study that specifically compared different eruption realizations (rather than different months within simulations) or included injection masses >100 Tg SO2”.
- “Therefore, to test the validity of the power law functional form we ran GISS ModelE with the MATRIX interactive aerosol model (Bauer et al. 2008, 2020) over a wide range of SO2 injection masses”.
- “Our results confirm that a power law emerges, with peak global mean effective radius values (green triangles in Fig. 2) closely following a k=1/4 power law fitting to injected mass (dashed green line in Fig. 2)”.
This green line predicts larger aerosol size than most past studies for large eruptions (see figure just above).
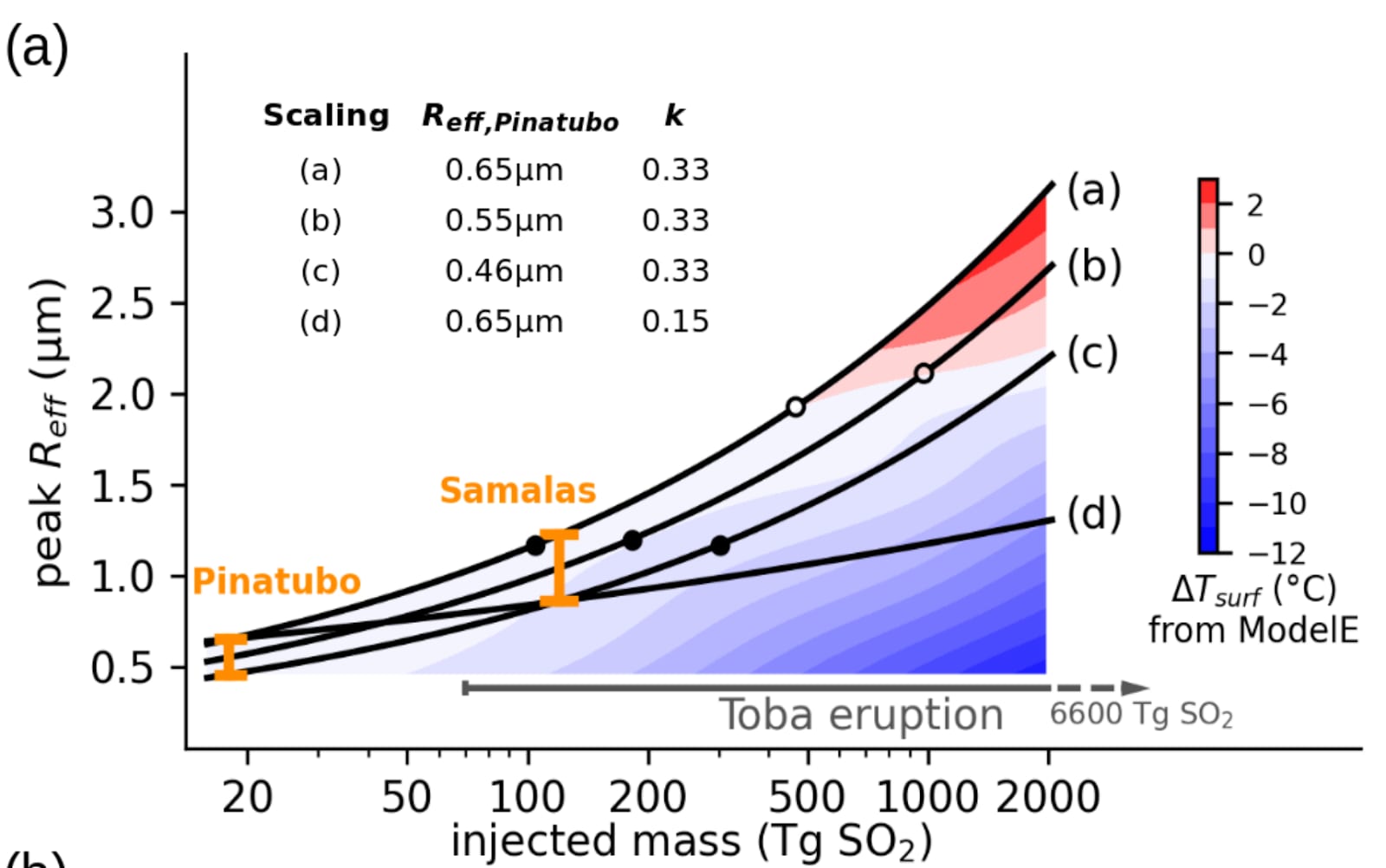
Fig. 10 is pretty crucial to McGraw 2024’s conclusion of 1.5 ºC maximum cooling. In Fig. 10a (see below), they define 4 potential scalings based on the aerosol size of the eruptions of Pinatubo and Samalas:
- (a) is defined by their upper bounds, so it is optimistic. It overestimates the constant of proportionality, and therefore overestimates aerosol size, and underestimates cooling.
- (b) is defined by the means of their aerosol size (their best guess). “As scaling (b) traverses the mean of both our Pinatubo and Samalas Reff bounds, we treat this as our best estimate for how aerosol size scales with injection mass”.
- (c) is defined by their lower bounds, so it is pessimistic. It underestimates the constant of proportionality, and therefore underestimates aerosol size, and overestimates cooling.
- (d) is defined by the upper bound of Pinatubo (smaller eruption), and lower bound of Samalas (larger eruption), so it is very pessimistic. It underestimates the exponent of the power law, and therefore greatly underestimates aerosol size, and greatly overestimates cooling.
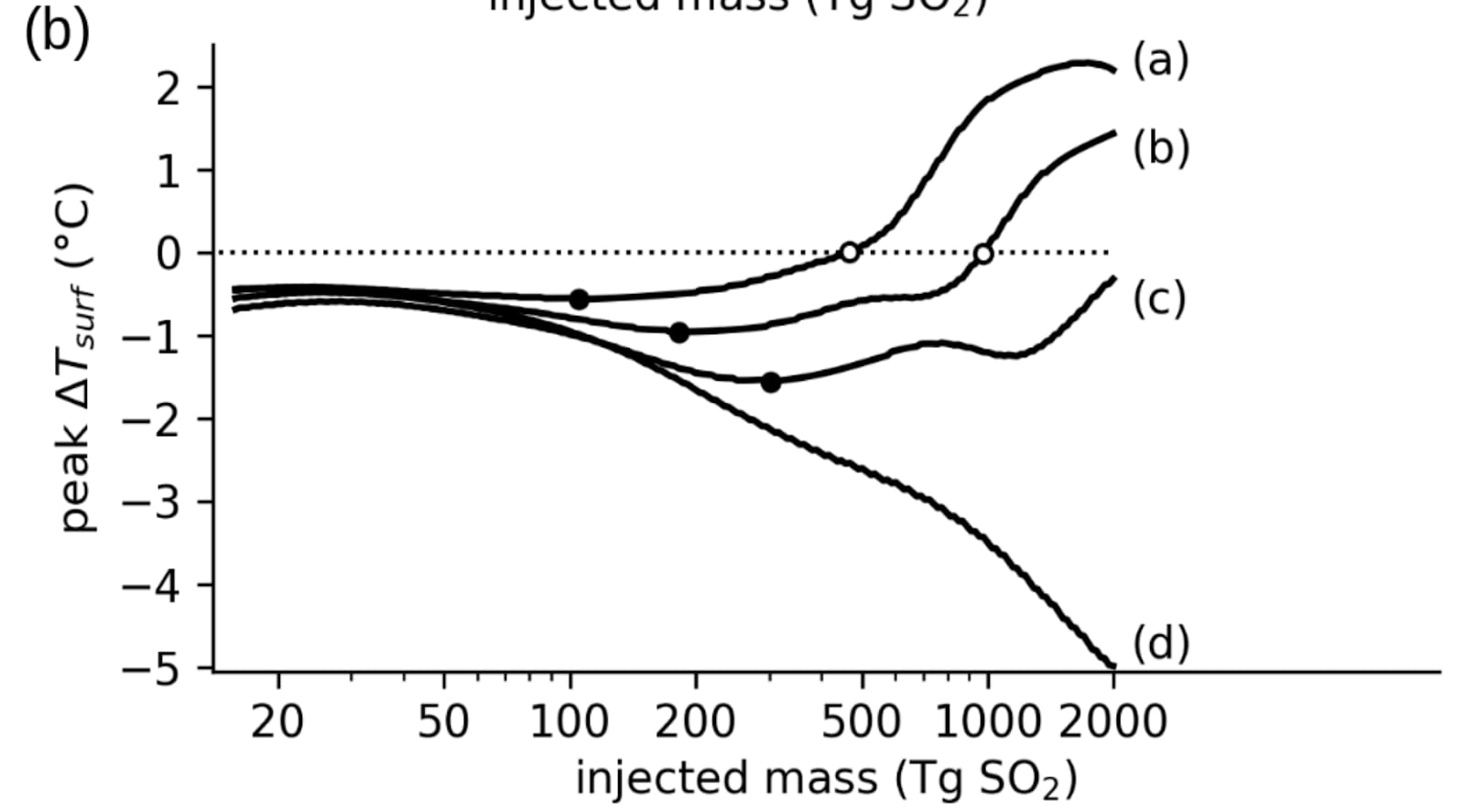
Figure 10b (see below) shows the cooling for the various levels of scaling. The maximum cooling is:
- 0.5 ºC for their optimistic aerosol size (a).
- 1 ºC for their best guess aerosol size (b).
- 1.5 ºC for their pessimistic aerosol size (c). This is the number they mention in the abstract.
- 5 ºC for 2 k Tg of SO2 and their very pessimistic aerosol size (d). 2 k Tg is the mass injected into the stratosphere in the Toba eruption (see Table 1), which some argue almost caused human extinction.
Extinction risk from supervolcanoes
Calculations
I calculated a nearterm annual extinction risk from supervolcanoes of 3.38*10^-14 (= 3.38*10^-8*10^-6). By nearterm annual risk, I mean that in a randomly selected year from 2025 to 2050. I got my estimate multiplying:
- 3.38*10^-8 (= 2.5*10^-3*1.35*10^-5) annual probability of an eruption causing a maximum surface cooling of at least 5 ºC. I computed this from the product between[5]:
- 0.25 % (= 0.05^2) chance of a more pessimistic relationship between injected mass and aerosol size than the suggested by curve (d) of Fig. 10b of McGraw 2024, assuming a probability of 5 % of the power law being defined by:
- Greater aerosol mass than the upper bound of Pinatubo.
- Smaller aerosol mass than the lower bound of Samalas.
- 0.00135 % (= 1/(74*10^3 + 2)) annual chance of an eruption worse than Toba’s, which was 74 k years ago. I just applied Laplace’s rule of succession, but I guess there is research estimating the probability of an eruption as a function of the minimum injected mass of sulphur dioxide into the stratosphere.
- 0.25 % (= 0.05^2) chance of a more pessimistic relationship between injected mass and aerosol size than the suggested by curve (d) of Fig. 10b of McGraw 2024, assuming a probability of 5 % of the power law being defined by:
- 10^-6 probability of human extinction given a maximum surface cooling of at least 5 ºC:
- I have assumed before a probability of 10^-6 of human extinction given insufficient calorie production, considering 1 M years is the typical lifespan of a mammal species[6]. I defined insufficient calorie production as less than 1.91 k kcal/person/d, and I guess the aforementioned maximum surface cooling would result in a similar calorie production.
- Eyeballing Figure 3 of Toon 2014, a maximum surface cooling of 5 ºC corresponds to a nuclear winter involving 63.1 Tg (= 10^1.8) of soot injected into the stratosphere.
- Supposing the net effect on calorie production of all the adaptation measures is similar to assuming equitable food distribution, consumption of all edible livestock feed, and no household food waste, linearly interpolating the data of Fig. 5a of Xia 2022, 63.1 Tg leads to a calorie consumption of 2.18 k kcal/person/d (= 2.38 - (2.38 - 1.08)/(150 - 47)*(63.1 - 47)), which is 1.14 (= 2.18*10^3/(1.91*10^3)) times the threshold for insufficient calorie assumption.
- For context, the aforementioned maximum surface cooling would result in temperatures similar to those of the last ice age temperatures. From NOAA, “the latest ice age peaked about 20,000 years ago, when global temperatures were likely about 10°F (5°C) colder than today”.
- I have assumed before a probability of 10^-6 of human extinction given insufficient calorie production, considering 1 M years is the typical lifespan of a mammal species[6]. I defined insufficient calorie production as less than 1.91 k kcal/person/d, and I guess the aforementioned maximum surface cooling would result in a similar calorie production.
Discussion
Relative to what I obtained for other risks, my nearterm annual extinction risk from supervolcanoes of 3.38*10^-14 is:
- 1.54 (= 3.38*10^-14/(2.20*10^-14)) times mine for asteroids and comets.
- 0.570 % (= 3.38*10^-14/(5.93*10^-12)) of mine for nuclear war.
- 3.38*10^-9 (= 3.38*10^-14/10^-5) of mine for artificial intelligence (AI).
Note supervolcanoes might have cascade effects which lead to civilisational collapse, which could increase longterm extinction risk while simultaneously having a negligible impact on the nearterm one I estimated. I do not explicitly assess this in the post, but I guess the nearterm annual risk of human extinction from supervolcanoes is a good proxy for the importance of decreasing volcanic risk from a longtermist perspective:
- Supervolcanoes might have cascade effects, but so do other catastrophes.
- Global civilisational collapse due to supervolcanoes seems very unlikely to me. There would be global impacts via volcanic ash, but I guess infrastructure loss would be more significant for a similarly likely nuclear war.
- Even if a volcanic eruption causes a global civilisational collapse which eventually leads to extinction, I guess full recovery would be extremely likely. In contrast, an extinction caused by advanced AI would arguably not allow for a full recovery.
- Appealing to cascade effects or other known unknowns feels a little like a regression to the inscrutable, which is characterised by the following pattern:
- Arguments for high existential risk initially focus on aspects of the risk which are relatively better understood (e.g. famine deaths due to the climatic effects of nuclear war).
- Further analysis frequently shows the risk from such aspects has been overestimated, and is in fact quite low (e.g. nearterm risk of human extinction from nuclear war).
- Then discussions move to more poorly understood aspects of the risk (e.g. how the indirect effects of supervolcanoes affect the longterm values of transformative AI).
In any case, I believe interventions to decrease deaths from supervolcanoes should be assessed based on standard cost-benefit analysis (CBA):
- Having in mind my astronomically low nearterm annual extinction risk from supervolcanoes, it is unclear to me whether interventions to decrease deaths from supervolcanoes decrease extinction risk more cost-effectively than broader ones, like the best interventions to boost economic growth or decrease disease burden (e.g. GiveWell’s top charities).
- I expect extinction risk can be decreased much more cost-effectively by focussing on AI risk rather than supervolcanoes risk (relatedly). So I would argue interventions to decrease deaths from supervolcanoes can only be competitive under an alternative worldview, like ones where the goal is boosting economic growth or decreasing disease burden.
Moreover, I would propose using standard CBAs not only in the political sphere, as argued by Elliott Thornley and Carl Shulman, but also outside of it. In particular, volcanic risk would be significantly more prioritised by grantmakers aligned with effective altruism if it is concluded that the best interventions to decrease it save lives more cost-effectively than GiveWell’s top charities.
Comparison between Toby Ord’s existential risk and my extinction risk
I collected in the table below Toby Ord’s annual existential risk from 2021 to 2120 from AI, nuclear war, supervolcanoes, and asteroids and comets based on his guesses given in The Precipice. I also added my estimates for the nearterm annual extinction risk from the same 4 risks, and the ratio between Toby’s values and mine. The values are not directly comparable, because Toby’s refer to existential risk and mine to extinction risk. Nonetheless, I still have the impression Toby greatly overestimated tail risk. This is in agreement with David Thorstad’s series exaggerating the risks, which includes subseries on climate, AI and bio risk, and discusses Toby’s book The Precipice.
Risk[7] | Toby’s annual existential risk from 2021 to 2120[8] | My nearterm annual extinction risk | Ratio between Toby’s value and mine |
AI | 0.105 % | 105 | |
Nuclear war | 1.00*10^-5 | 1.69 M | |
Supervolcanoes | 1.00*10^-6 | 3.38*10^-14 | 29.6 M |
Asteroids and comets | 1.00*10^-8 | 455 k |
Acknowledgements
I did the initial investigation for this post as part of a project funded by Nuño Sempere's research consultancy Shapley Maximizers, for which I worked as a contractor to assess the impact of The Centre for the Study of Existential Risk (CSER); thanks Nuño. Thanks to Anonymous Person 1 and Anonymous Person 2 for feedback on the draft.
- ^
Note the R^2 can be arbitrarily negative because one can make arbitrarily bad predictions.
- ^
“An aerosol is a suspension of fine solid particles or liquid droplets in air or another gas”.
- ^
The cross-sectional area of a sphere is proportional to its radius to the power of 2, whereas its mass is proportional to its radius to the power of 3, so its cross-sectional area per mass is inversely proportional to its radius.
- ^
Drag is proportional to area, and mass is proportional to volume, so the deceleration from drag is inversely proportional to the size (holding the drag coefficient and speed constant). In turn, this means larger particles will tend to be less decelerated by air, and therefore fall faster. In a vacuum, falling time does not depend on mass nor shape.
- ^
For reference, McGraw 2024 “deem cooling beyond 5°C highly unlikely”.
- ^
Humans are a mammal species.
- ^
Ordered from the largest to the smallest.
- ^
“Annual risk” = 1 - (1 - “total risk”)^(1/“duration of the period in years”). The period has a duration of 100 years (= 2120 - 2021 + 1).

Hi there, Volcanologist here. Firstly, thanks for making the effort to look into this area and engage with it.
TLDR: I agree that extinction risk from volcanic risk is extremely extremely low*… (*on its own). But this post comes up with a single probability number, based on one new (and not yet established) paper based on playing about with climate model parameters. You could do a dive into another volcano-climate paper and get a completely different view of impacts e.g. https://iopscience.iop.org/article/10.1088/2752-5295/acee9f/meta. In fact, you could also see this same paper from a different side and say that it could increase the x-risk factor, by (depending on what aerosol size you pick and choose) heating the earth and driving rapid warming on top of Anthropogenic warming. Does this mean that we should not worry about volcanic eruptions as contributing to existential risk? My answer would be no.
To suppose that you can predict (and put a probability value) on what the societal reactions and subsequent decisions made, the interaction between other risks (AI, wars, pandemics etc) and geo-political landscape and actions would be when faced with the impacts of a large volcanic eruption (note that I say large and not super-eruptions- cause we’re not just talking about super eruptions here), seems overly reductionist and simplistic to me. For instance, When faced with the starvation of hundreds of millions of people (if not billions- though I think that study overestimates agricultural loss), as well as droughts and other extreme weather events (failure of monsoons etc), energy security, financial loss of tens of trillions etc, and knowing that often it’s the state of the world (e.g. vulnerability, inequality) and the geopolitical reactions to that risk, that really control whether the risk could be minimised through global governance cooperation and preparedness actions, or whether humanity’s reactions to such risks (e.g. banning exports) may worsen the initial risk considerably, as well as cascading risks. So for me, judging how volcanic eruptions contribute to civilisation collapse or x-risk needs to incorporate these factors, This post does not engage with this, and bases their numbers on one paper and has extrapolated using non-rigorous constriants.
Point about the paper itself:
I asked my climate science colleague about the paper and they had a lot of uncertainty on on how much trust we should place on this: “I would be wary about taking this 1.5C as ground truth...Lots of disagreement between our models, and lots of processes they don't account for yet (e.g. halogen, water, injection height, time of eruptions, eruption time frame). The proxy record is always tricky as it's a mix of forced response and natural variability, and not a full global picture. My understanding is also that if anything, tree ring underestimate peak cooling because they integrate the response a bit. So I don't think they reliably support or don't support this limit.”
“Models with interactive stratospheric aerosols have been telling us for ~15 years that aerosol growth would strongly limit the cooling after very large events. There might be disagreement on maximum aerosol radius/cooling because there is still a large uncertainty in stratospheric aerosol modelling (Clyne et al 2021)”
A few of my own thoughts about the same paper Vasco cites:
- We really don’t understand aerosol size at all, let alone for smaller eruptions (For example, In smaller eruptions, aerosol size change throughout eruptions and we don’t know why this is yet (link: https://acp.copernicus.org/articles/23/9725/2023/)), and so we have an even poorer grasp on aerosol size for bigger eruptions (they say as much in the paper- and as much as anything-the paper advocates for more experiment studies- I totally agree).
- Published proxy records record greater cooling than 1.5 degrees (mostly summer cooling and mostly based in Northern hemisphere- but that’s where the tree records are), e.g. the 540 eruption. So while it’s possible that 1.5 degrees is the limit, based on this smaller eruption exceeding that limit, it seems unlikely.
- Eruptions often do not erupt all their Sulfur in one go, and super eruptions especially likely last years and will be separated by breaks in activity, this periodicity mostly certainly affects the aerosol size- this doesn’t seem to be mentioned at all.
General points:
But your point about extinction risk being very low is mostly right, though you can do the same by diagnosing the statistics (super eruptions occur every 17,000 years or so, so it’s unlikely that humans would go extinct as we haven’t done previously 300,000 years). But there’s some more complicated caveats to this:
- We’ve never experienced one since human civilisations started ~12,000 years ago, the last one was 26,000 ago in New Zealand, and let alone since modern interconnected, globalised society.
- Since then we’ve globalised the food trade, and its susceptible to harvest fails if all grown in certain breadbaskets, and hydroclimate extreme events following eruptions make this far more likely (see paper cited above), not to mention trade choke points.
- Saying this the conclusion that volcanic eruptions cannot lead to human extinction* (*on its own). This is where it get a bit more complicated, and often analyses like this and Toby Ord’s analyses feel too reductionist and simplistic. For instance, many societal collapses in previous history (many coincide with eruptions), but they are rarely due to one factor alone. However if you were to take out say catastrophic volcanic eruptions, then they would likely not happen at all.
- This is also apparent when we look at major collapses, which don’t always correlate with the largest climatic impacts, so the idea that you approximate existential threat based on the magnitude of the effects seems a bit of a strawman case for these reasons. This effect is accentuated by the regional impacts to breadbaskets or physical blocking of trade routes via direct volcanic material- this means that location of the eruption is super important too, not just the magnitude. Vulnerability, reactions and other compounding risks (wars, inequality etc) turn out to be much more important. The logic of Ord et al to assess one risk in isolation is not realistic and the numbers he generates have very little meaning in the real world.
In general, explosive volcanic eruptions will never be the sole cause for extinction, but they could be very meaningful in increasing existential risk factor, so that once another big risk(s) comes along they have increased the vulnerability to that threat, where we might have otherwise come through it without the eruption.
Finally this quote it makes it hard for me to relate with this wing of the Effective Altruism community:
Irrespective of extinction risk - should we care (and do something) about that fact that large volcanic eruptions could threaten the lives and livelihoods of billions, and this is for a risk that has a 1 in 6 per century probability?
Perhaps I'm in an alternative/more isolated worldview- but I would say yes.
Thanks for following up, Michael!
... (read more)