This is the fifth and final post in a series. Here are the first, second, third, and fourth posts.
Appendix
Appendix table of contents:
1: Pros and cons of probability-focused solutions
1.1: Argument from hypothetical updates
1.2: Argument from complexity and computability
2: Pros and cons of the bounded utility solution (and the related solution of having a steeply-diminishing but unbounded utility function)
3: On the “cancelling out” strategy and the connection to the cluelessness debate
4: On rejecting expected utility maximization
4.1: On the “Law of Large Numbers” defense of expected-utility maximization and its implications for long-termist projects
5: Act-focused vs. world-focused graphs and the implications for long-termism
1: Pros and cons of probability-focused solutions
This subsection explains what it would take to have a probability function that doesn’t lead to funnel-shaped action profiles, and the merits and drawbacks of doing so.
First, why is it so hard to avoid funnel-shaped action profiles without being closed-minded? What reason do we have to think that the utilities rise faster than the probabilities shrink, in the long run?
There are several arguments. First, there’s the previously-mentioned argument from hypothetical updates. This was an argument that a particular possibility—saving 10^10^10^10 lives by giving $5 to Pascal’s Mugger—had a probability much higher than 0.1^10^10^10. It seems that we can generate more and more outlandish possibilities and then repeat this argument for each of them. See section 1.1 for this argument in more detail.
Second, there are some more abstract arguments. If the prior probability of a hypothesis is a computable function of its complexity (rather than, say, a function of both its complexity and utility) then as you consider more and more hypotheses, the utilities will grow faster than the probabilities can shrink. (See 1.2) Relatedly, there’s a proof that for the special case of perception-determined unbounded utility functions, open-mindedness implies every action has undefined expected utility. (de Blanc 2007) (That said, that proof might not generalize much, since perception-determined utility functions are weird.)
Third, there is the argument from objective chance and St. Petersburg games developed by Hájek and Smithson (2012). Consider a modified St. Petersburg game in which the payoffs are 2^10^N instead of 2^N. If you are open-minded, then you’ll assign some positive probability to the hypothesis “If I do action A, that will trigger the playing of a modified St. Petersburg Game.” This hypothesis further subdivides into infinitely many possible outcomes of doing action A, one for each outcome of the resulting game. Since each possible outcome of playing this game contributes many times more to the total expected value of the action than the previous one, and yet is precisely half as probable, the action profile as a whole will be funnel-shaped.
Finally, we still have to decide what to do with infinitely valuable outcomes. If we assign positive probability to any of them, they will swamp everything else in our expected utility calculations. (Beckstead p143) We could deal with such outcomes separately, but it would be nice to have a unified solution.
Considering the above, one response (taken by e.g. Hájek) is to give up on open-mindedness/regularity. We can avoid our problems if we assign probability 0 to all of the troublemaking possibilities—perhaps we refuse to countenance anything which involves extra dimensions, or sufficiently large coincidences, or things like that. Perhaps we take a normal open-minded probability function and then truncate it by ignoring everything past a certain point on the chart.
Rejecting open-mindedness is bad for two reasons: First, open-mindedness ensures that you’ll never assign probability 0 to the truth. Second, it’s nice to be able to appeal to a deep and plausible theory to justify your beliefs. Theories like Solomonoff Induction, for example, give guidance on what probabilities to assign, and they say to be open-minded. By contrast, it seems that assigning probability 0 to any set of possibilities diverse enough to avoid funnel-shaped action profiles will be arbitrary and ad hoc, resulting in intractable and subjective disagreements. Third, as Beckstead points out, there are some current theories in physics which entail that we could eventually produce infinitely many happy lives. To avoid all our problems by rejecting open-mindedness, we would have to assign probability 0 to those theories.
Despite all these issues, this category of solution to the problem still has its advocates—most notably Hájek and Smithson (2012) and Smith (2014).
1.1: Argument from hypothetical updates
This section presents my version of an argument I first saw here. Recall the first half of the argument, given in section 2, having to do with a hypothetical situation in which the Mugger pulls you through what appears to be an interdimensional portal and takes you on an adventure...
Let Pnew() be your credence function after undergoing the multi-day adventure. Let P() be your credence function at the beginning, when the Mugger makes his offer. Let BB be the hypothesis that the world is as our mainstream theories of physics says it is, and moreover that you are a Boltzmann Brain that randomly fluctuated into existence. (See https://arxiv.org/abs/1702.00850v1 explanation of what a Boltzmann Brain is. I’m choosing this instead of “hallucination” because we can more precisely quantify its probability, and because it’s an even lower-probability event than hallucination, thus making the argument even stronger.)
Let TT be the hypothesis that Pascal’s Mugger is telling the truth, i.e. that the laws of physics are different and allow for travel between dimensions, etc. Your evidence, E, is the multi-day adventure that you experience.
Suppose that, after your adventure, you are more confident that the Mugger is telling the truth than that you are a Boltzmann Brain hallucinating it all. That is, suppose that . Then that means
If you obey Bayes’ Rule, then Pnew() is the result of conditionalizing P() on E. So: .
We can (very roughly) estimate and :
P(E|BB) ≈ 1/(2^10^12) because your adventure gives you about 10 bits of information or so, meaning that the probability of your adventure being generated randomly by thermodynamic fluctuations (assuming you are a BB) is 1/(2^10^12).
P(BB) ≈ 1/(e^10^66) because that’s the probability of a given chunk of matter in vacuum coming together to form a Boltzmann Brain in exactly the same state as you (Carroll 2017).
Putting it all together, assume (conservatively) that P(E|TT) = 1. Even in that case, we see that P(TT) > 1/(10^10^10^10). (Otherwise, , contradicting our assumption that .)
Note that nothing much hangs on these estimates. If you think that you know you aren’t a Boltzmann Brain, for example, because you think you know that you have hands and friends and an evolutionary history—then fine, imagine a Boltzmann Star System instead. Much bigger, and therefore much less likely to spontaneously assemble—maybe 1/(e^10^100). But 1/(10^10^10^10) is a very small number. And remember that we can always change the example to make the number promised by the Mugger even bigger.
The conclusion is that if you follow normal Bayesian updating (and assign non-negligible probability to Boltzmann Brains being possible, i.e. to our theories of physics being approximately correct), you either think that the probability that the Mugger is telling the truth is higher than 0.1^10^10^10, or you think it is so unlikely that you would continue to think it less likely than the incredibly-unlikely Boltzmann Brain scenario even if you spent the rest of your life adventuring with him through different dimensions exactly as he predicted.
1.2: Argument from complexity and computability
Assume you are open-minded. Assume your utility function is computable and unbounded. Assume your prior probability function of a hypothesis is a computable function of its complexity.
Consider the hypotheses of the form “And then a magic genie creates an outcome of value equal to the result of program X.” Since you are open-minded and your utility function is computable and unbounded, there will be one such hypothesis for every such X that halts. Now, X is the only variable in the above, so hypotheses of that form will have a complexity that equals the complexity of X plus some constant. Imagine lining up all these programs by complexity, from simplest to most complicated.
One reasonable interpretation of Occam’s Razor is that as we travel down the line, we should shrink the probabilities by some computable function—one standard idea is to make the probabilities a logarithm of the complexity, but in principle you could have a stricter or looser complexity penalty. Meanwhile, the utilities of these genie-hypotheses will grow at the rate of the Busy Beaver function, which grows faster than any computable function. So probabilities that result from pure Occam’s Razor, when combined with unbounded computable utility functions, create funnel-shaped action profiles.
Perhaps our probabilities should not result from pure Occam’s Razor. Obviously our evidence should be involved somehow, but this doesn’t fix things if the hypotheses in the above set are consistent with our evidence. Perhaps in addition to Occam’s Razor we should also have some other virtues that our theories are judged by. In principle this could fix the problem—for example, if we imposed a “leverage penalty” that made hypotheses less likely to the extent that they involve us having larger opportunities to do good. (I don’t think the leverage penalty will work. See bibliography for links to discussions of it.) However, it’s hard to think of any independent motivation for penalizing large opportunities for good, and at any rate there are still the other arguments to deal with.
2: Pros and cons of the utility-focused solution
This subsection discusses another way to handle tiny probabilities of vast utility: Use a bounded utility function.
A utility function judges how good an outcome is by assigning a number to it. The examples and illustrations used so far in this paper have assumed a simple one-to-one conversion between happy lives saved and utility: They assigned utility X to an outcome in which the contemplated action saves X happy lives. A bounded utility function takes a more complicated approach. For our purposes, a bounded utility function has a limit on how good or bad things can be. It never assigns numbers higher than B or lower than -B, for some finite B. Visually, this would look like two horizontal lines on our graph, between which every star must be placed. As a result, possible outcomes of probability less than 1/B will contribute less than 1 to the total expected utility of the action, those less than 1/(10B) will contribute less than 0.1 to the total, and so on. Though the action profile might still look like a funnel in the early stage, it is guaranteed to be bullet-shaped once you approach the bound, and it is guaranteed to converge to some finite expected value even when all possibilities are considered.
One way to bound our utility function (with respect to lives saved) would be to convert happy lives saved to utility at a rate of one to one, until you reach B, at which point each additional happy life saved adds nothing to the overall utility. (We’d have to say similar things for the other metrics that we might care about, such as years of life lived, amount of knowledge gained, amount of injustice caused, etc.) This is not a popular approach, because intuitively it’s always better to save more lives, other things equal.
A more popular way to bound the utility function is to assign diminishing marginal utility to the things that matter. For example:

The major versions of utilitarianism seem to imply that we should use unbounded utility functions. For example, classical utilitarianism says that saving a happy life is equally valuable whether it is the only life being saved, or one of 10^10^10^10. So saving 10^10^10^10 happy lives is 10^10^10^10 times as good as saving one happy life. This reasoning appeals even to many people who reject utilitarianism: If the number of other people involved doesn’t matter to the people being saved, why should it matter to you? Hence, bounding the utility function is unappealing to many people.
In defense of bounded utility functions, it seems that lots of things that matter to us have diminishing marginal utility. For example, we like having friends, but having 1000 friends is less than 100 times better than having 10 friends. Perhaps everything is like this. (But as long as there is at least one thing that is not like this, our utility function will be unbounded.)
Also, the intuitive appeal of unboundedness seems strong in cases involving normal numbers but weak in cases involving extreme numbers. For example, many people feel that it would be foolish to give up a 0.99999 chance of everyone living happily for a trillion years for a 0.1^100 chance of everyone living happily for N years, no matter how high N is. Yet a utility function that is unbounded (with respect to years of life lived) would recommend the second option if N is high enough.
On the other hand, there are cases that pull many intuitions in the opposite direction. For example, if you have a bounded utility function and were presented with the following scary situation: “Heads, 1 day of happiness for you, tails, everyone is tortured for a trillion days” you would (if given the opportunity) increase the stakes, preferring the following situation: “Heads, 2 days of happiness for you, tails, everyone is tortured forever.” (This particular example wouldn’t work for all bounded utility functions, of course, but something of similar structure would.)
From a different angle, some people have criticized this solution as unsatisfying, because it leaves people who have unbounded utility functions out in the cold. The thought is that rationality doesn’t tell us what utility function to have, it just tells us what to do with it once we have it. There must be some rational response to Pascal’s Mugging, the Pasadena Game, etc. for people with unbounded utility functions, and whatever that response is, we should consider adopting it for ourselves as well even if we have unbounded utility functions.
There is a lot more to say about the pros and cons of adopting a bounded utility function; for further reading see e.g. Parfit (1986), Beckstead (2013), Bostrom (2011), and Smith (2014).
It’s possible to solve the problem with an unbounded utility function if it has sufficiently extremely steeply diminishing returns. (To do this your utility function may have to be uncomputable; see section 1.2.) Anyhow, if your utility function has diminishing returns that steep, it faces most of the same worries and counterintuitive implications as having a strict bound.
3: On the “cancelling out” strategy and the connection to the cluelessness debate
In the literature there is a problem called “Cluelessness” which is somewhat related to Pascal’s Mugging. (Lenman 2000) It goes like this:
It is a fairly undisputed fact that the short-term effects of our actions—e.g. helping Grandma across the street makes her happy—pale in comparison to the long-term effects, e.g. on when and where hurricanes strike years later, on the DNA of future children, etc. This is thought by many to be a source of problems for consequentialists. For example, how are slogans like “Do the most good” supposed to be helpful to us, if we have no clue whether helping Grandma across the street will do more good than harm?
(One part of) the standard response is to say that we should do the best we can given our uncertainty, and to cash that out as maximizing expected utility. Once we’ve said this, we can wriggle out of the problem by pointing out that we have exactly as much reason to think that helping Grandma across the street will cause a hurricane as we have to think that not helping Grandma across the street will cause a hurricane. And the same goes for all the other far-flung but unpredictable effects; the DNA of future children, for example, is determined by a process relevantly similar to drawing a ball at random from an urn. So the thought is that the long-term effects about which we are clueless will cancel out neatly; the long-term effects about which we are not clueless should rightly be considered. (If we really did have reason to think that e.g. agitating the air at this particular intersection increased the chances of a hurricane years from now, then fine, we shouldn’t help Grandma across the street. But we have no such reason.)
Can we use a similar response to handle tiny probabilities of vast utilities? Perhaps we can argue that giving $5 to AMF has at least as much chance of saving 10^10^10^10 lives as giving money to the Mugger. Generalizing, perhaps we can argue that past a certain point, the action profile of every action looks the same, even though it is funnel-shaped. Better yet, perhaps we can argue that action profiles which have better-looking “leftmost tips” will also be systematically better in the big, wide, funnel-shaped regions to the right. If either of these were true, then (with some plausible modifications to expected utility maximization enabling “cancelling out”) we could evaluate actions by summing the utility-probability products of each possible outcome in the leftmost tip, and ignoring everything further to the right. In practice this is what we do anyway, so this solution would be quite nice.
Ordinarily, we only consider the proximate effects of our actions and we only consider the most likely outcomes. The problem of cluelessness arises when we allow ourselves to consider distant effects, like the effect of our bodily motions on hurricanes decades from now. Importantly, it’s not that the probability of causing a hurricane by moving my arm is small. In fact it is quite large; there are excellent reasons to think that every motion we make has a big impact on dozens of weather events in the future, not to mention the genetic makeup of millions of people. With cluelessness, the outcomes we are thinking about are fairly likely; it’s just that (so the defense goes) they are equally likely on all the available actions and so they cancel out.
The problem of the Mugging arises when we allow ourselves to consider extremely unlikely outcomes. One way to think about the Mugging problem is as an objection to the standard defense against cluelessness: OK, so maybe helping Grandma and not helping Grandma are equally likely to cause hurricanes, but what about opening an interdimensional portal? Is each action equally likely to do that? OK, so what about pleasing the Utility Genie? Is each action equally likely to do that? The worry is that, while we may be able to answer “yes” to most of these questions, there are literally infinitely many such questions to consider, and we have no guarantee that the answer will be “yes” to all of them. And if it is not, we are in trouble. Of course, so long as we don’t consider those possibilities, we are fine—indeed, refusing to consider certain possibilities is an instance of solution category #1 from subsection 5.1. Similarly, for purposes of responding to Cluelessness it is enough that the probabilities almost cancel out. After all, hurricanes don’t do that much damage compared to some of the things we’ve considered thus far; if it turns out that the chance of causing a hurricane is a trillion trillionth larger if I help Granny across the street, so what? But this doesn’t work for the Mugging. If the probability of the Mugger telling the truth is 1/(10^10^10) and the probability of donating to AMF achieving the same result is 1/(10^10^10+1), you should overwhelmingly give to the Mugger over AMF. 10^10^10^10 lives saved is so many that if we multiply it by those two probabilities, the difference will be big enough to swamp other considerations (like the fact that AMF will also save a couple lives for sure). Summing up: Even if the action profiles mostly cancel out past a certain point, that’s not enough; they need to entirely cancel out. And I see no reason to think they will, and some reason to think they won’t.
Moreover, even if the funnels do cancel out past a certain point, it seems to me that the action profiles with the best-looking tips will not always have the best funnels. In other words, I think in practice, rather than vindicating our ordinary judgments, this method would lead to strange and unusual behavior. Here is one way this could happen even if we ignore outcomes of infinite utility:
For arbitrary unbounded computable utility functions, consider the class of hypotheses of the form “An A-loving genie sets the utility of the universe to X,” where A is the action you are considering doing, and X is a description of a finite number. The utility of these hypotheses will grow at the rate of the Busy Beaver function, i.e. faster than any computable function. So unless there is some more probable class of hypotheses that call your utility function, the long-run behavior of your action profiles will be dominated by hypotheses of this form. That in turn means that actions which genies are more likely to love are way better than other actions; your decision-making will be fanatical about pleasing hypothetical genies.
If we include outcomes of infinite utility, the situation becomes more straightforward: The best action in any given situation will be the one that has the highest probability of causing an infinite reward. I predict this will not vindicate ordinary judgments about what we should do, at least not those ordinary judgments made by non-religious people.
4: On rejecting expected utility maximization
This subsection considers the third main category of response to Pascal’s Mugging: rejecting expected utility maximization.
Arguably each of the responses considered in the previous subsections violates intuitively plausible principles about how our values and/or probabilities should be. Moreover, it seems that each response involves making arbitrary choices about (for example) which discount rate or cutoff to use. So, it’s reasonable to wonder if the best way to respond to the Mugging is to reject expected-utility maximization entirely. Perhaps the problem is not to do with the probabilities we use nor with the utilities we use but rather with the way we combine them. Instead of multiplying the probability by the utility, summing up, and picking the action with the highest total, we should…
There are many different ways to finish that sentence. This section will talk about two ways which seem to be a representative sample, as well as give some general considerations that apply to any response in this category.
The first way is to follow your heart, go with your gut, etc. Instead of using some sort of algorithm to analyze what you know about the situation (the possibilities, their probabilities, their utilities) and spit out an answer, you just think about it carefully and then do what seems right. This isn’t a terrible approach; it is what we do most of the time and it has worked all right so far. However, this approach has several problems. It is prone to biases of all sorts. It makes it very difficult for people to understand each other’s reasoning and converge to agreement. It is a black-box and therefore cannot be used to guide AI design or institutional choices.
The second way is to continue to use some sort of algorithm to analyze what you know and spit out an answer, but to make the algorithm more nuanced than expected utility maximization. For example, the philosopher Lara Buchak has a nice formalization and defense of a risk-weighted decision theory. (2013). The specific problem with her approach is that it violates the sure-thing principle, which many people find intuitively appealing. Also, it might be partition-dependent, meaning that which action is recommended by this approach depends on which way you choose to describe the problem. Note that it’s not enough to be risk-averse to solve the problem; you have to be very risk-averse, at least for extremely unlikely possibilities.
There are three additional problems that apply not only to these ways of responding to the Mugging but to any way that rejects expected utility maximization. The first is that expected utility maximization is, arguably, an optimal long-run policy, and similarly is optimal for large groups of people to follow. Assuming that the probabilities really are what you think they are, then in the long run (i.e. if enough independent versions of a given type of situation happen) there is an arbitrarily high probability that the average value of a gamble will be arbitrarily close to its expected utility. Of course, there are ways to resist this line of argument too.
Second, there are representation theorems which prove that so long as your preferences obey certain axioms, your behavior can be represented as resulting from expected-utility maximization using some utility and probability function. Thanks to the representation theorems, even if you say you are not maximizing expected utility, you are likely acting as if you are. Thus, you might say that you assign positive probability to every possibility and that you value each life saved equally and so forth, but the theorems show that either you are acting as if you don’t, or else that your preferences violate the axioms. It’s unclear how much of a problem this is, but it’s worth thinking about at least.
Finally, if your utility function is unbounded and your preferences are transitive (meaning that you don’t rank possible actions in a circle, ) you must be either reckless or timid. (Beckstead 2013) Recklessness means being always willing to trade a really high chance of an excellent outcome for an arbitrarily tiny chance of a sufficiently better outcome; it is similar to unboundedness for utility functions. Timidity means being sometimes unwilling to accept extremely small risks, even when accepting them vastly increases how good the positive possible outcomes are; it is similar to boundedness for utility functions. People who reject expected utility calculations will need to be either reckless, timid, or intransitive, and each of those options has difficulties. Since the difficulties are closely related to the difficulties for expected-utility maximizers that adopt one of the two strategies discussed previously, this undermines the Mugger-based rationale for rejecting expected utility maximization.
4.1: On the “Law of Large Numbers” defense of expected-utility maximization and its implications for long-termist projects
Section 6.1 compared the probability of success for projects like AI safety research with other, more ordinary behaviors like voting, buckling your seatbelt, and maintaining safety standards at nuclear plants. One idea worth exploring is that these ordinary behaviors are relevantly different from AI safety research, not because they are higher-probability-of-success, but because they can rely on the law of large numbers to help them out in a way that AI safety research cannot. Sure, any individual instance of seatbelt-buckling is negligibly likely to succeed, but collectively, there are so many instances of seatbelt-buckling in the world that many of them do succeed every day. Similarly, there are many nuclear plants, many voters, and many elections. By contrast, it’s not clear that we can say the same for AI safety research.
I think this is an idea worth developing. Here are some things to contend with: First, if the universe is infinite, such that everything that can happen does happen somewhere (e.g. if some sort of multiverse theory true) then every action will be able rely on the law of large numbers for backup. This might be taken as an interesting and acceptable consequence—what causes we should prioritize depends heavily on how big the world is!—but it could also be taken as a sign that we’ve gone wrong, since intuitively the size of the world shouldn’t make such a big difference to whether we should prioritize e.g. AMF or nuclear war prevention.
Second, there’s work to be done making this idea precise. What are the relevant categories for deciding whether the law of large numbers applies? Using the category “seatbelt-bucklings-by-Daniel-on-Christmas”, the law of large numbers does not apply. Using the category “decisions involving the increase or decrease of existential risk”, the law of large numbers comes to the rescue of AI safety research—after all, there are trillions of such decisions made over the course of human history, and collectively they determine the result just as in the case of voting.
5: Act-focused vs. World-focused graphs and the implications for long-termism
This article so far has measured outcomes relative to some sort of default point for your decision, perhaps what would happen if you do nothing: In the early diagrams, saving N lives has utility N, and doing something with no effect (like voting for an election and not making a difference) as having utility 0. But this is a potentially problematic way to do things; it leads to some inconsistencies between how individuals should behave and how groups should behave. Perhaps we should take a less self-centered perspective, and assign utility to outcomes simply on the basis of what the world contains in that outcome. (This is in fact standard in decision theory.)
So, for example, a lifeless world might get utility 0, a world like ours that has 10 people in it throughout history might get utility f(10) for some s-shaped utility function f, and a world almost exactly like that one except where you save a life might get utility f(1+10).
This is a more elegant way of defining utility functions, though it is in some ways less intuitive. Nick Beckstead has an extensive discussion of this sort of thing in his thesis (2013). World-focused utility functions have the interesting and arguably problematic implication that the value of what we do might depend significantly on what goes on in faraway and long-ago places. For example, if we assign diminishing returns to scale for happy human lives, then if we find out that an ancient human civilization arose a hundred thousand years ago and flourished for eighty thousand years before collapsing, we would downgrade our estimate of how important our altruistic work was.
How would it affect long-termism? Well, the basic situation would not change: Sufficiently low bounds on the utility function would make trouble for long-termist projects; sufficiently high bounds would vindicate them. Sufficiently strict cutoffs for which possibilities to consider would make trouble for long-termist projects; sufficiently inclusive sets of possibilities considered would vindicate them. I suspect, though, that this change would in some ways make it easier for long-termist projects to shelter within the herd. Intuitively there is a big difference between “Save one life for sure” and “Save 10 lives with probability 0.1.” But there is a much smaller difference, intuitively, between:
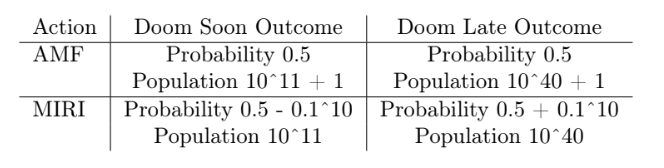
When described this way, the two options look basically the same. So I suspect that a procedure that treated them significantly differently would be harder to justify.
Bibliography
This section contains many of the things I read in the course of writing this article. I’ve organized them into categories to make it easier to browse around. At times I’ve added a short comment or summary as well.
Encyclopedias, wikis, etc.:
St. Petersburg Paradox (Wikipedia)
Academic literature:
Askell, Amanda. (2018) Pareto Principles in Infinite Ethics. 2018. PhD Thesis. Department of Philosophy, New York University.
–This thesis presents some compelling impossibility results regarding the comparability of many kinds of infinite world. It also draws some interesting implications for ethics more generally.
Beckstead, Nick. (2013) On the Overwhelming Importance of Shaping the Far Future. 2013. PhD Thesis. Department of Philosophy, Rutgers University.
Hájek, Alan. (2012) Is Strict Coherence Coherent? Dialectica 66 (3):411-424.
--This is Hajek's argument against regularity/open-mindedness, based on (among other things) the St. Petersburg paradox.
Hájek, Alan and Smithson, Michael. (2012) Rationality and indeterminate probabilities. Synthese (2012) 187:33–48 DOI 10.1007/s11229-011-0033-3
--The argument appears here also, in slightly different form.
Briggs, Rachel. (2016) Costs of abandoning the Sure-Thing Principle. Canadian Journal of Philosophy, Vol 45. No 5-6. 827-840.
–This pushes back against Lara Buchak’s project below.
Buchak, Lara. (2013) Risk and Rationality. Oxford University Press.
--This is one recent proposal and defense of risk-weighted decision theory; it's a rejection of classical expected utility maximization in favor of something similar but more flexible.
Colyvan, M. and Hajek, A. (2016). Making Ado Without Expectations. Mind, Vol. 125 . 499 . July 2016
--Explores and attacks two recent attempts to modify expected utility maximization: a useful companion to Buchak.
Bostrom, N. (2009). "Pascal's Mugging". Analysis 69 (3): 443-445.
--A simplified and streamlined explanation of the Mugging.
Bostrom, N. "Infinite Ethics." (2011) Analysis and Metaphysics, Vol. 10: pp. 9-59
--Discusses various ways to avoid "infinitarian paralysis," i.e. ways to handle outcomes of infinite value sensibly.
Easwaran, K. (2007) ‘Dominance-based decision theory’. Typescript.
--Tries to derive something like expected utility maximization from deeper principles of dominance and indifference.
Parfit, D. (1986) Reasons and Persons. Oxford University Press.
--A giant text full of interesting ideas, especially in personal identity and population ethics.
Lenman, D. (2000) “Consequentialism and Cluelessness.” Philosophy & Public Affairs. Volume 29, Issue 4, pages 342–370, October 2000
--An early paper on the cluelessness problem.
Greaves, H. (2016) “Cluelessness.” Proceedings of the Aristotelian Society 116 (3):311-339
--A recent paper on the cluelessness problem.
Smith, N. (2014) “Is Evaluative Compositionality a Requirement of Rationality?” Mind, Volume 123, Issue 490, 1 April 2014, Pages 457–502.
--Defends the “Ignore possibilities that are sufficiently low probability” solution. Also argues against the bounded utilities solution.
Sprenger, J. and Heesen, R. “The Bounded Strength of Weak Expectations” Mind, Volume 120, Issue 479, 1 July 2011, Pages 819–832.
--Defends the “Bound the utility function” solution.
Turchin, A. and Denkenberger, D. “Global Catastrophic and Existential Risks Communication Scale.” Futures. Accessed online at https://philpapers.org/rec/TURGCA
--Contains estimates of the probabilities of various catastrophes.
Ord T, Hillerbrand R, Sandberg A. (2010) Probing the improbable: methodological challenges for risks with low probabilities and high stakes. Journal Of Risk Research [serial online]. March 2010;13(2):191-205. Available from: Environment Complete, Ipswich, MA.
--Points out that when our estimates of the probability of something are very low, our upper bound on the probability might be significantly higher than our estimate, since our estimate may be wrong.
Existing informal debate focused on the application of the Mugging to cause prioritization:
https://www.vox.com/2015/8/10/9124145/effective-altruism-global-ai
--Important popular article using the Mugging argument against long-termism.
http://effective-altruism.com/ea/m4/a_response_to_matthews_on_ai_risk/
--A response to the above.
http://effective-altruism.com/ea/qw/saying_ai_safety_research_is_a_pascals_mugging/
--Another response.
http://slatestarcodex.com/2015/08/12/stop-adding-zeroes/
--Another response.
http://lesswrong.com/lw/h8m/being_halfrational_about_pascals_wager_is_even/
--Yudkowsky again, saying many different things in one post. Notably, he has a paragraph or two on Mugging vs. x-risk.
http://www.overcomingbias.com/tag/pascals-mugging
--Old short blog post by Rob Wiblin. Title says it all: "If elections aren't a Pascal's Mugging, existential risk shouldn't be either."
http://lesswrong.com/lw/z0/the_pascals_wager_fallacy_fallacy/
--Makes the point that the utilities being really high shouldn't hurt a prospect, even though if you don't think about it too much that makes it pattern-match more easily to the Mugging. The problematic aspect of the Mugging is the poor probability of success, not the high value of success.
https://blog.givewell.org/2014/06/10/sequence-thinking-vs-cluster-thinking/
--A useful reflection by GiveWell, now a classic. It grapples with a very similar problem to this one, and it outlines an important alternative to expected utility maximization. That said, it can be interpreted as a way to handle uncertainty and error in our models, rather than as a rejection of expected utility maximization.
https://www.givewell.org/modeling-extreme-model-uncertainty
--More of the same line of reasoning.
http://lesswrong.com/lw/745/why_we_cant_take_expected_value_estimates/
--Similar post by Karnofsky, but even more detailed.
https://www.lesswrong.com/posts/JyH7ezruQbC2iWcSg/bayesian-adjustment-does-not-defeat-existential-risk-charity
--A reply to the above.
Existing informal debate focused on the philosophical problem rather than the application to cause prioritization:
http://lesswrong.com/lw/633/st_petersburg_mugging_implies_you_have_bounded/
--Similar argument to what Hajek says: making use of St. Petersburg to mug us. Concludes that our utility function should be bounded, unlike Hayek who concluded that we should reject open-mindedness/regularity.
http://lesswrong.com/lw/ftk/pascals_mugging_for_bounded_utility_functions/
--An arguably problematic implication of bounded utility functions.
De Blanc, Peter. (2007) Convergence of Expected Utilities with Algorithmic Probability Distributions. On ArXiv: arXiv:0712.4318 [cs.AI] https://arxiv.org/abs/0712.4318
--A proof for something like the following: Unbounded utility functions that are perception-determined have funnel-shaped action profiles. Of course only some strange people have perception-determined utility functions (i.e. egoist hedonists).
http://lesswrong.com/lw/116/the_domain_of_your_utility_function/
--Argument by de Blanc that we shouldn't have perception-determined utility functions.
http://www.spaceandgames.com/?p=22
--In the comments people discuss how non-perception-determined utility functions can sometimes avoid the problem.
https://thezvi.wordpress.com/2017/12/16/pascals-muggle-pays/
--Some recent thoughts on the Mugging. Interprets status quo bias and scope insensitivity as nature's solution to the Mugging.
https://www.lesserwrong.com/posts/8FRzErffqEW9gDCCW/against-the-linear-utility-hypothesis-and-the-leverage#HsgwuSiQ4PEBy8JcG
--Contains great argument for bounded utility functions, also an OK argument against the leverage penalty. (I don't think it works but I think a different version of it would work.)
http://reducing-suffering.org/why-maximize-expected-value/
--Summary of some of the main reasons to maximize expected utility.
Miscellaneous:
http://rationallyspeakingpodcast.org/show/rs-190-amanda-askell-on-pascals-wager-and-other-low-risks-wi.html
--Great, engaging discussion of all of these ideas by Amanda Askell and Julia Galef
https://80000hours.org/problem-profiles/positively-shaping-artificial-intelligence
--80k profile on AI safety careers
Gelman, Silver, and Edlin: “What is the probability your vote will make a difference?” https://nber.org/papers/w15220
--Contains estimates for US presidential elections
https://nickbostrom.com/astronomical/waste.html
--Calculation of the population attainable if we don’t all die
https://www.linkedin.com/pulse/unexpectedly-high-expected-value-single-vote-victor-haghani
--Calculation of the expected value of voting
http://www.killerasteroids.org/impact.php
--Info about asteroid impacts
https://www.epa.gov/environmental-economics/mortality-risk-valuation#whatisvsl
--Explanation of how the EPA measures things like "the value of a statistical life."
http://effective-altruism.com/ea/1hq/how_you_can_save_expected_lives_for_020400_each/
--ALLFED, an effort to prepare the world to feed everybody in the event of a catastrophic agricultural shortfall
http://www.existential-risk.org/concept.html
--Introduction to existential risk prevention and argument that it should be a global priority
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5092084/
--Biohazard safety standards
http://lesswrong.com/lw/2ur/probability_and_politics/
--Blog post containing another calculation of the value of voting
This is the fifth and final post in a series. Here are the first, second, third, and fourth posts.
Notes:
43: Of course, a probability function by itself doesn’t lead to any sort of action profile; it needs to be combined with a utility function. In this section we’ll assume your utility function is linear in happy lives saved.
44: Few people (though I have met some!) claim to have perception-determined utility functions. A perception-determined utility function is one that evaluates the utility of a possibility entirely on the basis of what you perceive in that possibility. For example, it evaluates a possibility in which you have a successful career as equal to a corresponding possibility in which you have a very realistic hallucination of a successful career.
45: This is bad because standard accounts of updating on the basis of evidence (e.g. Bayesianism) make it impossible for the probability to rise above 0 once it reaches that point. Instead of getting closer to the truth when you find more evidence, you’ll end up doubting your senses!
46: Technically Solomonoff Induction does not say to be open-minded; it ignores all uncomputable hypotheses, for example. But it assigns positive probability to sufficiently many possibilities that it might as well be open-minded for our purposes.
47: I obtained this estimate by thinking about how many bits it takes to stream an HD movie for several days. This is probably a conservative estimate for a variety of reasons, e.g. our attention is limited and so we probably aren’t able to distinguish one pixel being a slightly different shade in an unimportant part of our visual field. If you think this is too generous, we could make it many orders of magnitude smaller and the argument would still work.
48: Note that the probability will actually be a bit less than this, depending on how unconfident you are that Boltzmann Brains really are possible as our current theories say they are. However, this factor is minor and can be ignored; even if you were 99.9999999% certain that mainstream science is wrong in this way, that would only change the result by a couple orders of magnitude.
49: A utility function that has diminishing returns to scale, but that nevertheless is unbounded, will still lead to problematic funnel-shaped action profiles. To see this, consider possibilities in which there are infinitely many happy lives saved. Or consider hypotheses of the form “And then a magic genie remakes the universe so that it has utility X.” So this section focuses on bounding the utility function rather than merely applying diminishing returns, though much of what it says applies equally to both strategies.
50: Technically it is useful to distinguish between being bounded above and being bounded below, but for our purposes this definition works fine.
51: Classic utilitarianism, prioritarianism, preference utilitarianism… the exception may be average utilitarianism, but that depends on precisely how it is cashed out. Longer happy lives and more sophisticated pleasures are two ways in which even an average utilitarian utility function could be unbounded. For more discussion, see Beckstead (2013).
52: Alternatively, if we are looking at the state of the world rather than the results of your action, utilitarianism would say that a happy life saved is just as valuable regardless of the population of the world. This distinction will be discussed more in the next section.
53: Assuming all lives being saved are equally happy.
54: It’s important to note that the friendship example and others like it can be explained away, e.g. “What you value is the enjoyment you get out of friendship, having someone to talk to, etc. and you already have those things once you have 1000 friends.” But we could also take it at face value, and think that our utility really is bounded. There are various arguments in the literature about this, e.g. https://en.wikipedia.org/wiki/Experience_machine.
55: One important criticism of bounded utilities, given by Hájek (2012) is that it isn’t the job of rationality to decide what utility function you should have. As far as I can tell this applies equally to non-regular probabilities though; it isn’t the job of practical rationality to decide what credences you should have, and the problem discussed in this article is a problem of practical rationality.
56: This is because our world is a chaotic system. Small perturbations at almost any point in the system end up causing large changes in the system after sufficient time has passed. “The butterfly effect” is an example of this. A more fleshed-out example: Different sperm contain different genes, and so if any given act of conception had taken place a minute earlier or a minute later, likely the resulting baby would have had different genes. Different genes lead to different personality and appearance which leads to other acts of sexual intercourse being delayed slightly (or more!) leading to more changes in the future population… etc. For this reason, it’s likely that a choice to help Grandma across the street will make a difference in the genes and personalities of a significant portion of the world population many generations later.. Since the behavior of nations often depends on the personalities of individual leaders, the geopolitical landscape will likely look dramatically different 500 years from now depending on whether you help Grandma or not! See Lenman (2000) for more on this issue.
57: See the discussion of genies below.
58: And if there is some more probable class of hypotheses that call your utility function, then those hypotheses will dominate the long-run behavior of your action profiles.
59: Scope insensitivity, status quo bias, availability heuristic… the list goes on. Most introductory EA material will cover this sort of thing.
60: The sure-thing principle, roughly, is that if two actions yield the same utility if event E obtains, and E is equally likely to obtain supposing you do each action, then your choice between those actions shouldn’t depend on what the utility or probability of E is. In other words, we should be able to simplify our decision-making by ignoring those possibilities that are the same across all our available actions--if rain will make you stay inside, rendering your decisions about what to pack irrelevant, then your decision about what to pack shouldn’t depend on what your indoor options are. For a deeper explanation of what’s going on here (and a defense of her view) read the original Buchak (2013).
61: I heard this from Richard Pettigrew (personal conversation).
62: Adding an extra penalty to unlikely outcomes can be thought of as equivalent to taking your funnel-shaped action profiles and squishing them down by penalizing the utility of low-probability outcomes, according to some penalizing function. For this to solve the problem, the penalty must be sufficiently severe; this is harder than it sounds.
63: For more on these arguments for expected-utility maximization, see https://plato.stanford.edu/entries/rationality-normative-utility/ and http://reducing-suffering.org/why-maximize-expected-value/.
64: Again see https://plato.stanford.edu/entries/rationality-normative-utility.
65: There are different representation theorems using different axioms. There isn’t enough space to explain the axioms here, but see https://plato.stanford.edu/entries/rationality-normative-utility/ Joyce (1999) for details.
This is the fifth and final post in a series. Here are the first, second, third, and fourth posts.
