Thanks to the members of the Global Priorities Reading Group at the Paris School of Economics, especially David Bernard, Christian Abele, Eric Teschke, Matthias Endres, Adrien Fabre, and Lennart Stern, for inspiring this post, and for giving me great feedback. Thanks too to Aaron Gertler for very helpful comments.
Brief Summary
Longtermists face a tradeoff: the stakes of our actions may be higher when looking further into the future, but predictability also declines when trying to affect the longer-run future. If predictability declines quickly enough, then long term effects might “wash out”, and the near term consequences of our actions might be the most important for determining what we ought to do. Here, I provide a formal framework for thinking about this tradeoff. I use a model in which a Bayesian altruist receives signals about the future value of a neartermist and a longtermist intervention. The noise of these signals increases as the altruist tries to predict further into the future. Choosing longtermist interventions is relatively less appealing when the noise of signals increases more quickly. And even if a longtermist intervention appears to have an effect that lasts infinitely long into the future, predictability may decline sufficiently quickly that the ex ante value of the longtermist intervention is finite (and therefore may be less than the neartermist intervention).
Intro
Longtermism is roughly the claim that what we ought to do is mostly determined by how our actions affect the very long-run future. The intuition that underlies this claim is that the future might be very long and very big, meaning that the vast majority of value is likely to be realised over the long-run future. On the other hand, the predictability of the effects of our actions is likely to decrease as we extend our time-horizon to the very long-run future. For example, it may be impossible to have a predictable and significant effect on the state of the world more than 1,000 years from now.
Altruists thus face a trade-off: if we attempt to improve the future over the long run rather than in the near term, there may be higher stakes, but less predictability. If the predictability of the effects of our actions declines quickly enough to counteract the increased stakes, then near term effects will dominate our ex ante moral decision-making, contrary to the claims of the longtermist. This objection to longtermism has been called the “washing out hypothesis” and the “epistemic challenge to longtermism”, and you can find further discussions of it in the links. It is seen as one of the most important and plausible objections to the claims of the longtermist.
In this post, I aim to provide a simple mathematical framework for thinking about the washing out hypothesis that formalises the tradeoff between stakes and predictability.
Model summary
The basic idea behind the model is as follows:
- An altruist tries to determine the best intervention by carrying out cost-effectiveness calculations. We assume that these exercises will yield an unbiased but noisy signal of the value of an intervention at every time t in the future.
- In order to account for the fact that predictability decreases as we extend the time horizon, we assume that the noise on these cost-effectiveness signals will increase as the altruist looks further into the future. Using a Bayesian framework, we can show that this gives the altruist an as-if discounting function, where the altruist acts “as if” the future matters less. The altruist has perfectly patient preferences, so they do not discount the future because they “care” about the future less (see Hilary Greaves’ discussion for why we might think this is ethically inappropriate). Rather, they discount the future because it is empirically more difficult to predict.
- To capture the intuition that the stakes on longtermist actions may be higher, we assume that the altruist is choosing between two alternative interventions, a neartermist intervention (N) and a longtermist intervention (L). The cost-effectiveness signals suggest that N will only have an effect that lasts a short time, while the L will have an effect that doesn’t start immediately but that lasts for a very long time.
The framework is pretty general, but it might be useful to have examples in mind. Imagine that N is an intervention that distributes cash transfers to poor individuals: this leads to large predicted benefits for recipients in the near term, but no predicted effect in the long term. And L might be an intervention that reduces carbon dioxide emissions. The cost-effectiveness exercise predicts 0 benefits in the near term for this intervention, but by reducing the risk of catastrophic climate change it is predicted to lead to a stream of increased value in the future. In this example, and in the framework more generally, we are assuming that the stakes of longtermist actions are larger because the future is very long (and mostly ignoring the fact that the future may also be very big).
The model describes the conditions under which an altruist should choose the longtermist intervention over and above the neartermist intervention, given that the effects of the longtermist interventions may be larger in scale but less predictable. One of the key determinants of the optimal choice is the shape of the forecasting error function, which describes how quickly the future becomes unpredictable as we try to predict further and further into the future. The longtermist intervention is less appealing (relative to the neartermist intervention) in cases when the future more rapidly becomes less predictable as we extend our prediction horizon. And we can also show that if the longtermist intervention is predicted to have effects that last infinitely long, this does not entail that L will always be preferable to N. If predictability falls fast enough (specifically, more than linearly), then the value of L will not tend towards infinity even as our time horizon extends towards infinity.
Hopefully, the model will be able to act as a useful thinking tool for examining the ideas of longtermism and the washing out hypothesis in a slightly more formal way. One important takeaway appears to be the importance of the shape of the forecasting error function. The shape of is essentially an empirical question. Thus, a key message of this framework is that we need to do more empirical research on the forecasting error function, including aspects such as (i) how quickly forecasting noise increases with prediction time-horizon, (ii) under what conditions does forecasting noise not increase rapidly with time-horizon, and (iii) how can we better predict the long-run effects of actions today.
(A note on precedents: The framework I develop below is similar in spirit and aim to Christian Tarsney’s great work on the epistemic challenge to longtermism, although the model structure is rather different (my framework is essentially a Bayesian one; Christian models the loss of predictability using “exogenous nullifying events”). The idea was very much inspired by Holden Karnofsky’s discussions on the interpretation of cost-effectiveness estimates. The model itself is an extension of the framework seen in Gabaix & Laibson 2017, although the application I explore here is very different to the original paper.)
Model
Model setup
In the model, an altruist with perfectly patient preferences chooses between a neartermist intervention (N) and a longtermist intervention (L). The moment at which they choose is . For simplicity, assume that N and L have the same cost, so that differences in benefits will correspond with differences in cost-effectiveness.
Preferences: the altruist has an objective function that is total utilitarian with no pure time discounting (they are perfectly patient), so that the overall value of choosing an intervention is given by:
where u(t) is the true benefit of the intervention at time t.
Cost-effectiveness estimates: the altruist carries out cost-effectiveness estimates by researching the effects of each intervention. We assume that this exercise yields an unbiased but noisy signal of the true benefit for every time period in the future. So for every t greater than 0, the altruist observes:
where is the signal for the value, composed of the true value of the intervention and some noise .
To account for the idea that the predictability of the effects of the altruist’s actions decreases when increasing the time horizon, we assume that the noise on the signal increases with time-horizon, that is:
where is the forecasting error function. This function describes how the variance of the noise increases as the altruist tries to predict further into the future. Intuitively, since far-future effects are harder to predict than near-future effects, the cost-effectiveness estimates will become less reliable as the time-horizon increases. We will postulate different functional forms for below.
To make the model tractable, we assume that the altruist’s prior beliefs over and are normally distributed. And suppose that the mean of the prior value on any action is 0. Roughly, this amounts to the assumption that (absent other information) we expect that our actions will have neither a net positive nor net negative effect on the world. So the priors are:
Under these assumptions, we can write the altruist’s posterior expectation for the value of an intervention at time using an “as-if discounting function” D(t) (see Gabaix & Laibson 2017):
When the altruist observes a signal , they need to take account of the fact that the signal not only reflects the true value of the intervention , but also some noise due to prediction error . When most of the variance of the signal comes from the true value (the signal is not noisy) then will be low, and will be close to 1. In this case, the posterior expected value of the intervention at will be close to ; the altruist can take the signal “at face value”. On the other hand, when examining the effects on the long run future, the prediction error on any forecasts will be larger, meaning that the signal is noisier and thus constitutes weaker evidence for the true value of the intervention. Since more of the variance of the signal is due to prediction error, so , and will tend towards 0, because the altruist has to discount their posterior towards their prior (which is in this case 0). Broadly this captures the intuition that when calculating a posterior belief for the value of an intervention, the signal of the value of an intervention should be discounted to account for the fact that the future is unpredictable.
To model the differences between neartermist and longtermist interventions, I suppose a particular structure on the signals that are generated by the cost-effectiveness estimates. For the neartermist intervention, the signal received from the cost-effectiveness indicates that the value will be:
In other words, according to the cost estimate, the value of the intervention will be high immediately (at ) and last a short time until , and then drop to 0.
The longtermist intervention has a different structure - the cost-effectiveness estimate indicates that it won’t start generating benefits until some time . The predicted benefits are different at any given time compared to the N intervention (in the example below, I assume , but this isn’t essential for any of the results). But the benefits of L last a long time (until ).
(In principle, it would be possible to imagine many other types of signal structures that could be generated, depending on the exact type of intervention. It would be interesting to explore what other signal structures might model “real-world” proposals for longtermist interventions.)
Here’s a simple diagram of what the signals for each intervention might look like. We’re imagining that a cost-effectiveness exercise on a bed-net intervention tells us that “this intervention will yield benefits of 100 QALYs each year, realised over the next 70 years; then, once the beneficiaries of the programme have passed away, there will be no benefits of the intervention”. But the longtermist intervention doesn’t yield any predicted benefits until year 200, and then provides a smaller stream of value (50 QALYS at each year) for a much longer period (until year 1000).
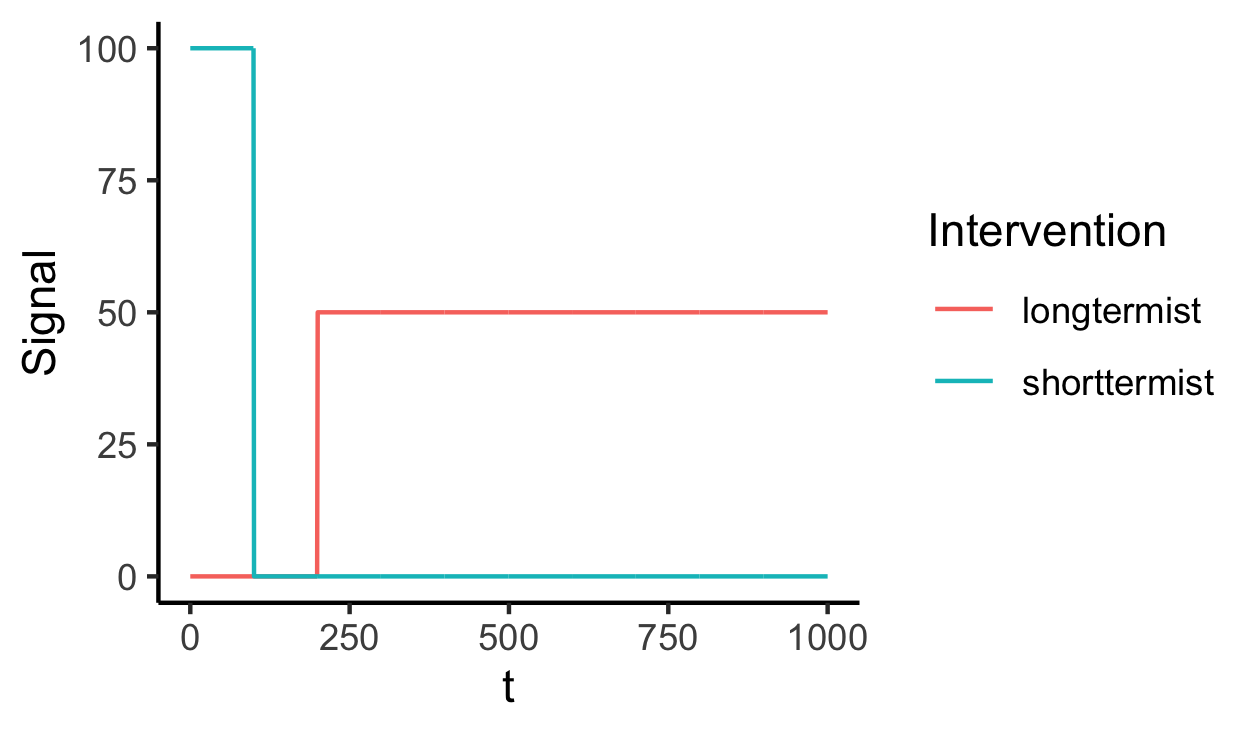
Now that we have defined the signals received by the altruist for each intervention, we can calculate the total posterior expected value for each intervention using the as-if discounting function and by integrating over all of time:
The total posterior expected value for the neartermist intervention is:
And for the longtermist intervention it’s:
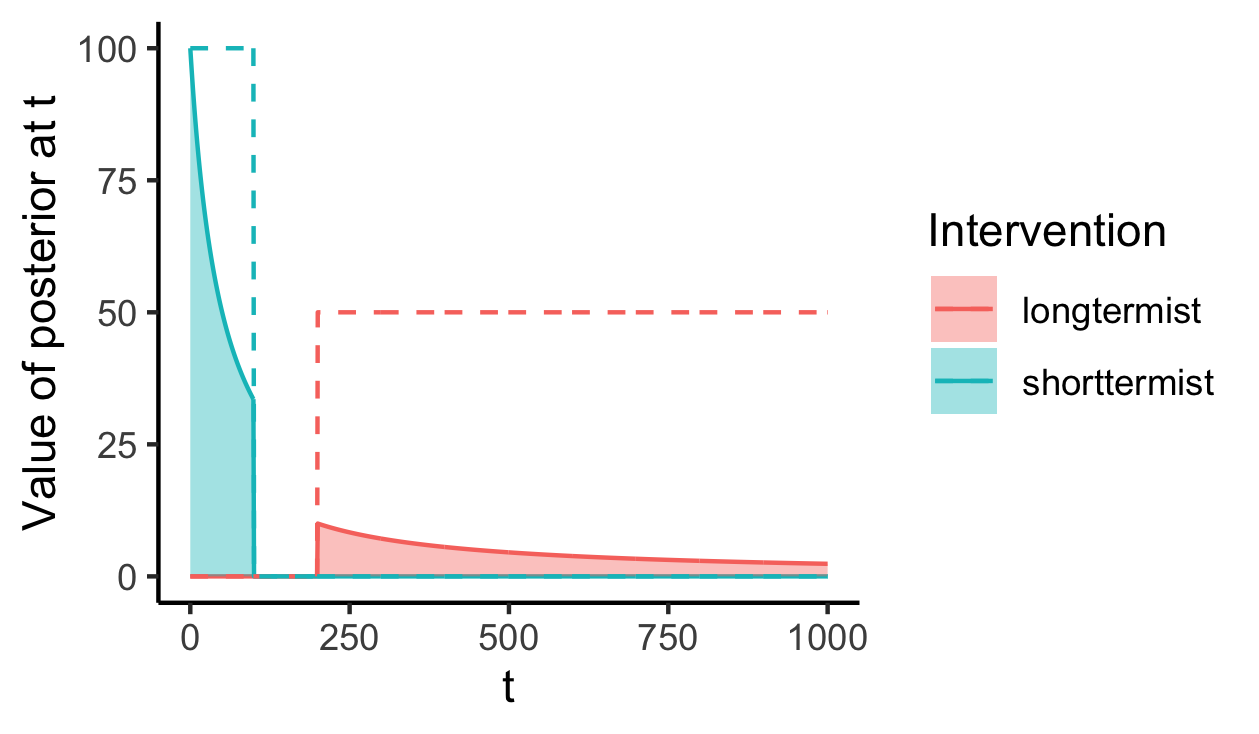
The diagram below gives a visual intuition for these expressions. The dotted lines represent the signals (the same as the previous diagram). The solid lines are the posterior expected value for each intervention at each t, which are calculated by discounting the signals to account for reductions in predictability as t increases. Then, the total posterior expected value of each intervention is given by the shaded area under the curves. We can see that because the longtermist intervention starts later than the neartermist intervention, it is “discounted” more heavily. This captures the simple intuition that the reduction in predictability from the future will “hurt” the value of the longtermist interventions more than the neartermist ones.
Model results
Linear case
We can find the solution to the integrals that describe the total posterior value of each intervention if we specify the shape of the forecasting error function . One simple case is where:
i.e. the forecasting noise increases linearly as the time horizon increases. Here, is a parameter that describes how quickly things become unpredictable as we extend our time horizon. In this case, the as-if discounting function becomes a hyperbolic function of time:
How do the different parameters affect the desirability of choosing the longtermist intervention over and above the neartermist intervention? To see this, we can derive an expression for the (posterior) relative value of choosing the longtermist intervention compared to the neartermist:
where (see proof here). The altruist should choose the longtermist intervention when RV > 1, and choose the neartermist intervention when RV < 1.
Intuitively, the posterior relative value of the longtermist intervention is higher when:
- The longtermist intervention lasts longer (when is higher)
- The longtermist intervention starts earlier (when is lower)
- The neartermist intervention is shorter (when is lower)
- When the relative size of the value-signal from the longtermist intervention is higher ( is higher)
We can also show that RV is decreasing in (see proof). This captures one of the key features of the washing out hypothesis. When is higher, the future becomes less predictable more rapidly as we extend our time horizon further, meaning that longtermist interventions are less appealing compared to near termist interventions. This insight points us towards an important aspect of empirical research. In particular, we need to know more about how quickly our ability to predict the effects of our actions declines as we extend our time horizon.
Behaviour when longtermist intervention appears to have benefits that last infinitely long
Another interesting insight from the model comes when we consider the behaviour when tends to infinity. We might think that as long as is high enough, the longtermist intervention should always be preferable to the neartermist intervention. If our cost-effectiveness estimates suggest that the longtermist intervention yields benefit for almost infinitely long, it might feel plausible that this will always be enough to outweigh the short-term benefits of a neartermist intervention. In fact, however, we can show that if the prediction error increases at an increasing rate, then predictability will decline quickly enough to “cancel out” the longer time horizon. Very long time horizons are not always sufficient to guarantee that the longtermist intervention is the best choice.
To examine this intuition, let’s now suppose that the forecasting error function can now be non-linear, described by:
Before, we had , corresponding to a linear forecasting error function. Now, if , forecasting noise will increase at an increasing rate as the time horizon extends out to the future. If , forecasting noise will increase but at a slower and slower rate as the time-horizon increases.
What happens to the posterior value of the longtermist intervention when the intervention appears to yield benefits infinitely far into the future? The expression for the value is:
And it can be shown that:
- When ,
- But when , we can bound where the upper bound is
So when the forecasting error function increases less-than-linearly, having an infinite time horizon means that we always favour a longtermist intervention relative to a neartermist one. On the other hand, with a forecasting error function that increases at an increasing rate, then this may not be sufficient to generate very high expected values for the long-termist intervention even if our time horizon is effectively infinite.
One intuitive way of thinking of this result is as a “race” between two competing factors as the time horizon increases. On the one hand, the stakes increase because value is realised for a longer duration. But on the other hand, the predictability of one’s actions decreases, meaning that extra value is discounted more. When , the loss of predictability is more than linear and it wins the “race”, meaning that total posterior value is bounded and doesn't continue towards infinity. On the other hand, when , the increase in value due to increased stakes always outweighs the loss in predictability as increases, so total value keeps increasing towards infinity as the horizon stretches towards infinity.
Broadly, this result indicates that the shape of the relationship between time and forecasting error may be crucial in determining the relative value of longtermist vs neartermist interventions when our time horizon gets very large.
Discussion
Both the linear and the non-linear version of the model point towards the crucial importance of the shape of the forecasting error function. In the linear case, we showed that the relative value of the longtermist intervention was decreasing in the value of . When the future becomes less predictable more quickly as the forecasting time horizon increases, longtermist interventions are less appealing on the margin. After allowing for non-linear forecasting error functions, we find that the parameter (that describes whether increases at a decreasing, constant, or increasing rate) is the key determinant of whether a longtermist intervention will always dominate in expected-value terms when our time horizon is effectively infinite.
It’s worth restating that the shape of the forecasting error function is an empirical question. The model’s results therefore underscore the need for more empirical research in trying to understand how forecasting accuracy declines as we increase the time horizon of forecasts, as this may have a direct bearing on the relative merits of longtermist interventions. If you are interested in this area, see initial work on this by David Bernard e.g. here and here. Note that the type of forecasting required here is not just state forecasting (predicting what will happen), but counterfactual forecasting (predicting what would happen if an intervention is carried out). While a fair amount of research has been carried out on state forecasting, counterfactual forecasting is much less well understood. And it may be a whole lot more tricky to do.
It’s worth pointing out that the model I’ve outlined above is extremely simplified, and so may fail to capture a number of features of the choice between interventions that may be important in real life. It would be worth exploring the effect of relaxing some of the simplifying assumptions I made, in order to see how robust the insights and conclusions of the model are. For example, I assumed (for the sake of tractability) that the value of the interventions was normally distributed. Most discussions in this area indicate that the distribution of the value/cost-effectiveness of interventions may be highly right skewed, so it would be interesting to explore the robustness of conclusions when using e.g. a log-normal distribution instead. Other aspects worth examining further include (i) the assumption of 0 priors for both types of intervention, (ii) the assumption that the signal received about the future value of interventions takes the same value at all time horizons ( are constant), and (iii) different shapes for the forecasting error function.
Another weakness of the model is that it doesn’t seem particularly appropriate for modelling some types of longtermist interventions. In particular, it’s not ideal for capturing the dynamics of interventions that aim to push the world into “attractor states” (states of the world such that once the world enters that state, it tends to stay in that state for an extremely long time). Since these are possibly the best candidates for interventions that manage to avoid the “washing out” trap, it would be useful to explore other models to understand these interventions in more depth.

It's worth noting that Tarsney's The epistemic challenge to longtermism, which you mention, deals explicitly with attractor states, and so I think better captures this stronger case for longtermism.
I agree! I think you're pointing towards a useful way of carving up this landscape. My framework is good for modelling "ordinary" actions that don't involve attractor states, where actions are more likely to wash out and longtermism becomes harder to defend (but may still win out over neartermist interventions under the right conditions). Then, Tarsney's framework is a useful way of thinking about attractor states, where the case for longtermism becomes stronger but is still not a given.
I'm unsure how many proposed longtermist interventions don't rely on the concept of attractor states. For example, in Greaves and MacAskill's The Case for Strong Longtermism, they class mitigating (fairly extreme) climate change as an intervention that steers away from a "non-extinction" attractor state:
Perhaps Nick Beckstead's work deviates from the concept of attractor states? I haven't looked at his work very closely so am not too sure. Do you feel that "ordinary" (non-attractor state) longtermist interventions are commonly put forward in the longtermist community?
The only intervention in Greaves and MacAskill's paper that doesn't rely on an attractor state is "speeding up progress":
I'd be interested to hear your thoughts on what you think the forecasting error function would be in this case. My (very immediate and perhaps incorrect) thought is that speeding up progress doesn't fall prey to a noisier signal over time. Instead I'm thinking it would be constant noisiness, although I'm struggling to articulate why. I guess it's something along the lines of "progress is predictable, and we're just bringing it forward in time which makes it no less predictable".
Overall thanks for writing this post, I found it interesting!
My intuition is that there'd be increasing noisiness over time (in line with dwebb's model). I can think of several reasons why this might be the case. (But I wrote this comment quickly, so I have low confidence that what I'm saying makes sense or is explained clearly.)
1) The noisiness could increase because of a speeding-up-progress-related version of the "exogenous nullifying events" described in Tarsney's paper. (Tarsney's version focused on nullifying existential catastrophes or their prevention.) To copy and then adapt Tarsney's descriptions to this situation, we could say:
As Tarsney writes:
2) The noisiness could also increase because, the further we go into the future, the less we know about what's happening, and so the more likely it is that speeding up progress (or making any other change) would actually have bad effects.
Analogously, I feel fairly confident that me making myself a sandwich won't cause major negative ripple effects within 2 minutes, but not within 1000 years.
Yeah this all makes sense, thanks.
As mentioned in another comment, my impression is that, in line with this, the most commonly proposed longtermist priority other than changing the likelihood of various attractor states is speeding up progress. Last year, I drafted a post that touched on this and related issues, and I really really plan to finally publish it soon (it's sat around un-edited for a long time), but here's the most relevant section in the meantime, in case it's of interest to people:
---
Beckstead writes that our actions might, instead of or in addition to “slightly or significantly alter[ing] the world's development trajectory”, speed up development:
Technically, I think that increases in the pace of development are trajectory changes. At the least, they would change the steepness of one part of the curve. We can illustrate this with the following graph, where actions aimed at speeding up development would be intended to increase the likelihood of the green trajectory relative to the navy one:
This seems to be the sort of picture Benjamin Todd has in mind when he writes:
However, I think speeding up development could also affect “where we end up”, for two reasons.
Firstly, if it makes us spread to the stars earlier and faster, this may increase the amount of resources we can ultimately use. We can illustrate this with the following graph, where again actions aimed at speeding up development would be intended to increase the likelihood of the green trajectory relative to the navy one:
Secondly, more generally, speeding up development could affect which trajectory we’re likely to take. For example, faster economic growth might decrease existential risk by reducing international tensions, or increase it by allowing us less time to prepare for and adjust to each new risky technology. Arguably, this might be best thought of as a way in which speeding up development could, as a side effect, affect other types of trajectory change.
---
(The draft post was meant to be just "A typology of strategies for influencing the future", rather than an argument for one strategy over another, so I just tried to clarify possibilities and lay out possible arguments. If I was instead explaining my own views, I'd give more space to arguments along the lines of Benjamin Todd's.)
Thanks for this Michael, I'd be very interested to read this post when you publish it. Especially as my career has taken a (potentially temporary) turn in the general direction of speeding up progress, rather than towards safety. I still feel that Ben Todd and co are probably right, but I want to read more.
Also, relevant part from Greaves and MacAskill's paper:
I think this is a very good point, and it's helping shape my ideas on this topic, thank you!
I guess it's true that most/all candidates for longtermist interventions that I've seen are based on attractor states. At the same time, it's useful to think about whether we might be missing any potential longtermist interventions by focusing on these attractor state cases. One such example that plausibly might fit into this category is an intervention that broadly improves institutional decision-making. Perhaps here, interventions plausibly have a long run positive impact on future value but we are worried that this will be "washed out" by other factors. It's not clear that there's an obvious attractor state involved. (Note that I'm not very confident in this; I could easily be persuaded otherwise. Maybe people advocate for improving institutional decision-making on the basis that it reduces the risk of many different bad attractor states.)
Thinking about this type of intervention, the results of my model can be read either pessimistically or optimistically from the longtermist's perspective (depending on your beliefs about the nature of the parameters):
I hadn't seen this post before, but to me it sounds like Beckstead's arguments are very much in line with the idea of attractor states, rather than deviating from it. A path-dependent trajectory change is roughly the same as moving from one attractor state to another, if I've understood correctly.
The argument he is making is that extinction / existential risks are not the only form of attractor state, which I agree with.
Whoops, yeah, having just re-skimmed the post, I now think that your comment is a more accurate portrayal of Beckstead’s post than mine was. Here’s a key quote from that post:
I haven't read that post but will definitely have a look, thanks.
I'd also be interested in dwebb's thoughts on this.
I'll share my own reactions in a few comment replies.
I think it's true that both Greaves and MacAskill and other longtermists mostly focus on attractor states (and even more specifically on existential catastrophes), and that the second leading contender is something like "speeding up progress".
I think this is an important enough point that it would've been better if dwebb's final paragraph had instead been right near the start. It seems to me like that caveat is key to understanding how the rest of the post connects to other arguments for, against, and within longtermism. (But as I noted elsewhere, I still think this post is useful!)
Thanks very much for writing this it. I'd started to wonder about the same idea but this is a much better and clearer analysis than I could have done! A few questions as I try to get my head around this.
Could you say more about why the predictability trends towards zero? It's intuitive that it does, but I'm not sure I can explain that intuition. Something like: we should have a uniform prior over the actual value of the action at very distant periods of time, right? An alternative assumption would be that the action has a continuous stream of benefits in perpetuity. I'm not sure how reasonable that is. Or is it the inclusion of counterfactuals, i.e. if that you didn't do that good thing, someone else would be right behind you anyway?
Regarding 'attractor states', is the thought then that we shouldn't have a uniform prior regarding what happens to those in the long run?
I'm wondering if the same analysis can be applied to actions as to the 'business as usual' trajectory of the future, i.e. where we don't intervene. Many people seem to think it's clear that the future, if it happens, will be good, and that we shouldn't discount it to/towards zero.
Thanks for some thought provoking questions!
The posterior estimate of value trends towards zero because we assumed that the prior distribution of u_t has a mean of 0. Intuitively, absent any other evidence, we believe a priori that our actions will have a net effect of 0 on the world (at any time in the future). (For example, I might think that my action of drinking some water will have 0 effect on the future unless I see evidence to the contrary. There's a bit of discussion of why you might have this kind of "sceptical" prior in Holden Karnofsky's blog posts.) Then, because our signal becomes very noisy as we predict further into the future, we weight the signal less and so discount our posterior towards 0. It would be perfectly possible to include non-zero-mean priors into the model, but it's hard for me to think (off the top of my head) in what scenarios this would make sense. In your example of having a continuous stream of benefits in perpetuity, it seems more natural to model this as evidence you've received about the effects of an intervention, rather than your prior belief about the effects of an intervention.
For attractor states, I basically don't think that the assumption of a signal with increasing variance as the time horizon increases is a good way of modelling these. That's because in some sense predictability increases over time with attractor states (at the beginning, you don't know which state you'll be in, so predictability of future value is low; once you're in the attractor state, you persist in that state for a long time so predictability is high). As MichaelStJules mentioned, Christian Tarsney's paper is a better starting point for thinking about these attractor states.
Thanks for writing this up! It's great to formalize intuitions, and this had a bunch of links I'm interested in following up on.
One simplifying assumption that got made was that both interventions cash out in constant amounts of utility for the duration of their relevance. You spoke at the end about the ways in which conclusions would change by changing assumptions; this seems like an important one! If utility increases over time, you have additional juice in that part of the race.
Is this basically addressed by you saying you weren't assuming the bigness of the universe (since if there's more people, presumably some good intervention will have more impact) + leaving aside attractor states? I think not quite, since attractor states mostly seem good by limiting the unpredictability rather than by increasing the impact, and I can imagine ways besides there being more people that a good intervention will increase in utility generation over time (snowball effects, allowing other good things to happen on top, etc).
But maybe it just doesn't add a lot to the central idea? The question is simply one of comparing integrals, and we can construct more complicated integrands and model a bunch of different possibilities / hopefully test them empirically and that will tell us a lot about how to proceed.
Thanks for this, and would love your thoughts!
You're right that the constant predicted benefits for each intervention is an important simplifying assumption. However, as you mention, it would be relatively easy to change the integrand to allow for different shapes of signalled benefits. For example, a signal that suggests increasing benefits as we increase the time horizon might increase the relative value of the longtermist intervention.
It quickly becomes an empirical question what the predicted-benefit function looks like, and so it will depend on the exact intervention we are looking at, along with various other empirical predictions. An important one is indeed whether we think the "size"/"scale" of the future will be much larger in value terms (e.g. if the number of individuals increases continuously in the future, the predicted benefits of L could plausibly increase over time).
About attractor states, you say:
I think that's basically true, although we need to be careful here about what we mean by "impact". Even if the "impact" at any one time of being in a good attractor state vs a bad attractor state may be relatively small, the overall "impact" of getting into that attractor state may be large because it persists for so long.
I sort-of agree, and I'm definitely quite supportive of research into all of those things. But I think "essentially an empirical question" might be a bit misleading, since it gets very hard to gather extremely relevant empirical data as the forecasting time horizon we're interested in gets longer.
My impression is that we currently have a tiny bit of fairly good data on 20 year forecasts of the most relevant kind. (I say "most relevant kind" to capture things like the forecasters making it clear what they were forecasting and seeming to be really trying to be accurate. In contrast, things like Nostradamus's predictions wouldn't count. See this great post for more explanation of what I mean here.)
Getting good data on 100 year forecasts of the most relevant kind will of course require waiting at least ~80 years. And so on for longer ranges.
So I think that, whatever empirical research we do, for the next few decades our views about the shape of f(t) over long time horizons will still have to be based on quite a bit of theory-, intuition-, or model-driven extrapolation from the empirical research.
That said, again, I am very much supportive of that empirical research, for reasons including that:
Yes, it appears that for long time horizons (>> 1000 years) there is no hope without theoretical arguments? So an important question (that longermism sort of has to address?) is what f(t) you should plug in in such cases when you have neither empirical evidence nor any developed theory.
But, as you write, for shorter horizons empirical approaches could be invaluable!
Thanks for the nice analysis.
I somehow have this (vague) intuition that in the very long time limit f(t) has to blow up exponentially and that this is a major problem for longetermism. This is sort of motivated by thinking about a branching tree of possible states of the world. Is this something people are thinking or have written about?
I haven't seen anything along these lines, but it would certainly be interesting if there were theoretical reasons to think that prediction variance should increase exponentially.
Ultimately though I do think this is an empirical question - something I'm hoping to work on in the future. One new relevant piece of empirical work is Tetlock's long-run forecasting results that came out last year: https://onlinelibrary.wiley.com/doi/abs/10.1002/ffo2.157
I just want to highlight that I think that counterfactual forecasting and its distinction from state forecasting are important and under-discussed topics (I'm grateful to Dave Rhys Bernard for making it salient to me in the past), even outside the context of the washing out hypothesis, long-range forecasting, or longtermism. So it's nice to see you highlight this here :)
Should that say "RV is decreasing in α "?
Yes indeed, kudos to Dave Bernard - he pointed out this distinction to me as well.
And good spot - sorry for the confusing error! I've now edited this in the text.
Do you have any plans to follow this up with versions of the model that relax/change some assumptions, or that try to capture things like attractor states or the future likely being far "larger" (i.e., containing more sentient beings, at least in the absence of an extinction event)?
Of course, Tarsney's paper already provides nice models for interventions focused on reaching/avoiding attractor states. But I wonder if it could be fruitful to see how the model structure here could be adapted to account for such interventions, and see if this generates different implications or intuitions than Tarsney's model does.
Somewhat relatedly, do you know what the results would be if we model noise as increasing sublinearly (rather than linearly or superlinearly), in a situation where the signal isn't suggesting the longtermist intervention has benefits for an infinite length of time?
Obviously this would increase the relative value of the longtermist intervention compared to the neartermist one, but I wonder if there are other implications as well, if the difference that that would make would be huge or moderate or small, what that depends on, etc.
One reason this seems interesting to me is that I'd currently guess that noise does indeed increase sublinearly. This is based on two things:
If GJP had involved questions with substantially longer time horizons, how quickly would superforecaster accuracy declined with longer time horizons? We can’t know, but an extrapolation of the results above is at least compatible with an answer of “fairly slowly.”"
Nice post, thanks! This seems like a useful model for guiding one's thinking. I'd like to especially compliment you on the diagrams - I think they helped me both understand and "have a feel for" what you were saying, plus they injected a nice bit of colour in :)
Thanks so much for the very insightful commentary! My thoughts are still evolving on these topics so I will digest some of your remarks and reply on each one.