Optimizer's curse

The optimizer's curse is the phenomenon that causes an agent optimizing over a set set of options with uncertain value to systematically overestimate the value of the chosen option.

Illustration

The authors of the paper that originally introduced the optimizer's curse provide a simple illustration of the phenomenon:^[1]

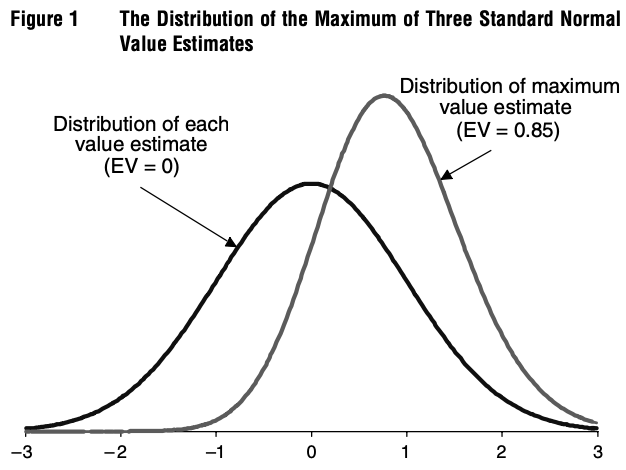
suppose that we evaluate three alternatives that all have true values ${\mu }_i$ of exactly zero. The value of each alternative is estimated and the estimates $V_i$ are independent and normally distributed with mean equal to the true value of zero (they are conditionally unbiased) and a standard deviation of one. Selecting the highest value estimate then amounts to selecting the maximum of three draws from a standard normal distribution. The distribution of this maximal value estimate is easily determined by simulation or using results from order statistics and is displayed in Figure 1. The mean of this distribution is 0.85, so in this case, the expected disappointment,$E[V_{i\ast }-{\mu }_{i\ast }]$, is 0.85.