Note: This post is adapted from a GPI working paper. We like hearing what you think about our work, and we hope that you like hearing from us too!

1 Introduction

Many EAs endorse two claims about existential risk. First, existential risk is currently high:

(Existential Risk Pessimism) Per-century existential risk is very high.

For example, Toby Ord (2020) puts the risk of existential catastrophe by 2100 at 1/6, and participants at the Oxford Global Catastrophic Risk Conference in 2008 estimated a median 19% chance of human extinction by 2100 (Sandberg and Bostrom 2008). Let’s ballpark Pessimism using a 20% estimate of per-century risk.

Second, many EAs think that it is very important to mitigate existential risk:

(Astronomical Value Thesis) Efforts to mitigate existential risk have astronomically high expected value.

You might think that Existential Risk Pessimism supports the Astronomical Value Thesis. After all, it is usually more important to mitigate large risks than to mitigate small risks.

In this post, I extend a series of models due to Toby Ord and Tom Adamczewski to do five things:

1. I show that across a range of assumptions, Existential Risk Pessimism tends to hamper, not support the Astronomical Value Thesis.
2. I argue that the most plausible way to combine Existential Risk Pessimism with the Astronomical Value Thesis is through the Time of Perils Hypothesis.
3. I clarify two features that the Time of Perils Hypothesis must have if it is going to vindicate the Astronomical Value Thesis.
4. I suggest that arguments for the Time of Perils Hypothesis which do not appeal to AI are not strong enough to ground the relevant kind of Time of Perils Hypothesis.
5. I draw implications for existential risk mitigation as a cause area.

Proofs are in the appendix if that’s your jam.

2 The Simple Model

Let’s start with a Simple Model of existential risk mitigation due to Toby Ord and Tom Adamczewski. On this model, it will turn out that Existential Risk Pessimism has no bearing on the Astronomical Value Thesis, and also that the Astronomical Value Thesis is false.

Many of the assumptions made by this model are patently untrue. The question I ask in the rest of the post will be which assumptions a Pessimist should challenge in order to bear out the Astronomical Value Thesis. We will see that recovering the Astronomical Value Thesis by changing model assumptions is harder than it appears.

The Simple Model makes three assumptions.

1. Constant value: Each century of human existence has some constant value $v$.
2. Constant risk: Humans face a constant level of per-century existential risk $r$.
3. All risk is extinction risk: All existential risks are risks of human extinction, so that no value will be realized after an existential catastrophe.

Under these assumptions, we can evaluate the expected value of the current world $W$, incorporating possible future continuations, as follows:

(Simple Model) $V\left[W\right]=v\sum _{i=1}^{\infty }(1-r{)}^i=v(1-r)/r.$

On this model, the value of our world today depends on the value $v$ of a century of human existence as well as the risk $r$ of existential catastrophe. Setting $r$ at a pessimistic $20\%$ values the world at a mere four times the value of a century of human life, whereas an optimistic risk of $0.1\%$ values the world at the value of nearly a thousand centuries.

But we're not interested in the value of the world. We care about the value of existential risk mitigation. Suppose you can act to reduce existential risk in your own century. More concretely, you can take some action $X$ which will reduce risk this century by some fraction $f$, from $r$ to $(1-f)r$. How good is this action?

On the Simple Model, it turns out that $V\left[X\right]=fv$. This result is surprising for two reasons.

1. Pessimism is irrelevant: The value of existential risk mitigation is entirely independent of the starting level of risk $r$.
2. Astronomical value begone!: The value of existential risk mitigation is capped at the value $v$ of the current century. Nothing to sneeze at, but hardly astronomical.

That’s not good for the Pessimist. She’d like to do better by challenging assumptions of the model. Which assumptions would she have to challenge in order to square Pessimism with the Astronomical Value Thesis?

3 Modifying the Simple Model

In this section, I extend an analysis by Toby and Tom to consider four ways we might change the Simple Model. I argue that the last, adopting a Time of Perils Hypothesis, is the most viable. I also place constraints on the versions of the Time of Perils Hypothesis that are strong enough to do the trick.

3.1 Absolute versus relative risk reduction

In working through the Simple Model, we considered the value of reducing existential risk by some fraction $f$ of its original amount. But this might seem like comparing apples to oranges. Reducing existential risk from 20% to 10% may be harder than reducing existential risk from 2% to 1%, even though both involve reducing existential risk to half of its original amount. Wouldn’t it be more realistic to compare the value of reducing existential risk from 20% to 19% with the value of reducing risk from 2% to 1%?

More formally, we were concerned about relative reduction of existential risk from its original level $r$ by the fraction $f$, to $(1-f)r$. Instead, the objection goes, we should have been concerned with the value of absolute risk reduction from $r$ to $r-f$. Will this change help the Pessimist?

It will not! On the Simple Model, the value of absolute risk reduction is $fv/r$. Now we have:

1. Pessimism is harmful: The value of existential risk mitigation grows inversely with the starting level $r$ of existential risk. If you are 100$\times$ as pessimistic as I am, you should be 100$\times$ less enthusiastic than I am about absolute risk reduction of any fixed magnitude.
2. Astronomical value is still gone: The value of existential risk mitigation remains capped at the value v of the current century.

That didn’t help. What might help the Pessimist?

3.2 Value growth

The Simple Model assumed that each additional century of human existence has some constant value $v$. That’s bonkers. If we don’t mess things up, future centuries may be better than the current century. These centuries may support higher populations, with longer lifespans and higher levels of welfare. What happens if we modify the Simple Model to build in value growth?

Value growth will certainly boost the value of existential risk mitigation. But it turns out that value growth alone is not enough to square Existential Risk Pessimism with the Astronomical Value Thesis. We’ll also see that the more value growth we assume, the more antagonistic Pessimism becomes to the Astronomical Value Thesis.

Let $v$ be the value of the present century. Toby and Tom consider a model on which value grows linearly over time, so that the value of the $N_{th}$ century from now will be $N$ times as great as the value of the present century, if we live to reach it.

(Linear Growth) $V\left[W\right]=v\sum _{i=1}^{\infty }i(1-r{)}^i=v(1-r)/r^2$

On this model, the value of reducing existential risk by some (relative) fraction $f$ is $fv/r$. Perhaps you think Toby and Tom weren’t generous enough. Fine! Let’s square it. Consider quadratic value growth, so that the $N_{th}$ century from now is $N^2$ times as good as this one.

(Quadratic Growth) $V\left[W\right]=v\sum _{i=1}^{\infty }{i}^2(1-r{)}^i=v(1-r\left)\right(2-r)/r^3.$

On this model, the value of reducing existential risk by $f$ is $fv(2-r)/r^2$. How do these models behave?

To see the problem, consider the value of a 10% (relative) risk reduction in this century (Table 1).

Table 1: Value of 10% relative risk reduction across growth models and risk levels

This table reveals two things:

1. Pessimism is (very) harmful: The value of existential risk mitigation decreases linearly (linear growth) or quadratically (quadratic growth) in the starting level of existential risk. This means that Existential Risk Pessimism emerges as a major antagonist to the Astronomical Value Thesis. If you are 100$\times$ as pessimistic as I am about existential risk, on the quadratic model you should be 10,000$\times$ less enthusiastic about existential risk reduction!
2. Astronomical Value Thesis is false given Pessimism: On some growth modes (i.e. quadratic growth) we can get astronomically high values for existential risk reduction. But we have to be less pessimistic to do it. If you think per-century risk is at 20%, existential risk reduction doesn’t provide more than a few times the value of the present century.

Now it looks reasonably certain that Existential Risk Pessimism, far from supporting the Astronomical Value Thesis, could well scuttle it. Let’s consider one more change to the Simple Model, just to make sure we’ve correctly diagnosed the problem.

3.3 Global risk reduction

The Simple Model assumes that we can only affect existential risk in our own century. This may seem implausible. Our actions affect the future in many ways. Why couldn’t our actions reduce future risks as well?

Now it’s not implausible to assume our actions could have measurable effects on risk in nearby centuries. But this will not be enough to save the Pessimist. On the Simple Model, cutting risk over the next $N$ centuries all the way to zero gives only $N$ times the value of the present century. To salvage the Astronomical Value Thesis, we would need to imagine that our actions today can significantly alter levels of existential risk across very distant centuries. That is less plausible. Are we to imagine that institutions founded to combat risk today will stand or spawn descendants millions of years hence?

More surprisingly, even if we assume that actions today can significantly lower existential risk across all future centuries, this assumption may still not be enough to ground an astronomical value for existential risk mitigation. Consider an action $X$which reduces per-century risk by the fraction $f$ in all centuries, from $r$ to $(1-f)r$ each century. On the Simple Model, the value of $X$ is then $\frac{f}{1-f}\frac{v}{r}$. What does this imply?

First, the good news. In principle the value of existential risk reduction is unbounded in the fraction $f$ by which risk is reduced. No matter how small the value v of a century of life, and no matter how high the starting risk $r$, a 100% reduction of risk across all centuries carries infinite value, and more generally we can drive value as high as we like if we reduce risk by a large enough fraction.

Now, the bad news.

1. The Astronomical Value Thesis is still probably false: Even though the value of existential risk reduction is in principle unbounded, in practice it is unlikely to be astronomical. To illustrate, setting risk $r$ to a pessimistic 20% values a 10% reduction in existential risk across all centuries at once at a modest $5v/9$. Even a 90% reduction across all centuries at once is worth only 45 times as much as the present century.
2. Pessimism is still a problem: At the risk of beating a dead horse, the value of existential risk reduction varies inversely with $r$. If you’re $100\times$ as pessimistic as I am, you should be $100\times$ less hot on existential risk mitigation.

Now it’s starting to look like Existential Risk Pessimism is the problem. Is there a way to tone down our pessimism enough to make the Astronomical Value Thesis true? Why yes! We should be Pessimists about the near future, and optimists about the long-term future. Let’s see how this would work.

3.4 The Time of Perils

Pessimists often think that humanity is living through a uniquely perilous period. Rapid technological growth has given us the ability to quickly destroy ourselves. If we learn to manage the risks posed by new technologies, we will enter a period of safety. But until we do this, risk will remain high.

Here’s how Carl Sagan put the point:

It might be a familiar progression, transpiring on many worlds … life slowly forms; a kaleidoscopic procession of creatures evolves; intelligence emerges … and then technology is invented. It dawns on them that there are such things as laws of Nature … and that knowledge of these laws can be made both to save and to take lives, both on unprecedented scales. Science, they recognize, grants immense powers. In a flash, they create world-altering contrivances. Some planetary civilizations see their way through, place limits on what may and what must not be done, and safely pass through the time of perils. Others [who] are not so lucky or so prudent, perish. (Sagan 1997, p. 173).

Following Sagan, let the Time of Perils Hypothesis be the view that existential risk will remain high for several centuries, but drop to a low level if humanity survives this Time of Perils. Could the Time of Perils Hypothesis save the Pessimist?

To math it up, let $N$ be the length of the perilous period: the number of centuries for which humanity will experience high levels of risk. Assume we face constant risk $r$ throughout the perilous period, with $r$ set to a pessimistically high level. If we survive the perilous period, existential risk will drop to the level $r_l$ of post-peril risk, where $r_l$ is much lower than $r$.

On this model, the value of the world today is:

(Time of Perils) $V\left[W\right]=\sum _{i=1}^{N}v(1-r{)}^i+(1-r{)}^N{\sum }_i^{\infty }v(1-r_l{)}^i$

That works out to a mouthful:

but it’s really not so bad.

Let $V_{PERIL}={\Sigma }_{i=1}^{\infty }v(1-r{)}^i$ be the value of living in a world forever stuck at the perilous level of risk, and $V_{\text{SAFE}}=\sum _{i=1}^{\infty }v(1-r_l{)}^i$ be the value of living in a post-peril world. Let SAFE be the proposition that humanity will reach a post-peril world and note that $Pr\left(SAFE\right)=(1-r{)}^N$. Then the value of the world today is a probability-weighted average of the values of the safe and perilous worlds.

As the length $N$ of the perilous period and the perilous risk level $r$ trend upwards, the value of the world tends towards the low value $V_{PERIL}$ of the perilous world envisioned by the Simple Model. But as the perilous period $N$ shortens and the perilous risk $r$ decreases, the value of the world tends towards the high value $V_{SAFE}$ of a post-peril world. We’ll see the same trends when we think about the value of existential risk mitigation.

Let $X$ be an action which reduces existential risk in this century by the fraction $f$, and assume that the perilous period lasts at least one century. Then we have:

This equation decomposes the value of $X$ into two parts, corresponding to the expected increase in value (if any) that will be realized during the perilous and post-peril periods. The first term, $fv[1-(1-r{)}^N]$ is bounded above by v, so it won’t matter much. The Astronomical Value Thesis needs to pump up the second term, $r(1-r{)}^{N-1}f{V}_{SAFE}$, representing the value we could get after the Time of Perils. Call this the crucial factor.

How do we make the crucial factor astronomically large? First, we need the perilous period $N$ to be short. The crucial factor decays exponentially in $N$, so a long perilous period will make the crucial factor quite small. Second, we need a very low post-peril risk $r_l$. The value $V_{SAFE}$of a post-peril future is determined entirely by the level of post-peril risk, and we saw in Section 2 that this value cannot be high unless risk is very low.

To see the point in practice, assume a pessimistic 20% level of risk during the perilous period. Table 2 looks at the value of a 10% reduction in relative risk across various assumptions about the length of the perilous period and the level of post-peril risk.

Table 2: Value of 10% relative risk reduction against post-peril risk and perilous period length

Note that:

1. Short is sweet: With a short 2-century perilous period, the value of $X$ ranges from 1.6-160$v$, and may be astronomical once we build in value growth. But with a long 50-century perilous period, there isn’t much we can do to make the value of $X$ large.
2. Post-peril risk must be very low: Even if post-peril risk drops by 2,000% to 1% per century, the Astronomical Value Thesis is in trouble. We need risk to drop very low, towards something like 0.01%. Note that for the Pessimist, this is a reduction of 200,000%!

What does this mean for Pessimism and the Astronomical Value Thesis? It’s time to take stock.

3.5 Taking stock

So far, we’ve seen three things:

1. Across a range of assumptions, Existential Risk Pessimism tends to hamper, not support the Astronomical Value Thesis: The best-case scenario is the Simple Model, on which Pessimism is merely irrelevant to the Astronomical Value Thesis. On other models the value of risk reduction decreases linearly or even quadratically in our level of pessimism.
2. The most plausible way to combine Existential Risk Pessimism with the Astronomical Value Thesis is through the Time of Perils Hypothesis: The Simple Model doesn’t bear out the Astronomical Value Thesis. It’s not enough to think about absolute risk reduction; value growth; or global risk reduction. We need to temper our pessimism somehow, and the best way to do that is the Time of Perils Hypothesis: we’ll be Pessimists for a few centuries, then optimists thereafter.
3. Two features that a Time of Perils Hypothesis must have if it is going to vindicate the Astronomical Value Thesis: We need (a) a fairly short perilous period, and (b) a very low level of post-peril risk.

New question: why would you believe a Time of Perils Hypothesis with the required form?

One reason you might believe this is because you think that superintelligence will come along, and that if superintelligence doesn’t kill us all, it would radically and permanently lower the level of existential risk. Let’s set that aside as part of our conclusion and ask a weaker question: is there any other good way to ground a strong enough Time of Perils Hypothesis? I want to walk through two popular arguments and suggest that they aren’t enough to do the trick.

4 Space: The final frontier?

You might think that the Time of Perils will end as humanity expands across the stars. So long as humanity remains tied to a single planet, we can be wiped out by a single catastrophe. But if humanity settles many different planets, it may take an unlikely series of independent calamities to wipe us all out.

The problem with space settlement is that it’s not fast enough to help the Pessimist. To see the point, distinguish two types of existential risks:

1. Anthropogenic risks: Risks posed by human activity, such as greenhouse gas emissions and bioterrorism.
2. Natural risks: Risks posed by the environment, such as asteroid impacts and naturally occurring diseases.

It’s quite right that space settlement would quickly drive down natural risk. It’s highly unlikely for three planets in the same solar system to be struck by planet-busting asteroids in the same century. But the problem is that Pessimists weren’t terribly concerned about natural risk. For example, Toby Ord estimates natural risk in the next century at 1/10,000, but overall risk at 1/6. So Pessimists shouldn’t think that a drop in natural risk will do much to bring the Time of Perils to a close.

Could settling the stars drive down anthropogenic risks? Recall that the Pessimist needs a (a) quick and (b) very sharp drop in existential risk to bring the Time of Perils to an end. The problem is that although space settlement will help with some anthropogenic risks, it’s unlikely to drive a quick and very sharp drop in the risks that count.

Figure 1: Toby Ord’s (2020) estimates of anthropogenic risk

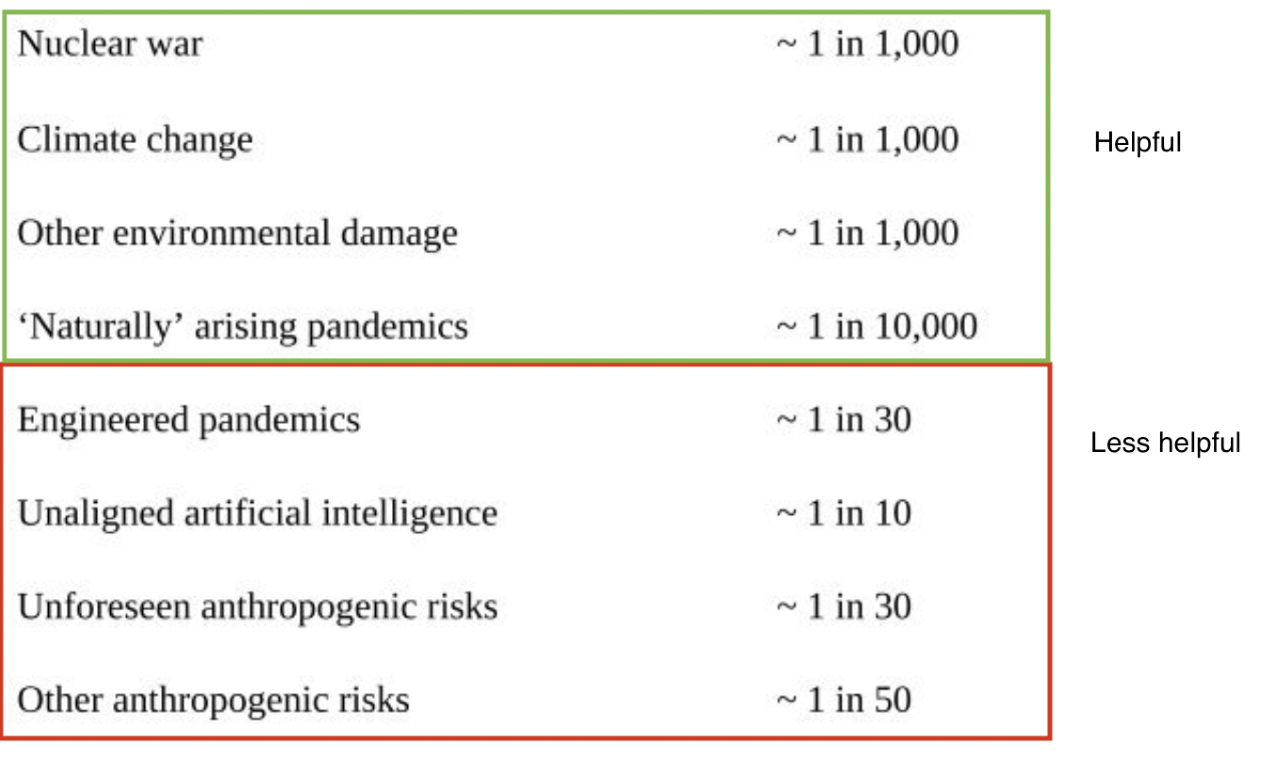
To see the point, consider Toby Ord’s estimates of the risk posed by various anthropogenic threats (Figure 1). Short-term space settlement would doubtless bring relief for the threats in the green box. After we’re done destroying this planet, we can always find another. And it is much easier to nuke Russia than it is to nuke Mars. But the Pessimist thinks that the threats in the green box are inconsequential compared to those in the red box. So we can’t bring the Time of Perils to an end by focusing on the green box.

What about the threats in the red box, such as AI risk and engineered pandemics? Perhaps long-term space settlement will help with these threats. It is not so easy to send a sleeper virus to Alpha Centauri. But we saw that the Pessimist needs a fast end to the Time of Perils, within the next 10-20 centuries at most. Could near-term space settlement reduce the threats in the red box?

Perhaps it would help a bit. But it’s hard to see how we could chop 3$-$4 orders of magnitude off these threats just by settling Mars. Are we to imagine that a superintelligent machine could come to control all life on earth, but find itself stymied by a few stubborn Martian colonists? That a dastardly group of scientists designs and unleashes a pandemic which kills every human living on earth, but cannot manage to transport the pathogen to other planets within our solar system? Perhaps there is some plausibility to these scenarios. But if you put 99.9% probability or better on such scenarios, then boy do I have a bridge to sell you.

So far, we have seen that banking on space settlement won’t be enough to ground a Time of Perils Hypothesis of the form the Pessimist needs. How else might she argue for the Time of Perils Hypothesis?

5 An existential risk Kuznets curve?

Consider the risk of climate catastrophe. Climate risk increases with growth in consumption, which emits fossil fuels. Climate risk decreases with spending on climate safety, such as reforestation and other forms of carbon capture.

Economists have noted that two dynamics push towards reduced climate risk in sufficiently wealthy societies. First, the marginal utility of additional consumption decreases, reducing the benefits of fossil fuel emissions. Second, as society becomes wealthier we have more to lose by destroying our climate. These dynamics exert pressure towards an increase in safety spending relative to consumption.

Some economists think that this dynamic is sufficient to generate an environmental Kuznets curve (Figure 2): an inverse U-shaped relationship between per-capita income and environmental degradation. Societies initially become wealthy by polluting their environments. But past a high threshold of wealth, rational societies should be expected to improve the environment more quickly than they destroy it, due to the diminishing marginal utility of consumption and the increasing importance of climate safety.

Figure 2: The environmental Kuznets curve. Reprinted from (Yandle et al. 2002).

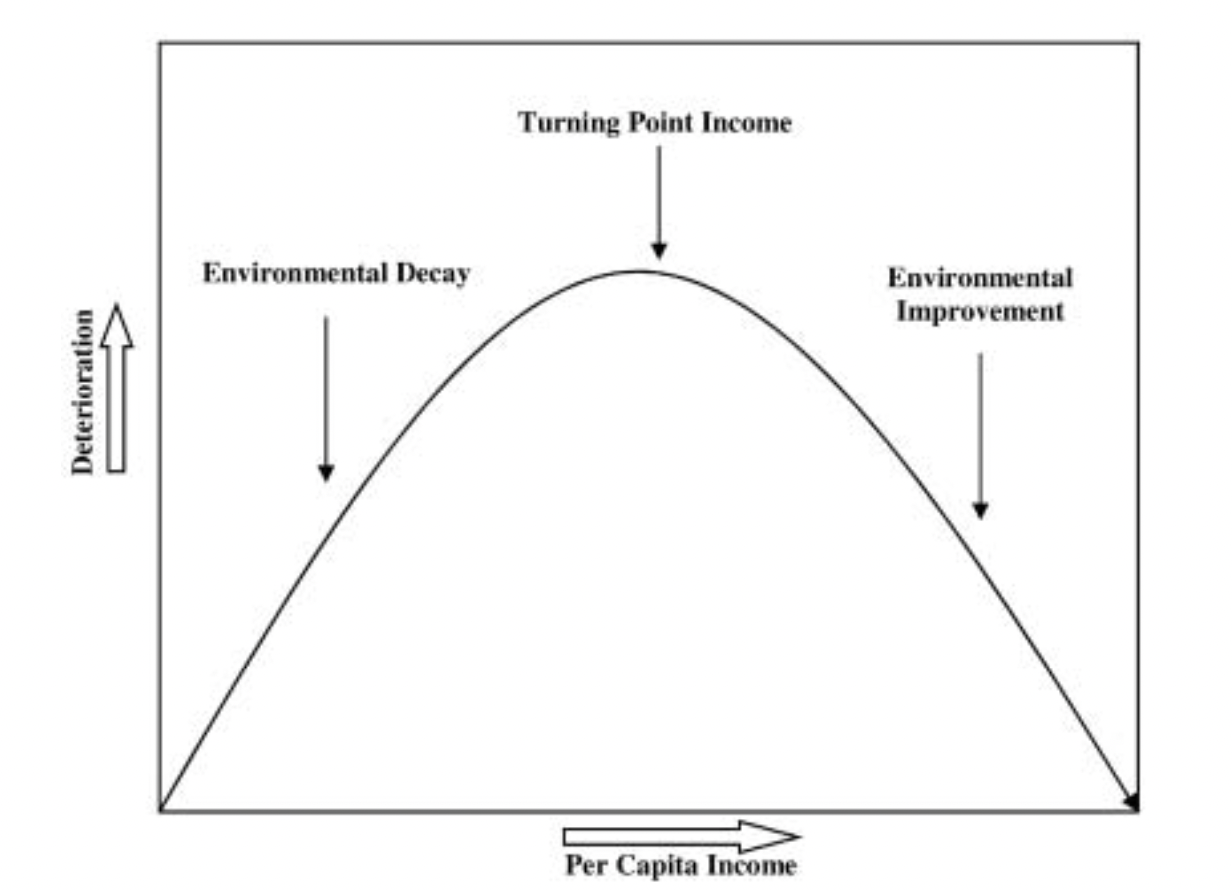
Now everyone admits that this dynamic is not fast enough to stop the world from causing irresponsible levels of environmental harm. We’ve already done that. But it may well be enough to prevent the most catastrophic warming scenarios, where 10-20${}^{\circ }$C warming may lead to human extinction or permanent curtailment of human potential.

Leopold Aschenbrenner (2020) argues that the same dynamic repeats for other existential risks. In Leopold’s model, society is divided into separate consumption and safety sectors. At time $t$, the consumption sector produces consumption outputs $C_t$ as a function of the current level of consumption technology $A_t$, and the labor force producing consumption goods $L_{ct}$:

Here $\alpha >0$ is a constant determining the influence of technology on production.

Similarly, the safety sector produces safety outputs $H_t$ as a function of safety technology $B_t$ and the labor force producing safety outputs $L_{ht}$:

As in the environmental case, Leopold takes existential risk ${\delta }_t$ to increase with consumption outputs and decrease with safety outputs. In particular, he assumes:

for constants $\overline{\delta },ϵ,\beta$.

Leopold proves that under a variety of conditions, optimal resource allocation should lead society to invest quickly enough in safety over consumption to drive existential risk towards zero. Leopold also shows that under a range of assumptions, his model grounds an existential risk Kuznets curve: a U-shaped relationship between time and existential risk (Figure 3). Although existential risk remains high today and may increase for several centuries, eventually the diminishing marginal utility of consumption and the increasing importance of safety should chase risk exponentially towards zero. Until that happens, humanity remains in a Time of Perils, but afterwards, we should expect low levels of post-peril risk continuing indefinitely into the future.

Figure 3: The existential risk Kuznets curve. Reprinted from (Aschenbrenner 2020).

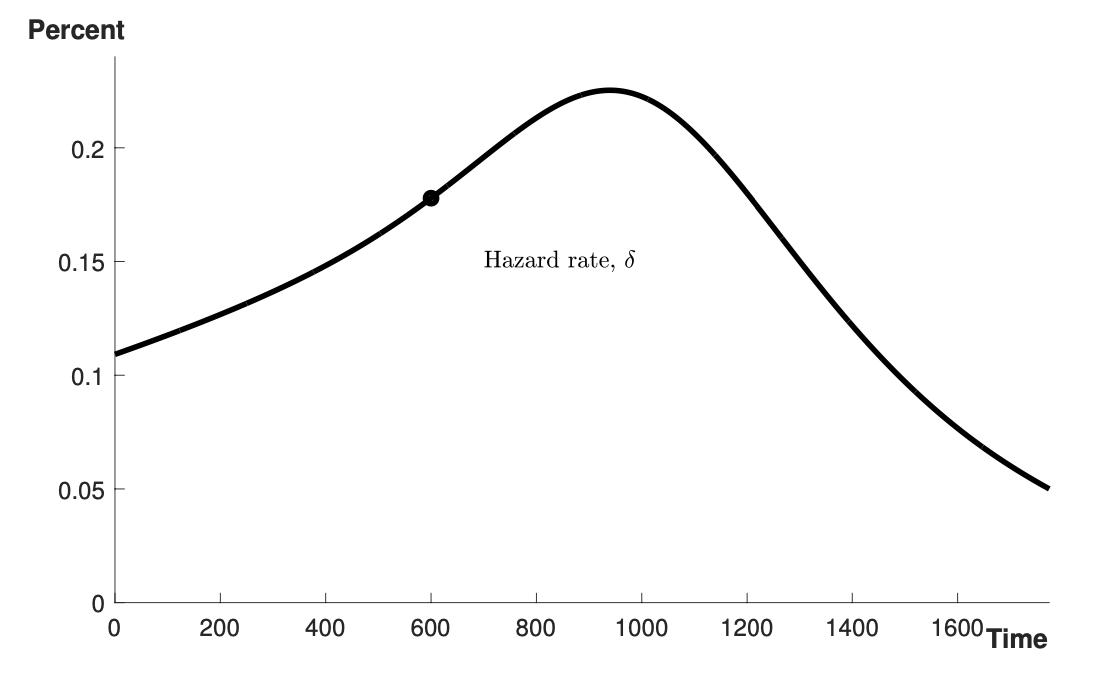
I think this is among the best arguments for the Time of Perils hypothesis. But I don’t think the model will save the Pessimist, because it disagrees with the Pessimist about the source of existential risk.

Leopold’s model treats consumption as the source of existential risk. But most Pessimists do not think that consumption is even the primary determinant of existential risk. In the special case of climate risk, consumption does indeed drive risk by emitting fossil fuels and causing other forms of environmental degradation. But Pessimists think most existential risk comes from things like rogue AI and engineered pandemics. These risks aren’t caused by consumption. They’re caused by technological growth. Risks from superintelligence grow with advances in technologies such as machine learning, and bioterrorism risks grow with advances in our capacity to synthesize, analyze and distribute biological materials. So a reduction in existential risk may be largely achieved through slowing growth of technology rather than slowing consumption.

We could revise (3) to let technologies A and B replace consumption outputs C as the main drivers of existential risk. But if we did this, we would lose all of the main theorems of the model, and hence we would not get a Time of Perils Hypothesis of the form we need.

6 What we’ve seen so far

Previously, we saw that:

1. Across a range of assumptions, Existential Risk Pessimism tends to hamper, not support the Astronomical Value Thesis.
2. The most plausible way to combine Existential Risk Pessimism with the Astronomical Value Thesis is through the Time of Perils Hypothesis.
3. The right Time of Perils Hypothesis must have (a) a fairly short perilous period, and (b) a very low level of post-peril risk.

Then we asked: is this form of the Time of Perils Hypothesis true? In the previous two sections, we saw that:

1. Arguments for the Time of Perils Hypothesis which do not appeal to AI are not strong enough to ground the relevant kind of Time of Perils Hypothesis: It won’t do to bank on space settlement, because that won’t do enough to solve the most pressing anthropogenic risks. And we can’t give a Kuznets-style economic argument for the Time of Perils Hypothesis without disagreeing with the Pessimist about the root causes of existential risk.

If that is right, then what might it imply for existential risk as a cause area?

7 Implications for existential risk mitigation as a cause area

To a large extent, these implications are up for discussion. But here are some things I think we might conclude from the discussion in this post.

1. Optimism helps: If you’re an optimist about current levels of existential risk, you should think it’s even more important to reduce existential risk than if you’re a Pessimist. This has two important implications.
   1. Mistargeted pushback: A common reaction to existential risk mitigation is that it can’t be very important, because levels of existential risk are actually much lower than EAs take them to be. All of the models in this paper strongly suggest that this reaction misses the mark. Within reason, the lower you think that existential risk is, the more enthusiastic you should be about reducing it.
   2. Danger for Pessimists: On the other hand, there is a live danger that existential risk mitigation may not be so valuable for Pessimists.
2. Cooling (slightly) on the Astronomical Value Thesis: Across the board, the models in this post suggest that it is harder than many EAs might think to support the Astronomical Value Thesis. The Astronomical Value Thesis could well be true, but it isn’t obvious.
   1. Warming (slightly) on short-termist cause areas: If that is right, then it is less obvious than it may seem that existential risk mitigation is always more valuable than short-termist causes such as global health and poverty.
3. The Time of Perils Hypothesis is very important: Pessimists should think that settling the truth value of the Time of Perils Hypothesis is one of the most crucial outstanding research questions facing humanity today. If the Time of Perils Hypothesis is false, then Pessimists may have to radically change their opinion of existential risk mitigation as a cause area.
4. But what about AI?: One way that EAs often argue for the Time of Perils Hypothesis is by arguing that superintelligent AI will soon be developed, and once superintelligence arrives it will have the foresight to drive existential risk down to a permanently low level. If I am right that other prominent ways of arguing for the Time of Perils Hypothesis are not successful, then the story about superintelligence becomes more important. This suggests that it is even more important than before to make sure we have the correct view about the likelihood of superintelligence bringing an end to the Time of Perils.

8 Key uncertainties

In the spirit of humility, I think it is important to end with a discussion of some uncertainties in my post.

1. Modeling assumptions: I’ve tried to be as generous as possible in thinking of ways to square Pessimism with the Astronomical Value Thesis. I’ve only found one model that works, the Time of Perils model. But I could well have missed other models that work. I’d be very interested to see them!
2. Fancier math: I’ve kept the models fairly simple, for example using discrete rather than continuous models, and treating quantities like risk as constants rather than variables. I think my conclusions are robust to some ways of making the models fancier, but I’m not sure if they’re robust to all ways of making the models fancier. If they’re not, that could be bad.
3. Arguments for the Time of Perils Hypothesis: I’ve only considered two arguments for the Time of Perils Hypothesis. There are others (wisdom, anyone?) that I didn’t address. Perhaps these are very good arguments.
4. Drawing conclusions: Are the implications that I draw for existential risk mitigation as a cause area well supported by the models? Are there other implications that might be worth considering?
5. Unknown unknowns: No author is a perfect judge of where they might have gone wrong. Most of us are quite poor judges of this. I am sure that I made, or could have made mistakes that I have not even considered.

What do you think?

9 Acknowledgments

Thanks to Tom Adamczewski, Gustav Alexandrie, Tom Bush, Tomi Francis, David Holmes, Toby Ord, Sami Petersen, Carl Shulman, and Phil Trammell for comments on this work. Thanks to audiences at the Center for Population-Level Bioethics, EAGxOxford and the Global Priorities Institute for comments and discussion. Thanks to Anna Ragg, Rhys Southan and Natasha Oughton for research assistance.

Appendix (Proofs)

The Simple Model

(Simple Model) $V\left[W\right]=v\sum _{i=1}^{\infty }(1-r{)}^i.$

Note that $V\left[W\right]$ is a truncated geometric series so that: 

Let $X$ be an intervention reducing risk in this century to $(1-f)r$, and let $W_X$ be the result of performing $X$. Then

And hence:

Absolute risk reduction

Let $X_{\text{ABS}}$ be an intervention reducing risk in this century to $r-f$ for $f\le r$. Then:

So that:

Linear growth

(Linear Growth) $V\left[W\right]=v\sum _{i=1}^{\infty }i(1-r{)}^i.$

Note that $V\left[W\right]$ is a polylogarithm with order $-1$. Recalling that 

 we have: 

If $X$ produces a relative reduction of risk by $f$ then:

So that: