The classical definition of democracy is “rule of majority with respect to the minority”. But the classics perfectly knew how oppressive can be the 51% of people over the rest and how difficult is to implement “respect”. I simply reject the majoritarian principle: democracy shall be about the rule of all, that is about optimizing the social system for the average of all preferences. More or less hard to implement, that is the ethical principle, and institutions shall be judged by that principle.
In the second section of this article, I summarize how the concept of “general interest” can be rescued after the Arrow impossibility result. In the third section I comment on the problems of direct democracy, and why parliaments need to delegate to a unitary government the administration of the State (that is, why majoritarianism is to some extent still inevitable). And in the final section of this note I move into practical politics, proposing some cases where parliaments shall decide by “averaging” instead of by majority, and ask the gentle reader to expand my proposed list, because averaging and sortition are often better (and no less legitimate) than majority rule.
The general interest
In decision theory textbooks a famous result (the “Arrow impossibility theorem”, Arrow, 1951) suggests that the general interest is impossible even to be defined. But a theorem is not a truth about external reality, but a truth about a given formal system. The Arrow theorem is true if preferences are ordinal and there is a single election. With cardinal preferences and multiple votes there is no “impossibility” theorem.
Suppose there is a set (X) of “attainable” states of the World . Naive cardinal utilitarianism suggest that given an aggregation functionW(.)-often simply a sum- and J members of the society each with a (possibly different) utility cardinal function on the states of the World, the social optimum is simply the point (attainable state of the world) that maximizes aggregate utility:
Unfortunately, this kind of optimization depends on absolute level of utility: more “sensitive” individuals (those whose utility function are cardinally larger) are given more “rights” under “cardinal utilitarianism”, but there is no way to know who is more sensitive because consciousness is noumenal. As long as the absolute levels of utility matter, utilitarianism is between wrong and simply useless (it depends on the deepest unobservable).
To deal with this, we shall recognize that interpersonal utility comparison is a political decision. In the modern democratic world, our main constitutional choice is the “one man, one vote” principle: in utilitarian parlance we suppose all people are equally sensitive and equally valuable and equal political rights are given to all. This supposition implies first “utility normalization” (Dhillon, Bouveret Lemaître, 1999), and only after utility normalization aggregate welfare maximization.
In practice, for a single vote, the Arrow theorem perchlorates into the “cardinal normalized preferences” framework because in a single election there is no way you can signal preference intensity. The escape from Arrow impossibility (as was already suggested in Buchanan, 1962) depends on multiple and related elections (Casella and Macè, 2021).
Casella (2005) proposed the Storable Votes (SV) voting mechanism, where participants in a sequence of elections are given additional votes in each period, so they can signal the intensity of their preferences and avoid the disenfranchisement of minorities that comes from simple majority voting. Shortly after the introduction of SV, Jackson & Sonnenschein (2007) proved that connecting decisions over time can resolve the issue of incentive compatibility in a broad range of social choice problems.
Macias (2024a) proposed the “Storable Votes-Pay as you win” (SV-PAYW) mechanism where a fixed number of storable votes are used to decide on a sequence of elections, but only votes casted on the winning alternative are withdrawn from the vote accounts of each player (and those wining votes are equally redistributed among all participants). In a simulation environment this kind of “auction like” version of the SV mechanism allowed for minority view integration into the democratic process with only a very modest deviation from social optimality.
Why government?
If political decisions were sequential and independent, SV-PAYW probably (we have no theorems, only numerical simulations) would solve the preference aggregation problem, and Arrow’s problem could be considered overcame with no need of government (assembly rule, either direct or representative would be efficient). Unfortunately, political decisions are far from “sequential and independent”. Portfolios of policies have synergies and independent choice of policies can lead to suboptimal outcomes. That is why assembly rule is unusual and parliaments always appoint a government. It also explains why SV-PAYW was not discovered and applied centuries ago.
In the “Ideal Political Workflow” (Macias, 2024b), I suggested that in the perfect democracy, people would vote in the space of “outcomes” not in the space of “policies”, avoiding by that expedient the “political coherence problem”, but that is only possible if the relation between “policies” and “outcomes” is well known. Unfortunately, often matters of fact are politicized and/or are not well understood.
For the time being, the Ideal Political Workflow will remain… ideal.
Separable decisions and non-majoritarian rules
But sometimes decisions are separable. For example, decisions on private consumption are so separable that we can leave them mostly to households and firms (that is the meaning of the two theorems on welfare economics).
For some separable decisions, in my view parliaments shall decide not by majority, but by averaging (or rank voting).
NGO subsidy allocation: Let’s suppose a national parliament has a given Budget for NGO Support. A natural way to allocate those funds is to allow each parliamentarian to propose a complete disclosure and take the simple average: if NGO “Save the Shrimps” get a 20% proposed allocation from the 10% of members of parliament, they shall receive a 2% of total NGO funds.
Infrastructure expenditure: Other parts of the budget perhaps shall also be chosen by averaging (for example, can funds for public infrastructure be allocated by a sharing system, instead of majority? Doing so would imply having structures of technical support in the ministry of Infrastructure for different parliamentarian groups).
Judicial nomination: in the US, the president and the Senate chose the judges. In my view, ranked vote would allow the construction of a list of judicial appointees that (closely) replicates parliamentary composition, instead of being chosen by the wining party. Adding sortition as a mechanism for Higher Courts, the judicial system would be much more robust to political capture.
Public media control: in Italy, the RAI channels are allocated to different political parties (RAI1 is right wing and RAI3 is left wing).
Averaging gives power to every member of parliament, avoiding minority disenfranchisement. Now, gentle reader, what else? What other issues shall a Parliament decide by average/ranked voting/sharing instead of by majority and which concrete rule do you favor?
References
Arrow, K.J. (1951). Social Choice and Individual Values. New York: Wiley,
Buchanan, J.M. (1962). The Calculus of Consent. Ann Arbor: Univ.Mich.Press
Casella, A. (2005). Storable Votes, Games and Economic Behavior. https://doi.org/10.1016/j.geb.2004.09.009
Casella, A., Macè, A. (2021). Does Vote Trading Improve Welfare?, Annual Review of Economics. https://doi.org/10.1146/annurev-economics-081720-114422
Dhillon, A., Bouveret, S.,Lemaître, M. (1999). Relative Utilitarianism. Econometrica. https://doi.org/10.1111/1468-0262.00033
Jackson M.O.,Sonnenschein H.F. (2007). Overcoming incentive constraints by linking decisions, Econometrica. https://doi.org/10.1111/j.1468-0262.2007.00737.x
Macías, A. (2024a). Storable votes with a pay-as-you-win mechanism, Journal of Economic Interaction and Coordination. Ungated version: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4326247
Macías, A. (2024b). The Ideal Political workflow. SSRN

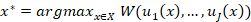
Hi Arturo,
You might be interested in this graph, from me and Jobst's paper: "Should we vote in non-deterministic elections?"
It visualizes the effective power groups of voters have in proportion to their percentage of the votes. So for most winner-takes-all systems (conventional voting systems) it is a step function; if you have 51% of the vote you have 100% of the power (blue line).
Some voting systems try to ameliorate this by requiring a supermajority; e.g. to change the constitution you need 2/3rds of the votes. This slows down legislation and also doesn't really change the problem of proportionality.
Our paper talks about non-deterministic voting systems, systems that incorporate an element of chance. The simplest version would be the "random ballot"; everyone sends in their ballot, then one is drawn at random. This system is perfectly proportional. A voting bloc with 49% of the votes is no longer in power 0% of the time, but is now in power 49% of the time (green line).
Of course not all non-deterministic voting systems are as proportional as the random ballot. For example, say that instead of picking one ballot at random, we keep drawing ballots at random until we have two that pick the same candidate. Now you get something in between the random ballot and a conventional voting systems (red line).
There are an infinite amount of non-deterministic voting systems so these are just two simple examples and are not the actual non-deterministic voting systems we endorse. For a more sophisticated non-deterministic voting system you can take a look at MaxParC.
Also, as you may have noticed, EAs are mostly focused on individualistic interventions and are not that interested in this kind of systemic change (I don't bother with my papers on this forum). If you want to discuss these types of ideas you might have more luck on the voting subreddit, the voting theory forum, or the electo wiki.
First of all, thanks for the suggestion. I will post this in the "Voting Theory Forum" (for papers I am also a participant in the "Decision Theory Forum"), and probably in electo wiki (the reddit looks too entropic).
I will read your paper and contact (by mail) you and Dr. Heitzig, including the gated version of my paper and some additional material and probably I will consult you on my next steps.
In any case, as commented before, in my view there is a massive difference between static voting and dynamic voting. With a single vote, Arrow is inevitable. When you vote many times in the i.i.d framework, you can communicate preference intensities, and the Arrow problem can be addressed. Unfortunately, when decisions interact, policy coordination by simple (sequential) voting looks intractable to me.
Thank you very much for your comment,
Arturo
Executive summary: Democracy should optimize for average preferences rather than majority rule, and parliaments should use averaging or ranked voting instead of majoritarianism for certain separable decisions.
Key points:
This comment was auto-generated by the EA Forum Team. Feel free to point out issues with this summary by replying to the comment, and contact us if you have feedback.