Suppose someone tries to convince you to give them $5, with the following argument:
Pascal’s Mugger: “I’m actually a traveller from another dimension, where 10^10^10^10 lives are in danger! Quick, I need $5 to save those lives, no time to explain! I don’t expect you to believe me, of course, but if you follow the expected utility calculation, you’ll give me the money—because surely the probability that I’m telling the truth, while tiny, is at least 1-in-10^10^10^10.”
Now suppose someone tries to convince you to donate $5 to their organization, with the following argument:
Long-termist: “My organization works to prevent human extinction. Admittedly, the probability that your donation will make the difference between success and failure is tiny, but if it does, then you’ll save lives! And surely the probability is greater than 1-in-. So you are saving at least 1 life, in expectation, for $5—much better than the Against Malaria Foundation!”
Obviously, we should refuse the Mugger. Should we also refuse the long-termist, by parallel reasoning? In general, do the reasons we have to refuse the Mugger also count as reasons to de-prioritize projects that seem high-expected-value but have small probabilities of success—projects like existential risk reduction, activism for major policy changes, and blue-sky scientific research?
This article explores that question, along with the more general issue of how tiny probabilities of vast utilities (i.e. vast benefits) should be weighed in our decision-making. It draws on academic philosophy as well as research from the effective altruism community.
Summary
There are many views about how to handle tiny probabilities of vast utilities, but they all are controversial. Some of these views undermine arguments for mainstream long-termist projects and some do not. However, long-termist projects shelter within the herd of ordinary behaviors: It is difficult to find a view that undermines arguments for mainstream long-termist projects without also undermining arguments for behaviors like fastening your seatbelt, voting, or building safer nuclear reactors.
Amidst this controversy, it would be naive to say things like “Even if the probability of preventing extinction is one in a quadrillion, we should still prioritize x-risk reduction over everything else…”
Yet it would also be naive to say things like “Long-termists are victims of Pascal’s Mugging.”
Table of contents:
2. The initial worry: Does giving to the Mugger maximize expected utility?
4. Steelmanning the problem: funnel-shaped action profiles
5. Solutions exist, but some of them undermine long-termist projects
6. Sheltering in the herd: a defense of mainstream long-termist projects
2. The initial worry: Does giving to the Mugger maximize expected utility?
This section explains the problem in more detail, and in particular explains why “But the probability that Pascal’s Mugger is telling the truth is extremely low” isn’t a good solution.
Consider the following chart:
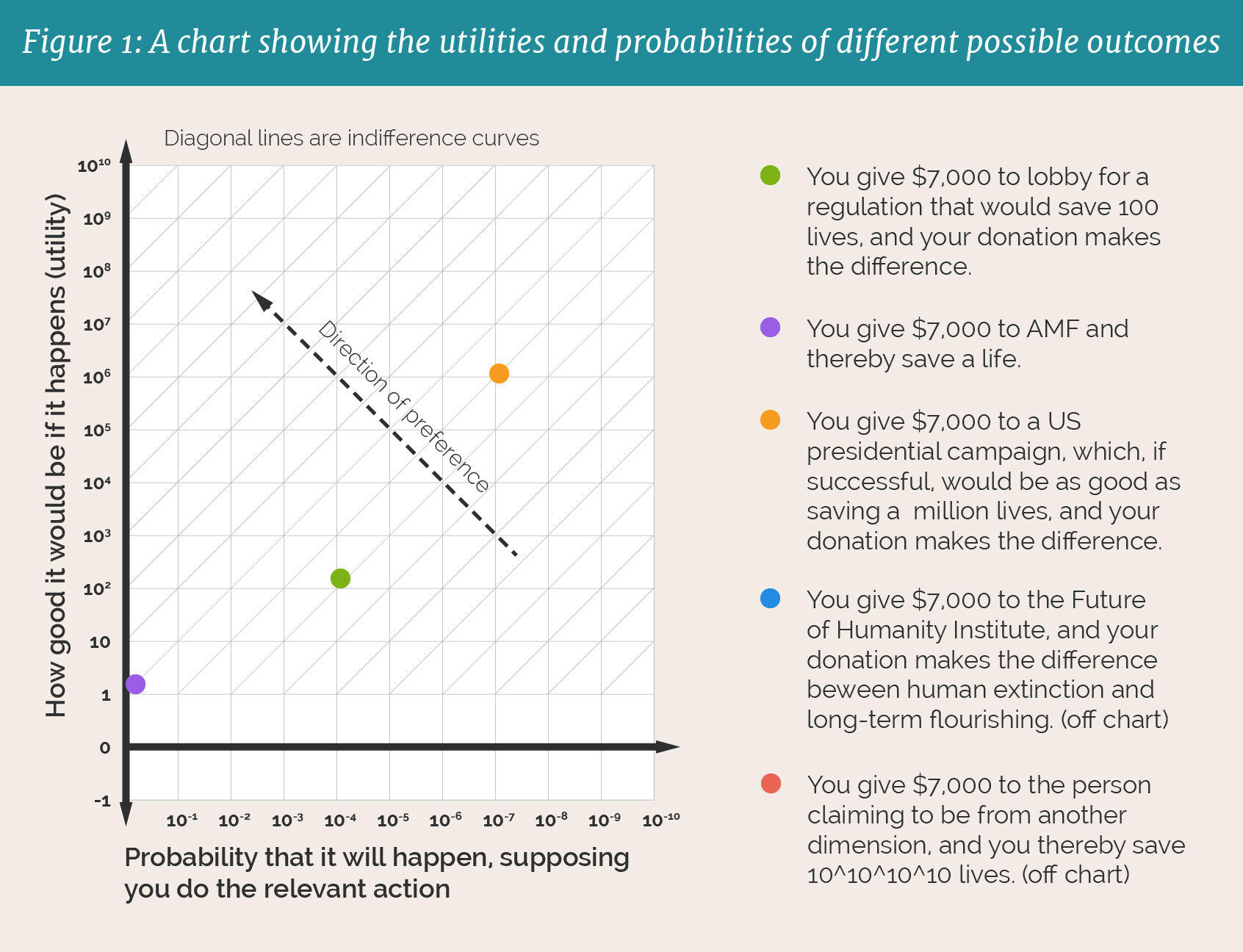
Each color is an action you are considering; each star is a possible outcome. Each possible outcome has a probability, i.e. the answer to the question “Supposing we do this action, what’s the probability of this happening?” Each possible outcome also has a utility, i.e. “Suppose we do it and this happens, how good would that be?”
If we obey expected utility calculations, we’ll be indifferent between, for example, getting utility 1 for sure and getting utility 100 with probability 0.01. Hence the blue lines: If we obey normal expected utility calculations, we’ll choose the action which is on the highest blue line.
You’ll notice that the red and blue stars are not on the chart. This is because they would be way off the currently shown portion. The long-termist caricatured earlier argues that the blue star should be placed at around —about thirty centimeters above the top of the chart—and hence that even if its probability is small, so long as it is above , it will be preferable to giving to AMF.
What about the Mugger? The red star should be placed far to the right on this chart; its probability is extremely tiny. How tiny do you think it is—how many meters to the right would you put it?
Even if you put it a billion light-years to the right on the chart, if you obey expected utility calculations, you’ll prefer it to all the other options here. Why? Because 10^10^10^10 is a very big number. The red star is farther above than it is to the right; the utility is more than enough to make up for the low probability.
Why is this so? Why isn’t the probability 0.1^10^10^10 or less? To some readers it will seem obvious—after all, if you made a bet you were this confident about every second until the end of the universe, surely there’s a reasonable chance you’d lose at least one of them, yet that would be that would be a mere 10^10^10 bets. Nevertheless, intuitions vary, and thus far we haven’t presented any particular argument that the red star is farther above than it is to the right. Unfortunately, there are several good arguments for that conclusion. For reasons of space, these are mostly in the appendix; for now, I’ll merely summarize one of the arguments.
Argument from hypothetical updates:
In a nutshell: 0.1^10^10^10 is such a small probability that no amount of evidence could make up for it; you’d continue to disbelieve no matter what happened. But that’s unreasonable:
Suppose that, right after the Mugger asks you for money, a giant hole appears in the sky and an alien emerges from it, yelling “You can’t run forever!” The Mugger then makes some sort of symbol with his hands, and a portal appears right next to you both. He grabs you by the wrist and pulls you with him as he jumps through the portal… Over the course of the next few days, you go on to have many adventures together as he seeks to save 10^10^10^10 lives, precisely as promised. In this hypothetical scenario, would you eventually come to believe that the Mugger was telling the truth? Or would you think that you’re probably hallucinating the whole thing?
It can be shown that if you decide after having this adventure that the Mugger-was-right hypothesis is more likely than hallucination, then before having the adventure you must have thought the Mugger-was-right hypothesis was significantly more likely than 0.1^10^10^10. (See appendix 8.1.1, to come) In other words, if you really think that the probability of the Mugger-was-right outcome is small enough, you would continue disbelieving the Mugger even if he takes you on an interdimensional adventure that seemingly verifies all his claims. Since you wouldn’t, you don’t.
Here is our problem: Long-termists admit that the probability of achieving the desired outcome (saving the world, etc.) by donating to them is small. Yet, since the utility is higher than the probability is small, the expected utility of donating to them is very high, higher than the expected utility of donating to other charitable causes like AMF. So, they argue, you should donate to them. The Mugger seems to be saying something very similar; the only difference seems to be that the probabilities are even smaller and the utilities are even larger. In fact, the utilities are so much larger that the expected utility of giving to the Mugger is much higher than the expected utility of giving to the long-termist! Insofar as we ought to maximize expected utility, it seems we should give money to the Mugger over the long-termist.
So (the initial worry goes) since the Mugger’s argument is obviously unacceptable, we should reject the long-termists’ argument as well: Expected utility arguments are untrustworthy. Barring additional reasons to give to the long-termist, we should save our money for other causes (like AMF) instead.
Next post in this series: Defusing the Initial Worry and Steelmanning the Problem
Notes:
1: For convenience throughout this article I will omit parentheses when chaining exponentials together, i.e. by 10^10^10^10 I mean 10^(10^(10^10)).
2: They’re called Pascal’s Mugger in homage to Pascal’s Wager. that the mugger is not waiting to see what probability you assign to his truthfulness and then picking N to beat that. This would not work, since the probability depends on what N is. The mugger is simply picking an extremely high N and then counting on your intellectual honesty to do the rest: do you really assign probability of less than 0.1^10^10^10, or are you just rationalizing why you aren’t going to give the money? More on this later. Note
3: Long-termism is roughly the idea that when choosing which causes to prioritize, we should be thinking about the world as a whole, not just as it is now, but as it will be far into the future, and doing what we think will lead to the best results overall. Because the future is so much bigger than the present, the long-term effects of our decisions end up mattering quite a lot in long-termist calculations. Common long-termist priorities are e.g. preventing human extinction, steering society away from harmful equilibria, and attempting to influence societal values in a long-lasting way. See here more. Note that not all long-termist projects involve tiny probabilities of success; it’s just that so far many of them do. Making a big-picture difference is hard. for
4: 10^40 lives saved by preventing human extinction is a number I made up, but it’s a conservative estimate; see https://nickbostrom.com/astronomical/waste.html Note that this assumes we don’t take a person-affecting view in population ethics. If we do, then they aren’t really “lives saved,” but rather “lives created,” and thus don’t count..
5: The author would like to thank Amanda Askell, Max Dalton, Yoaav Isaacs, Miriam Johnson, Matt Kotzen, Ramana Kumar, Justis Mills, and Stefan Schubert for helpful discussion and comments.
6: “Utility” is meant to be a non-loaded term. It is just a number representing how good the outcome is.
7: To see this, think of how high above the top of the chart the red star is. 10^10^10^10 lives saved is 10^10^10 centimeters or so above the top of the chart; that is, 10^10,000,000,000 centimeters. A billion light years, meanwhile, is ~10^27 centimeters.
8: This argument originated with Yudkowsky, though I’ve modified it slightly: http://lesswrong.com/lw/h8m/being_halfrational_about_pascals_wager_is_even/
9: This article only considers whether Pascal’s Mugging (and the more general problem it is an instance of) undermines the most prominent arguments given for causes like existential risk reduction, steering the future, etc.: expected utility calculations that multiply a large utility by a small probability. (This article will sometimes call these “long-termist arguments” for short.) However, there are other arguments for these causes, and also other arguments against. For example, take x-risk reduction. Here are some (sketches of) other arguments in favor: (A) We owe it to the people who fought for freedom and justice in the past, to ensure that their vision is eventually realized, and it’s not going to be realized anytime soon. (B) We are very ignorant right now, so we should focus on overcoming that—and that means helping our descendents be smarter and wiser than us and giving them more time to think about things. (C) Analogy: Just as an individual should make considerable sacrifices to avoid a 1% risk of death in childhood, so too should humanity make considerable sacrifices to avoid a 1% risk of extinction in the next century. And here are some arguments against: (A) We have a special moral obligation to help people that we’ve directly harmed, and those people are not in the future, (B) Morality is about obeying your conscience, not maximizing expected utility, and our consciences don’t tell us to prevent x-risk. I am not endorsing any of these arguments here, just giving examples of additional arguments one might want to consider when forming an all-things-considered view.

The examples in the post have expected utilities assigned using inconsistent methodologies. If it's possible to have long-run effects on future generations, then many actions will have such effects (elections can cause human extinction sometimes, an additional person saved from malaria could go on to cause or prevent extinction). If ludicrously vast universes and influence over them are subjectively possible, then we should likewise consider being less likely to get ludicrous returns if we are extinct or badly-governed (see 'empirical stabilization assumptions' in Nick Bostrom's infinite ethics paper). We might have infinite impact (under certain decision theories) when we make a decision to eat a sandwich if there are infinite physically identical beings in the universe who will make the same decision as us.
Any argument of the form "consider type of consequence X, which is larger than consequences you had previously considered, as it applies to option A" calls for application of X to analyzing other options. When you do that you don't get any 10^100 differences in expected utility of this sort, without an overwhelming amount of evidence to indicate that A has 10^100+ times the impact on X as option B or C (or your prior over other and unknown alternatives you may find later).
I believe this concern is addressed by the next post in the series. The current examples implicitly only consider two possible outcomes: "No effect" and "You do blah blah blah and this saves precisely X lives..." The next post expands the model to include arbitrarily many possible outcomes of each action under consideration, and after doing so ends up reasoning in much the way you describe to defuse the initial worry.
Thanks for the food for thought. I thought I'd share three related notes on framing which might be relevant to the rest of your series:
1) Tiny probabilities appear to not be fundamental to long-termism. The mugging argument you attribute to long-termists is indeed espoused as the key argument in favour by some, especially on online forums, but many people researching these problems assign non-mugging (e.g. ~1%) probability of their organizations having an overall large effect. For example, Yudkowsky in the interesting piece you linked (thanks for that):
It would be excellent to see someone write this up, since the divergence in argumentation by different parties interested in long-termism is large.
2) Projects tend not to have binary outcomes, and may have large potential positive and negative effects which have unclear sign on net. This makes robustness considerations (Knightian uncertainty, confidence in the sign, etc.) somewhere between quite important and the central consideration. This is the key reason why I pay little attention to the mugging arguments, which typically assume no negative outcomes without justifying this assumption. Instead, I think that the strongest case for aiming directly at improving the long-run may revolve around the robustness gained from aiming directly at where most of the expected value is (if one considers future generations to be morally relevant). Might be valuable to explore the relative merits of these approaches.
3) Consider explicitly separating the overall promisingness of a project from the marginal effect of additional resources. This is relevant e.g. for case 'You give $7,000 to the Future of Humanity Institute, and your donation makes the difference between human extinction and long-term flourishing.' i.e. consider separating out 'your donation makes the difference' from 'the Future of Humanity Institute has a large positive impact'. When looking at marginal contributions, these things can get conflated. For example, there is a low probability that there has been or will be a distribution of bednets which would not have happened had I not donated $3,000 to AMF in 2014, but this uncertainty does not worry me. Uncertainty about whether increasing economic growth is good is a much larger deal. It looks like Eliezer summarised this well:
Based on your 'Summary' section, I suspect that you are already intending to tackle some of these points in 'Sheltering in the herd' or elsewhere. Good luck!
Thanks for the comments--yeah, future posts are going to discuss these topics, though not necessarily using this terminology. In general I'm engaging at a rather foundational level: why is Knightian uncertainty importantly different from risk, and why is the distinction Yudkowsky mentions at the end a good and legitimate distinction to make?
Question for the author:
What did you -- or whoever the designer was -- use to make that chart? It's clear and attractive, and I'd love to know how to create something similar in the future.
I designed the charts, and am glad you appreciate them! I just used Adobe Illustrator, which is one of the best graphic design/vector-based programs. But in terms of creating something similar, it's a bit more about learning some graphic design than it is about knowing any particular set of steps or software.
It's not super hard to get good at making clean and clear data visualizations. I encourage you to just try some not-too-limiting software (like illustrator), arm yourself with it's user manual, some youtube tutorials, and references of visualizations you think are pleasant, and then simply play with some of your data to try and make it feel pleasant.
I share Kit's concerns about assuming binary outcomes, but I'd also like to add: Even if we assume that the outcome of a donation is binary (you have 0 impact with probability P, and X impact with probability 1-P), how can we tell what a good upper bound might be for the P we'd be willing to support?
Almost everyone would agree that Pascal's Mugging stretches the limits of credulity, but something like a 1-in-10-million chance of accomplishing something big isn't ridiculous on its face. That's the same order of magnitude as, say, swinging a U.S. Presidential election, or winning the lottery. Plenty of people would agree to take those odds. And it doesn't seem unreasonable to think that giving $7000 to fund a promising line of research could have a 1-in-10-million chance of averting human extinction.
--
Intuitively, I think my upper bound on P is linked in some sense to the scale of humanity's resources. If humanity is going to end up using, say, $70 billion over the next 20 years to reduce X-risk, that's enough to fund ten million $7,000 grants. If each of those grants has something like a 1-in-10-million chance of letting humanity survive, that feels like a good use of money to me. (By comparison, $70 billion is a little more than one year of U.S. foreign aid funding.) The same would still go for 1-in-a-billion chances, if that were really the best chances we had.
By comparison, if we only had access to 1-in-a-trillion chances, I'd be much more skeptical of X-risk funding, since under those odds we could throw all of our money at the problem and still be extraordinarily unlikely to accomplish anything at all.
Of course, we can't really tell whether current X-risk opportunities have odds in the range of 1-in-a-million, 1-in-a-billion, or even worse. But I think we're probably closer to "million" than "trillion", so I don't feel like I'm being mugged at all, especially if early funding can give us more information about our "true" odds and makes those odds better instead of worse.
(That said, I respect that others' intuitions differ sharply from mine, and I recognize that the "scale of humanity's resources" idea is pretty arbitrary.)
It's good to know lots of people have this intuition--I think I do too, though it's not super strong in me.
Arguably, when p is below the threshold you mention, we can make some sort of psuedo-law-of-large-numbers argument for expected utility maximization, like "If we all follow this policy, probably at least one of us will succeed." But when p is above the threshold, we can't make that argument.
So the idea is: Reject expected utility maximization in general (perhaps for reasons which will be discussed in subsequent posts!), but accept some sort of "If following a policy seems like it will probably work, then do it" principle, and use that to derive expected utility maximization in ordinary cases.
All of this needs to be made more precise and explored in more detail. I'd love to see someone do that.
(BTW, upcoming posts remove the binary-outcomes assumption. Perhaps it was a mistake to post them in sequence instead of all at once...)
In footnote 2 you ask:
I find myself asking the opposite whenever someone says they have a very very large good outcome. Didn't they just make up the amount of really large bigness as an attempt to preempt your assignment of a small probability?
Thanks for the interesting post. One thought I have is developed below. Apologies that it only tangentially relates to your argument, but I figured that you might have something interesting to say.
Ignoring the possibility of infinite negative utilities. All possible actions seem to have infinite positive utility in expectation. For all actions have a non-zero chance of resulting in infinite positive utility. For it seems that for any action there's a very small chance that it results in me getting an infinite bliss pill, or to go Pascal's route to getting into an infinitely good heaven.
As such, classic expected utility theory won't be action guiding unless we add an additional decision rule: that we ought to pick the action which is most likely to bring about the infinite utility. This addition seems intuitive to me, imagine two bets: one where there is 0.99 chance of getting infinite utility and one where there is a 0.01 chance. It seems irrational to not take the 0.99 deal even though they have the same expected utility.
Now lets suppose that the mugger is offering infinite expected utility rather than just very high utility. If my argument above is the case then I don't think the generic mugging case has much bite.
It doesn't seem very plausible that donating my money to the mugger is a better route to the infinite utility than say attempting to become a Muslim in case heaven exists or donating to an AI startup in the hope that a superintelligence might emerge that would one day give me an infinite bliss pill.
I and most other people (I'm pretty sure) wouldn't chase the highest probability of infinite utility, since most of those scenarios are also highly implausible and feel very similar to Pascal's mugging.
So my claim I'm trying to defend here is not that we should be willing to hand over our wallet in Pascal's mugging cases.
Instead its a conditional claim that if you are the type of person who finds the Mugger's argument compelling then then the logic which leads you to find it compelling actually gives you reason not to hand over your wallet as there are more plausible ways of attempting to elicit the infinite utility than dealing with the mugger.
I see, that makes sense, and I agree with it.
Another argument to be aware of is that it is a bad idea decision-theoretically to pay up, since anyone can then mug you, and you lose all of your money, argued in Pascal's Muggle Pays. On the face of it, this is compatible with expected utility maximization, since you would predictably lose all of your money if there are any adversaries in the environment by following the policy of paying the mugger. However, comments on that post argue against this by saying that even the expected disutility from being continually exploited forevermore would not balance out the huge positive expected utility from paying the mugger, so you would still pay the mugger.
Yup. Also, even if the decision-theoretic move works, it doesn't solve the more general problem. You'll just "mug yourself" by thinking up more and more ridiculous hypotheses and chasing after them.
Interesting post!
I am quite interested in your other arguments for why EV calculations won't work for pascal's mugging and why they might extend to x-risks. I would probably have prefered a post already including all the arguments for your case.
About the argument from hypothetical updates: My intuition is, that if you assign a probability of a lot more than 0.1^10^10^10 to the mugger actually being able to follow through this might create other problems (like probabilities of distinct events adding to something higher than 1 or priors inconsistent with occams razor). If that intuition (and your argument) was true (my intuition might very well be wrong and seems at least slightly influenced by motivated reasoning), one would basically have to conclude that bayesian EV reasoning fails as soon as it involves combinations of extreme utilities and miniscule probabilities.
However, i don't think the credenced for being able to influence x-risks are so low, that updating becomes impossible and therefore i'm not convinced not to use EV to evaluate them by your first argument. I'm quite eager to see the other arguments, though.
Thanks! Yeah, sorry--I was thinking about putting it up all at once but decided against because that would make for a very long post. Maybe I should have anyway, so it's all in one place.
Well, I don't share your intuition, but I'd love to see it explored more. Maybe you can get an argument out of it. One way to try would be to try to find a class of at least 10^10^10^10 hypotheses that are at least as plausible as the Mugger's story.
Very interesting - by pure chance I spent this morning thinking about this topic (from a position of relative ignorance). I look forward to the rest of the series!