Summary
Evidential cooperation in large worlds (ECL) is a proposed way of reaping gains—that is, getting more of what we value instantiated—through cooperating with agents across the universe/multiverse. Such cooperation does not involve physical, or causal, interaction. ECL is potentially a crucial consideration because we may be able to do more good this way compared to the “standard” (i.e., causal) way of optimizing for our values.
The core idea of ECL can be summarized as:
- According to non-causal decision theories, my decisions relevantly “influence” what others who are similar to me do, even if they never observe my behavior (or the causal consequences of my behavior). (More.)
- In particular, if I behave cooperatively towards other value systems, then other agents across the multiverse are more likely to do the same. Hence, at least some fraction of agents can be (acausally) influenced into behaving cooperatively towards my value system. This gives me reason to be cooperative with other value systems. (More.)
- Meanwhile, there are many agents in the universe/multiverse. (More.) Cooperating with them would unlock a great deal of value due to gains from trade. (More.) For example, if I care about the well-being of sentient beings everywhere, I can “influence” how faraway agents treat sentient beings in their part of the universe/multiverse.
ECL was introduced by Oesterheld in 2017 and his original paper continues to be the best (although lengthy) resource on the topic. It's a highly recommended read.
Introduction
The observable universe is large. Nonetheless, the full extent of the universe is likely much larger, perhaps infinitely so. This means that most of what’s out there is not causally connected to us. Even if we set out now from planet Earth, traveling at the speed of light, we would never reach most locations in the universe. One might assume that this means most of the universe is not our concern. In this post, we explain why all of the universe—and all of the multiverse, if it exists—may in fact concern us if we take something called evidential cooperation in large worlds (ECL) into account.[1] Given how high the stakes are, on account of how much universe/multiverse might be out there beyond our causal reach, ECL is potentially very important. In our view, ECL is a crucial consideration for the effective altruist project of doing the most good.
In the next section of this post, we explain the theory underlying ECL. Building on that, we outline how one might do ECL, in practice, and how doing ECL means (we claim) doing more good. We conclude by sharing some information on how you can get involved. We will also publish an FAQ in the near future [update: published!], which will address some possible objections to ECL.
The twin prisoners’ dilemma
Exact copies
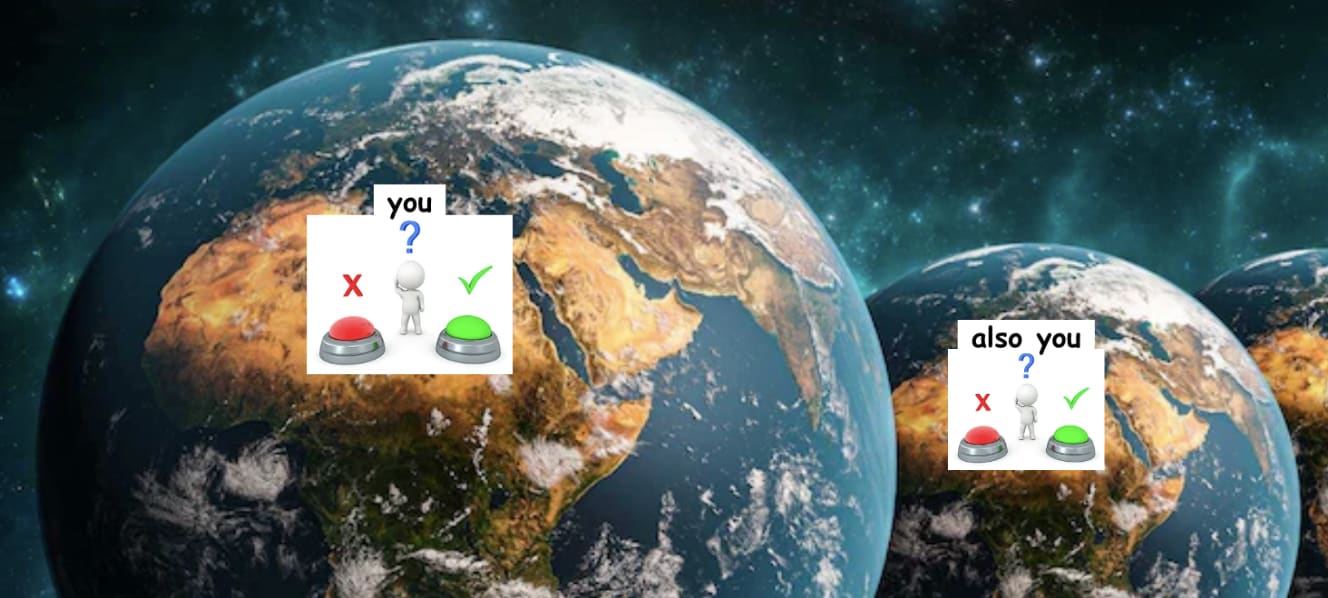
Suppose you are in a prisoner’s dilemma with an exact copy of yourself:
- You have a choice: You can either press the defect button, which increases your own payoff by $1, or you can press the cooperate button, which increases your copy’s payoff by $2.
- Your copy faces the same choice (i.e., the situation is symmetric).
- Both of you cannot see the other’s choice until after you have made your own choice. You and your copy will never interact with each other after this, and nobody else will ever observe what choices you both made.
- You only care about your own payoff, not the payoff of your copy.
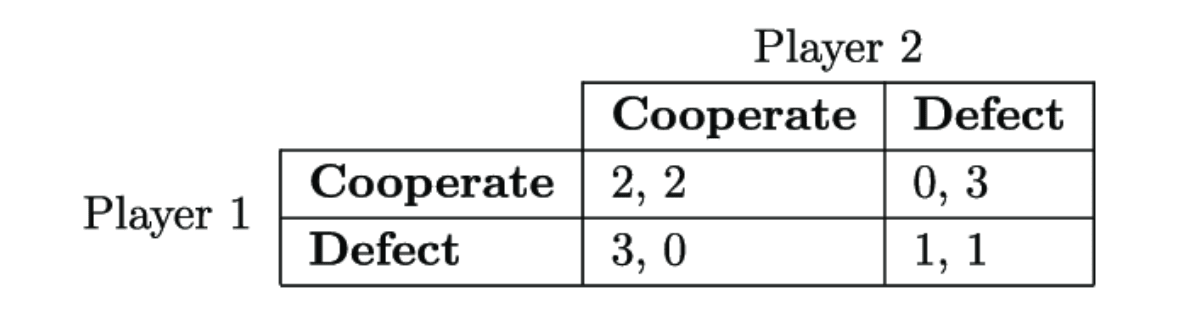
This situation can be represented with the following payoff matrix:
Looking at the matrix, you can see that regardless of whether your copy cooperates or defects, you are better off if you defect. “Defect” is the strictly dominant strategy. Therefore, under standard notions of rational decision making, you should defect. In particular, causal decision theory—read in the standard way—says to defect (Lewis, 1979).
However, the other player is an exact copy of yourself. In other words, you know that they will undergo the same decision-making process as you, and arrive at the same decision as you. If you cooperate, they cooperate. If you defect, they defect. You can see this even more clearly when considering two identical deterministic computer algorithms playing the prisoner’s dilemma against each other. You know that you both cooperating gives you a better payoff than you both defecting. Some theories, among them evidential decision theory and functional decision theory, therefore recommend cooperating in the twin prisoners’ dilemma. Throughout this post, we assume the perspective that cooperating against copies is rational, although you can find many alternative perspectives in the academic literature.
General case
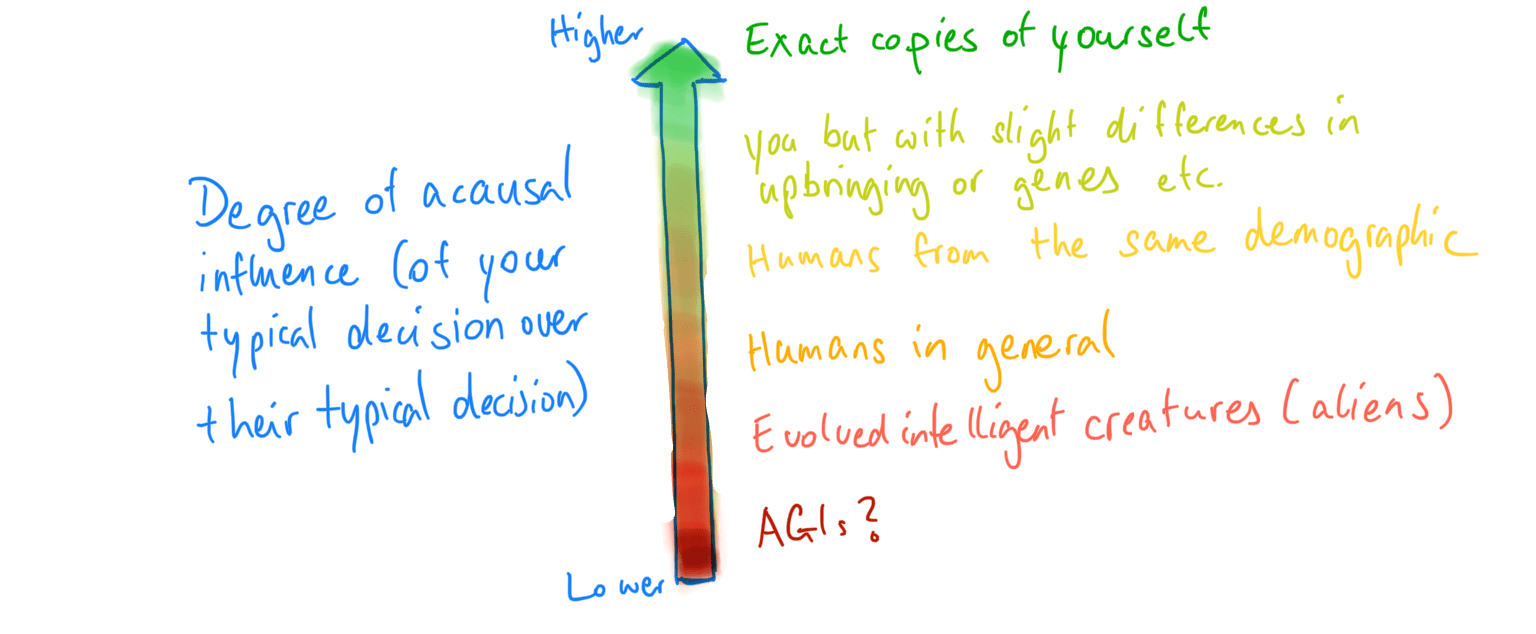
The argument for cooperation is most intuitive if you’re dealing with an exact copy of yourself. What if we instead consider:
- A (near-)copy who is the same as you, except that you and they are handed a pair of different-colored shoes before you both make your decisions.
- Your near-copy who was created a day ago, and put into an environment with mundane differences to yours.
- Your near-copy who was created a year ago, and put into a different environment.
- Your identical twin who had minor differences in upbringing.
- A randomly chosen human.
- A randomly chosen intelligent biological being (including aliens).
- A randomly chosen intelligent being (including artificial intelligences).
The first example, the near-copy who just has different-colored shoes, seems unlikely to follow an importantly different decision process from you regarding the twin prisoners’ dilemma. After all, they are identical to you except for one superficial aspect—the color of their shoes. Hence, while it’s not guaranteed, since you and they are not fully identical, you can expect, with high confidence, for them to cooperate if you cooperate and defect if you defect. Throughout this post, we assume the perspective that this gives you reason to cooperate.
We use the umbrella term acausal influence to refer to that which makes a near-copy more likely to cooperate with you in a prisoner’s dilemma when you cooperate.[2],[3],[4] Acausal influence is a property of particular decisions rather than agents.
As we move down through the list of examples above, it stands to reason that the relationship between your and the other agent’s decisions becomes less strong, because you and they become different in increasingly important ways. Your acausal influence over them is weaker.
Note that there are reasons to think that you can only leverage a small fraction of your total acausal influence on others. For more details, see appendix.
Why is this type of acausal cooperation important in practice? Introducing ECL
Our situation as a generalized twin prisoners’ dilemma-type situation
Evidential cooperation in large worlds (ECL) is the idea that it is possible for agents across the universe/multiverse to gain from acausal cooperation with each other, in a manner similar to that discussed in the previous section. We argue below that there are likely extremely many agents over whom we have some degree of acausal influence. Putting this together with the previous discussion, we arrive at the following key claim:
We plausibly want to adopt the following policy: Whenever we can benefit the values of relevant other agents in the multiverse—to a first approximation, agents that also engage in ECL[5]—more efficiently than we can benefit our own values, we should do so.[6] This is because everyone adopting this policy would make us better off. Hence, if we acausally influence many agents to adopt this policy and enough of these agents would otherwise do something worse from our perspective, then we are better off.
The main practical implication: it may be important to build AGI systems to be cooperative towards other value systems (insofar as we build AGI at all),[7] whether they are aligned or misaligned. Another way of framing this is that we want future earth-originating AI systems to be good citizens of acausal society. Doing so plausibly benefits many agents with values different from ours. So, even if we can’t tell exactly who else is engaging in ECL, or what their individual values are, this intervention has a good chance of benefiting them. Other agents engaging in acausal cooperation might do the same, or take another action that they expect to be broadly good for values different to theirs, and so some of these agents will aid our values.
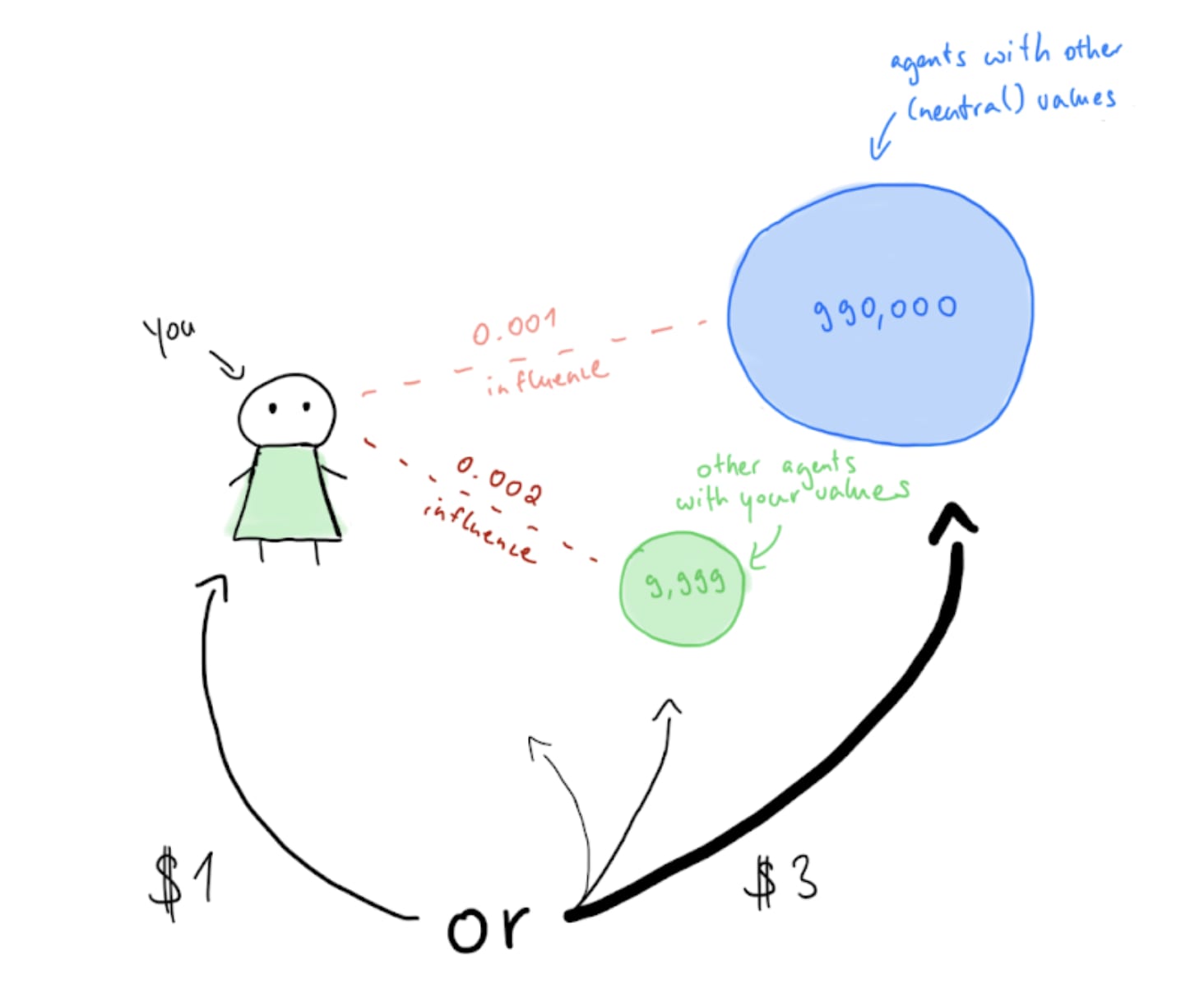
A toy model to quantitatively illustrate when cooperation is beneficial:
- Let’s say there are 1,000,000 agents.
- 10,000 (i.e., 1%) of these agents (including you) have the exact same values as you (e.g. utopia maximization), while 990,000 of the agents have values that are neutral from your perspective (e.g., paperclip maximization).
- Each agent faces the same decision and has exactly two choices:
- They can either generate an amount of what they value that’s equivalent to $1. This amounts to causally optimizing for their own values. Let’s call this choice “defect”.
- Or, they can generate value equivalent to $3 and evenly distribute that across all agents, including themselves. (That is, $3/1,000,000 worth of value per agent. For example, they would generate the equivalent of 2*$3/1,000,000 of paperclips if exactly two agents value paperclips.) Let’s call this choice “cooperate”.
- Your decision acausally increases the probability of everyone with the same values as you making the same decision by 0.002.
- Your decision acausally increases the probability of everyone with neutral values to you making the same decision by 0.001.
If you defect, you increase the expected money going towards your values by:
| $1 | (the money you take directly) |
| + $1*0.002*9,999 | (from the agents with your values that you acausally influence to also take $1) |
| ≈ $21 | (rounded to the nearest dollar) |
If you cooperate, you increase the expected money going towards your values by:
| $0.000003*10000 | (the amount of your $3 that you spend on your values) |
| + (9,999^2)*0.002*$0.000003 | (the amount agents with your values that you acausally influence to also distribute $3 spend on your values) |
| + 990,000*10,000*0.001*$0.000003 | (the amount agents with different values that you acausally influence to also distribute $3 spend on your values) |
| ≈ $30 | (rounded to the nearest dollar) |
Therefore, in this example, you should cooperate (for instance, by producing the jointly most efficient mix of utopia and paperclips). Note that almost all of the payoff you get from cooperating comes from acausally influencing agents with values different from yours towards cooperating. And most of the payoff from defecting comes from acausally influencing agents with your values towards defecting. However, the result is sensitive to the values you choose for the parameters. In this model, the most important factors, when it comes to deciding whether you should defect (i.e., causally optimize for our own values) or cooperate, are:
- High potential gains from cooperation favor cooperation. A high ratio of [value agents can provide to others when they cooperate] to [value they gain when defecting] is favorable to cooperation.
- Relatively high influence over agents who have different values to you favors cooperation. A high ratio of [acausal influence on agents with other values] to [acausal influence on agents with your values] is favorable to cooperation. This is because, while influencing agents with your values to cooperate hurts you (because instead of just optimizing for your values, they now put some some of their resources towards benefiting other values), influencing agents with different values to cooperate benefits you (because instead of just optimizing for their own values, they now put some of their resources towards benefiting your values).[8]
- Your absolute level of per-agent acausal influence stops mattering if the total population size is sufficiently large.[9] In particular, many people have the initial intuition that having only little acausal influence per agent favors defection. However, this is incorrect if the total population of agents you acausally influence is large. If the population is large, then virtually all effects of your action are acausal, regardless of whether you cooperate or defect: the total acausal effects of both defecting and cooperating increase linearly with the number of agents you influence, all else equal.[10],[11]
If you found out that all your acausal influences are in fact smaller (or larger) than you thought, this does not change the relative value of cooperation versus defection. What matters is the ratio of your acausal influence on agents with your values versus agents with different values.
The model presented here has some important limitations[12] and the conclusions vary slightly if you choose a different setup to model acausal cooperation. For example, depending on the model, a higher fraction of agents with your values either increases or decreases the relative value of cooperation. The general thrust stays the same across models, though: The more you acausally influence agents with different values from you, the more action-relevant ECL is.
Overall, this leaves us with the following conditions under which ECL is action-relevant (i.e., recommends us to cooperate when we would otherwise defect):
- There exist very many agents with different values to us.[13]
- We can acausally influence these agents toward trying to benefit our values by trying to benefit theirs.
- The benefit to our values that we get from influencing these other agents towards trying to benefit our values outweighs the cost. (The cost is us spending resources in our light cone on things other than the direct instantiation of what we value.)[14]
In the remainder of this post, we argue for each of these conditions. We also gradually relax the following assumptions from the above toy model:
- Every agent faces the same binary choice: “optimize purely for your own values” or “benefit agents with different values.”
- Every agent whose payoff we can increase can increase our payoff.
Some of the discussion in the appendix also relaxes the assumption that there are two distinct categories: “agents with our values” and “agents with different values.”
Many agents
In our example above, we had acausal influence over 999,999 agents. This section is concerned with the question: Are there, in fact, many agents out there to cooperate with?
Our universe (or multiverse) appears to be very large, perhaps infinitely so, which means that it likely contains very many—perhaps infinitely many—agents with whom we could potentially acausally cooperate. There are three main ways in which physicists believe the universe/multiverse could be large:[15]
- Spatio-temporal expanse. The universe is very plausibly spatially infinite.[16] If this is the case, then we expect there to be infinitely many civilizations. (This does open up issues of infinite ethics. See our FAQ for more.) If we condition on the universe being finite, on the other hand, it is still many times the size of the observable universe. This makes it plausible that there are many agents. However, estimates on the rarity of intelligent life vary widely, so it is far from guaranteed in the finite case that there are enough agents to justify ECL having strong implications.[17],[18]
- Inflationary multiverse. According to eternal inflation, a popular explanation of the early universe amongst cosmologists, our universe is just one bubble universe in an inflationary multiverse.
- Everett branches.[19] Under the Everett interpretation of quantum mechanics, also known as many-worlds,[20] there is an extremely large and growing number of parallel universes known as Everett branches. Some branches will be very similar to ours while some will be very different. If they exist, we can expect many of these branches to contain agents.[21] We can also expect to have acausal influence on many of these agents, since many of them are very similar to us. On the contrary, these similar agents might largely share our values anyway, making cooperation less useful.

Overall, we believe there is strong evidence for a large world, and thus many agents.[22] Additionally, even if one believes that the world likely does not contain enough agents to justify ECL, we have more (acausal) influence in the worlds that do contain many agents, and so our expected impact is higher if we focus on (the credence that we have in) those worlds.[23] Note that only one of the three ways we’ve presented need be true for the many agents premise to hold.[24] For more detail on the universe’s size, see our appendix.
Acausal influence on agents with other values
The toy example above assumes that we can acausally change the probability of agents with other values taking a decision that benefits us by 0.001. This section is concerned with the question: If we act cooperatively towards other agents, are they actually more likely to reciprocate?
We have already argued the basic case for considering acausal influence in our “Twin prisoners’ dilemma” section. The basic argument for thinking we can acausally influence agents with other values to benefit us is simple: We are faced with the decision of either trying to benefit other agents, or causally optimizing for our own values. Meanwhile, other agents face the same decision, and make decisions similarly to us. Because of this, our decision acausally influences them towards doing the same thing as us (i.e., benefiting other values, or causally optimizing for one’s own). Hence, if we try to benefit them, they will try to benefit us.
This argument has a few gaps:
- Why do we expect these agents to make decisions in a similar way to us?
- In reality, there are no actions neatly labeled “benefit others” or “optimize for yourself.” We just have a bunch of options for things we could do and other agents might have very different options. If I write an ECL explainer arguing that we should be more cooperative, and an agent in another part of the universe changes their AI training run to include more diverse perspectives on morality, this might be mutually beneficial, but it’s unclear to what extent we can be described as “two similar agents taking the same decision in similar situations.”
- Even if we try to benefit some agent, how do we know we are acausally influencing that agent to try to benefit exactly us? What if we benefit one agent who ends up benefiting a third agent?
To sketch an argument for why other agents might make decisions about ECL in a similar way to us: We think it’s likely that agents reason in ways that are somewhat convergent. Through a realist lens—i.e., assuming there is a unique way of reasoning that is objectively rational—one would expect reasoning to converge to what is “correct”. From an antirealist perspective, we expect some convergence to what “wins”—i.e., successful agents tend to reason in similarly effective ways. We expect reasoning that outputs “cooperate” in the twin prisoners’ dilemma, and which generalizes from there, to occur at some frequency. We further expect that some agents who reason in this way will think about the implications and discover something in the ballpark of ECL. This leads us to believe that we are able to acausally influence some agents’ ECL-inspired actions through our own ECL-inspired actions. Note that this line of reasoning is contested. A later section will touch on the potential fragility of acausal influence. (For adjacent work, see Finnveden, 2023.)
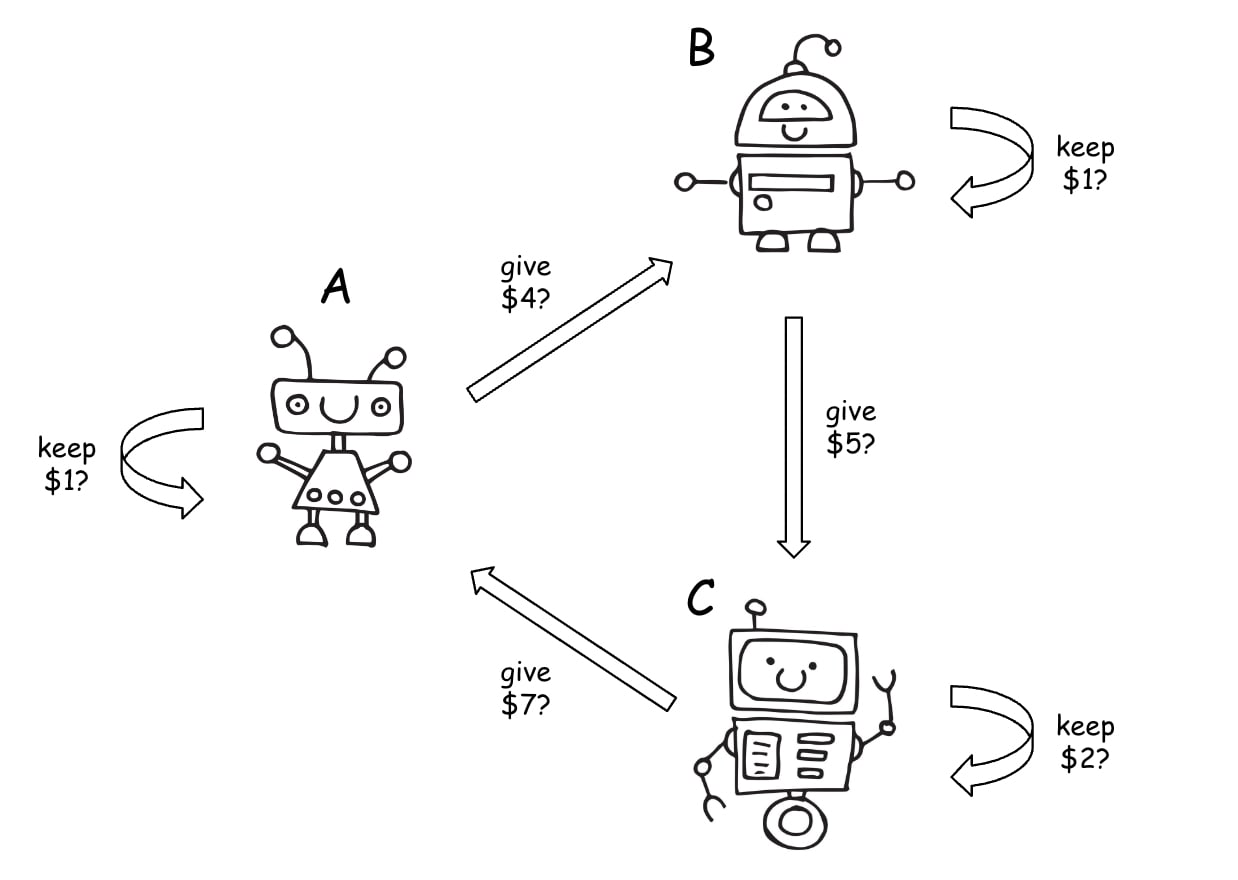
To address the latter two concerns (firstly, that different agents face different situations with no “cooperate” label; secondly, that there’s no guarantee other agents will benefit us specifically), we will look at a toy example in which agents face different decisions from each other, and cannot mutually benefit each other. We have three agents, A, B, and C:
- Agent A can get $1 by doing nothing, or increase agent B’s payoff by $4 by clapping her hands.
- Agent B can get $1 by doing nothing, or increase agent C’s payoff by $5 by whirring her antenna.
- Agent C can get $2 by doing nothing, or increase agent A’s payoff by $7 by stamping her wheel.
The agents have common knowledge of the situation and of having very similar decision-making processes to each other. (For instance, maybe they each know that all three of them are copies of GPT-N that received a nearly identical prompt, with the only difference in the prompt being the part where they are told which of the three agents they are.)
What should agent A do to maximize her payoff in this situation? We propose that she should reason as follows: “Instead of framing my decision as picking between doing nothing and clapping my hands, I can frame my decision as keeping money or giving money. I would do the same reframing if I were in the other agents’ position, so they are probably also framing their decision as keeping or giving money. I now find myself in the same position as agent C:
- Me not doing anything is keeping money, which is equivalent to agent C keeping money by not doing anything. Let’s call this action defecting.
- Me clapping my hands is giving money, which is equivalent to C giving money by stamping her wheel. Let’s call this action cooperating.
- I stand in the same relationship to C as C does to B. I know that C makes decisions similarly to me, and that C knows that they make decisions similarly to B.
- Hence, if I cooperate, C is likely to also cooperate. If I defect, C is likely to defect.
- Since I gain only $1 if I and C defect, and $7 if I and C cooperate, I should cooperate.”
The first thing we can see is that even in a situation where we cannot mutually affect each other’s payoffs, we can still acausally influence another agent towards trying to benefit us by trying to benefit some third agent ourselves. There can be cyclic arrangements like this with many more than three agents—the logic remains the same. We do not need to worry about finding the exact agent who can benefit us: If we generally benefit agents that are like us, we are more likely to be benefitted in turn. (For more on this, see Oesterheld, 2017, sec. 2.9.)
Secondly, acausal influence is not limited to situations where we have the exact same set of actions available as another agent. As in the three-agent example, we can apply the concept of reframing our decision to something more abstract such that many other agents can be said to face the same abstract decision as us. In particular, we can think of ourselves as facing one big abstract decision: Do we want to commit ourselves to acting cooperatively towards other agents who do ECL? If other agents frame things similarly, we and they find ourselves in similar situations. And if we both make such a commitment, it does not matter that the specifics of our downstream decisions look different. Therefore, even if the actions available to us humans are very different from the actions available to those we want to acausally cooperate with, we still have reason to believe that deciding to act cooperatively towards them will acausally influence them to act in kind. (For more on this, see Oesterheld, 2017, sec. 2.8.2. Oesterheld argues that agents who acausally cooperate should optimize for a compromise utility function. See also Finnveden, 2023.)[25]
Net gains from cooperation
The toy example assumes that we gain more if everyone cooperates than if everyone defects. This section is concerned with the following question: If we and the other agents cooperate, do we actually gain in expectation?
To answer this, we need to assess three important ingredients. Firstly, how much do we gain from one agent with other values benefitting us compared to our causal opportunity cost when we benefit them? This is the size of the potential gains from cooperation. In the initial prisoner’s dilemma we presented, the gains from cooperation would be represented in the payoff matrix. There are a few overlapping reasons for potentially high gains:[26] diminishing marginal returns within but not across light cones, comparative advantage, and combinability. These reasons mirror the reasons for why causal cooperation among humans is beneficial; we will not expand on them here. See our appendix for more.
Secondly, competence at cooperating. That is, how successful do we expect agents to be at benefiting each other? It is no use influencing others towards aiding you if they are incompetent at doing so. An important obstacle here is knowing what other agents value.[27] To figure out how good the average agent is at knowing how to benefit others, we can think about how good we are at this, and extrapolate. While it seems near-impossible for current humans to reason out the exact values of some alien civilization, we can make fairly confident broad guesses such as “agents who think about ECL tend to value having more rather than fewer resources, so they would prefer more opportunities for trade.” On this account, some ECL researchers strongly favor making future AI systems more cooperative. We think that much better educated guesses could be made in the future, after:
- gaining information, for example by encountering aliens in our light cone and extrapolating from them;
- becoming smarter, for example by developing advanced artificial intelligence; or
- by simply thinking more about known considerations—for example, we could think about which kinds of values evolution or gradient descent select for, or what types of agents will tend to have lots of resources and an interest in ECL-like trade.[28]
Overall, we expect that agents will be fairly competent at cooperating.
The third ingredient: the right kind of acausal influence. For ECL to recommend cooperation, it must be the case that our cooperation acausally influences agents to benefit us more than it influences agents to take actions that are worse for us. By and large, the acausal costs (benefits) of our actions will come from us acausally influencing agents with our (different) values to cooperate instead of defect. Note that we have already established that the absolute level of acausal influence we have over other agents does not matter if the population of agents is sufficiently large, so we can exclusively focus on the ratio of our respective acausal influences.
The size of this ratio is highly contested. We don’t take a stance in this document on what range of ratios is plausible. The personal view of one of the authors, Chi, is that we have enough acausal influence over agents with different values that the ratio is above the critical ratio. (Below which doing ECL would not be worth it.) This seems like a worthwhile topic of investigation and a large source of uncertainty about whether ECL is action-relevant. For more details, see the appendix.
Putting it all together
We have discussed the idea of acausal influence, and from there, how we might want to engage in multiverse-wide cooperation with aliens and distant AGIs. To conclude with something poetic, we excerpt from Richard Ngo’s recent reflection:
We’ve seen a [lot] of trends in the evolution of human values—e.g. they’ve become more individualistic, more cosmopolitan, and so on, over time. Imagine that trends like these are actually strong enough that, in the future, after studying psychology and sociology and other related topics very deeply, we realize that there were only ever a handful of realistic outcomes for what society’s values would look like once it spread to an intergalactic scale. As a toy example, imagine that the only two plausible attractors were:
- A society which prioritized individual happiness above all else—which meant that the people in it were often very solitary and disengaged from others around them.
- A society which prioritized meaningful relationships above all else—which meant that people often underwent significant suffering for the sake of love.
Imagine now that you’re running one of those societies. And you think to yourself: right now I’m only optimizing for people being happy, but I could easily optimize for people being happy and having meaningful relationships, in a way which wouldn’t reduce their happiness much. I’m not going to do it, because I care much more about happiness. But if I encountered the leader of a world that cared only about relationships, and they offered me a deal where we both spent 10% of our time optimizing for the others’ values, then that’d be a great deal for both of us.
How to get involved
Short-term research fellowships
There are a few different research programs that might be open towards ECL-inspired work, either conceptual or technical. Historically, these have been:
- The Center on Long-Term Risk’s Summer Research Fellowships.
- The Astra Fellowship (the first iteration of which was in early 2024); at least, the streams with Lukas Finnveden and Daniel Kokotajlo, and perhaps other streams.
- The Constellation Visiting Researcher Program. (The first iteration of which was likewise in early 2024.)
- The early 2024 MATS stream with Caspar Oesterheld.
We expect at least some of these programs to continue being open towards this kind of work, and for perhaps others to join the list.
Long-term employment
We don’t know of any organizations specifically focused on ECL. The only organizations we know of that have carried out some ECL research are the Center on Long-Term Risk (CLR), Open Philanthropy’s worldview investigations team, and a couple of individuals at FOCAL at Carnegie Mellon University. These organizations might be open to hiring more people to work on ECL in the future, although we are very unsure about how likely that is. The best bet might be CLR. Additionally, MIRI has done some decision theory research that is relevant to ECL, as have some academic institutions.
Reach out to Chi
I, Chi Nguyen, might be looking for ECL collaborators in the future. (Mostly for ML or conceptual research, but perhaps also for other projects, e.g., posts like this one or running events.) Get in touch with me (linhchismail [] gmail [] com) if you are potentially interested. I might also be able to connect you to others in ECL, recommend programs, or find other ways of helping you. If you do reach out, it would be helpful if your email includes one or two concrete questions, curiosities, objections, research angles, or details on the kinds of work or other opportunities you’d be open to. I probably won’t have much more useful to say than what is written here if you just say you are interested in ECL and wonder how to get involved. (Although maybe this will change at some point.)
Funding
In terms of funding, we encourage those interested in doing ECL research and/or upskilling to apply to the Long-Term Future Fund, the CLR Fund, Lightspeed Grants (if they run another round), or Manifund Regrants.
How to skill up to work on ECL
We expect it would not take long for someone with good personal fit to become a leading expert in ECL or one of its subtopics. Our best guess is that one can reach the frontier of ECL knowledge with around three months of skilling up half-time, starting from knowing ~nothing about ECL or decision theory. We list recommended readings below.
Recommended readings
Our number one recommendation is to read Oesterheld’s ‘Multiverse-wide cooperation via correlated decision making’ (2017: summary; full paper). This is ECL’s seminal work. (Bear in mind that the ‘Interventions’ section is now a little outdated, however.) The full paper is long,[29] but accordingly comprehensive.
For shorter, introductory-level material, we recommend:
- ‘Commenting on MSR, Part 1: Multiverse-wide cooperation in a nutshell’ (Gloor, 2017)
- ‘Multiverse-wide cooperation [EA Global talk]’ (Oesterheld, 2017)
- Though this talk offers little in addition to the post you are reading
- ‘Three reasons to cooperate’ (Christiano, 2022)
- This isn’t specifically about ECL, but mentions it and offers a helpful frame for thinking about it
For deep dives into various aspects of ECL theory, we recommend:
- ‘Asymmetric ECL’ (Finnveden, 2023)
- ‘When does EDT seek evidence about correlations?’ (Finnveden, 2023)
- ‘Asymmetric ECL with evidence’ (Finnveden, 2023)
- This post builds on the above two
- ‘Modeling Evidential Cooperation in Large Worlds’ (Treutlein, 2023)
For work on the potential implications of ECL, we recommend:
- ‘Implications of ECL’ (Finnveden, 2023)
- ‘How ECL changes the value of interventions that broadly benefit distant civilizations’ (Finnveden, 2023)
- ‘ECL with AI’ (Finnveden, 2023)
- Loosely builds on the post above
- ‘Can we benefit the values of distant AIs?’ (Finnveden, 2023)
- Builds on ‘Asymmetric ECL’ and loosely builds on ‘ECL with AI’
- ‘Are our choices analogous to AIs' choices?’ (Finnveden, 2023)
- Loosely builds on ‘Asymmetric ECL’, ‘ECL with AI’, and ‘Can we benefit the values of distant AIs?’
For more on the decision theory underlying ECL (all from the perspective of proponents of such decision theories), we recommend:
- Evidential Decision Theory (Ahmed, 2021)
- This is a short book that walks a reader through the fundamentals of evidential decision theory
- Evidence, Decision and Causality (Ahmed, 2014)
- This book is a deep dive into the shortcomings of causal decision theory and the merits of evidential decision theory
- There is a summary of this book on the EA Forum
- ‘Newcomb's Problem’ (Yudkowsky, 2016)
- This article describes Newcomb’s problem—the original thought experiment in the decision theory literature—and how causal, evidential, and logical decision theories answer this problem
- ‘Newcomb's Problem and Regret of Rationality’ (Yudkowsky, 2008)
- ‘Dilemmas for Superrational Thinkers, Leading up to a Luring Lottery’ (Hofstadter, 1985)
- ‘Extracting money from causal decision theorists’ (Oesterheld & Conitzer, 2021)
And for other commentary on ECL, we recommend:
- ‘Commenting on MSR, Part 2: Cooperation heuristics’ (Gloor, 2018)
- ‘Three wagers for multiverse-wide superrationality’ (Treutlein, 2018)
We’d like to be able to point to some critiques, as well, but unfortunately there aren’t any public critiques of ECL, as far as we can tell. This does not mean there aren’t valid potential critiques. Notably, there is a rich academic literature on decision theory, which includes arguments in favor of causal over non-causal decision theories.
For an alternative (albeit heavily overlapping) reading list by the Center on Long-Term Risk, see here.
Acknowledgements
We are grateful to Daniel Kokotajlo, Lukas Finnveden, Kit Harris, Euan McLean, Emery Cooper, Anthony DiGiovanni, Caspar Oesterheld, Vivek Hebbar, Tristan Cook, Sylvester Kollin, Jesse Clifton, and Nicolas Mace for helpful feedback on earlier versions of this post and other contributions. This does not imply endorsement of all, or any, claims in the post.
To finish off, a photo of our future intergalactic snack shop:

- ^
ECL was introduced in Caspar Oesterheld’s seminal paper “Multiverse-wide Cooperation via Correlated Decision Making”. (Note: “multiverse-wide cooperation” was the old name for ECL.)
- ^
We define acausal influence as a property of decision-making, rather than a property of agents.
- ^
i) Different people refer to non-causal relationships using different terms that describe partially different and partially overlapping concepts. Examples include “logical influence,” “logical correlation,” “correlation,” “quasi-causation,” “metacausation,” and “entanglement.” We use “acausal influence” as an umbrella term.
ii) Some readers may wonder how, if at all, acausal influence and ECL relate to acausal trade. We address this in our upcoming post: “ECL FAQ”.iii) For more arguments in favor of cooperation in the twin prisoners’ dilemma and other thought experiments, see, for example, Almond (2010a), Almond (2010b), and Ahmed (2014).
- ^
For example, evidential decision theory would say that conditioning on your own choice changes the probability that the other person will cooperate. The size of this change is the size of your acausal influence. In this definition, acausal influence is a property of particular decisions rather than agents, and not a binary, but comes in gradations. Whether you should cooperate with someone depends on how strongly you think your decision acausally influences theirs.
- ^
For now, we are assuming that everyone who is doing ECL is cooperating with everyone else who is doing ECL. The real picture is likely quite a lot more complicated but unfortunately out of scope for this document. A second toy model below hints at some of the considerations at play.
- ^
Notably, this policy would not involve causally optimizing for purely our own values.
- ^
For an attempt at quantifying this claim, see “How ECL changes the value of interventions that broadly benefit distant civilizations” (Finnveden, 2023).
- ^
Note that “high acausal influence” might trade off with “high potential gains from cooperation.” It seems plausible, for example, that misaligned artificial superintelligences have the most power to benefit us, but we can barely acausally influence them. Meanwhile, we might be able to acausally influence our close copies in other Everett branches by a lot, but they cannot benefit us as much because they have less power than an AGI and because their default action would already be quite beneficial to us (because they have similar values).
- ^
At smaller population levels, the direct gain you obtain by defecting (in the above example, $1) makes up a significant portion of your total gain ($21 in the defection case, in the above example). In these cases, your absolute acausal influence matters because it is pitched against your influence on yourself (which is exactly 1 since you perfectly influence your own action.)
- ^
In some other models you might get a non-linear scaling on the total acausal effects of cooperating.
- ^
We address Pascal’s mugging-type concerns about having very small acausal influence over a large number of agents in our FAQ. The tl;dr is that this situation is structurally quite different from a traditional Pascal’s mugging.
- ^
Most importantly:
- The model does not capture the fact that the total value you can provide to the commons likely scales with the diversity (and by proxy, fraction) of agents that have different values. In some models, this effect is strong enough to flip whether a larger fraction of agents with your values favors cooperating or defecting.
- The model does not capture that your correlation with other agents only holds if their situation is similar enough to yours. For example, if there is a group of agents who are a very small fraction of the total population, mutual cooperation is not beneficial to them and they are better off always defecting. That is because, in our model, how much a value system benefits from others cooperating scales with how many agents have that value system. However, our model cannot capture this dynamic and always assumes that us cooperating increases the chance that others also cooperate.
- In this model, once there are sufficiently many agents with your values, cooperating also becomes the causally best action. That is because you split $3 across all agents when you cooperate: Hence, in the extreme where all agents have your values, you gain $3 for you value system by cooperating and only $1 by defecting. This is a good model for some situations and not for others.
- ^
We are assuming that you cannot take any action that directly increases the payoff of agents with your values that is better than what you would do in the absence of these agents existing. In other words, if there are many agents we have acausal influence over but they all have the exact same values as us, then we should just act as we would if they did not exist.
- ^
Agents with other values also have to think they benefit more from trying to acausally influence us compared to causally optimizing for their own values. Otherwise, there is no reason for them to participate in this cooperation.
- ^
The ways we list correspond to three of the four levels in Tegmark (2009)’s multiverse hierarchy. They are also three of Greene (2011)’s nine types of multiverses: quilted, inflationary, and quantum, respectively. There are further theories, such as cyclic cosmology—another of Greene’s nine types, which also indicate that the universe/multiverse could be infinite (or at least very large), but we limit our discussion in the main text to theories that we consider to be most likely based on our understanding of what most cosmologists believe.
- ^
The two priors in footnote 6 of Vardanyan, Trotta and Silk (2011) lead to 98.6% and 46.2% posterior probabilities, respectively, of the universe being exactly flat (and therefore infinite, with infinitely many aliens).
(Note: I—Will—think that these Vardanyan et al. results are contentious. (I’m still quoting them, though, because there appears to be a dearth of papers on the topic of assigning credences to the possible shapes and sizes of our universe.) To the best of my knowledge, based on conversation, cosmologists can be roughly divided into two clusters: those who don’t subscribe to eternal inflation, and those who do. Of those who don’t, many (most?) seem to have a uniform prior over the cosmic density parameter. Under this prior, the probability that the universe is exactly flat is zero.* Meanwhile, those who do subscribe to eternal inflation believe that our universe is negatively curved and therefore infinite, on account of details in the equations that describe how bubble/pocket universes arise (Guth, 2013). (However, this second camp also believes that there are infinitely many universes, so believing that our universe is negatively curved and therefore infinite, and believing that we live in an infinite multiverse, are not independent beliefs.)
*Nonetheless, the contention with Vardanyan et al. in this case doesn’t have much effect on the likelihood that the universe is spatially infinite. The universe is measured to be almost exactly flat: to a first approximation, under a uniform prior and ignoring anthropic considerations, this gives us 50% probability that the universe is positively curved and therefore finite, and 50% probability that the universe is negatively curved and therefore infinite.)
- ^
Reasoning about the frequency of civilizations is difficult. Attempts include the Drake equation (and the Drake equation reworked with distributions rather than point estimates—Sandberg, Drexler and Ord, 2018) and Robin Hanson’s grabby aliens model.
- ^
In fact, the authors of this post disagree about how likely a finite, purely spatio-temporal universe would be to contain enough agents to justify ECL.
- ^
Everett branches and the eternal multiverse are speculatively united under the cosmological interpretation of quantum mechanics (Aguirre & Tegmark, 2011). This position does face opposition, for example, from Siegel (2023). (Note: Aguirre and Tegmark use their own terminology, using “Universe” with a capital U to refer to what most other people refer to as the multiverse.)
- ^
One of the authors, Will, endorses the viewpoint Sean Carroll puts forward in his 2019 book Something Deeply Hidden that “interpretation” is a misnomer. Copenhagen, and many-worlds, and hidden variables are not different interpretations of the same theory: they describe reality working in different ways; they are different theories. The other side of the argument would say that what makes a theory is whether it makes testable predictions. I, and Carroll and some others, I believe, would rebut, saying that what matters is what is real, and that on-paper reasoning as well as experimental verification should influence what one believes is real. In the quantum case specifically, I would also say that hidden variables has arguably been eliminated by Bell’s theorem experiments (e.g., Brubaker, 2021).
- ^
There is debate about whether, as the number of branches grows, the total amount of “stuff”—for want of a better word—grows with the number of branches, or whether it remains fixed, with each branch becoming an ever thinner slice of the total. This difference might be important in some ways. Nonetheless, this is not a relevant difference for ECL. Whether the total amount of stuff increases or not, the share of branches that we inhabit decreases in the same way as splittings occur; there is no difference in how we relate to the agents in other branches insofar as ECL is concerned. For more on the branching debate, see David Wallace’s 80,000 Hours podcast episode and/or mentions of “reality fluid” on LessWrong.
- ^
Even if this were not the case, we would be happy to wager on the possibility of extremely many agents in an expected value-style manner since the probability for extremely many agents surely is not Pascalian.
- ^
Unless you believe it is extremely unlikely that there are many agents. However, given modern cosmology, such a belief seems unjustified.
- ^
In addition to cosmology-based reasoning and evidence for believing there might be very many agents in our world, there is also Nick Bostrom’s presumptuous philosopher argument (pp. 9-10): given the fact that you exist, you should, all else equal, favor hypotheses which say that the world contains many observers (i.e., agents) over hypotheses which say there are few observers. However, the presumptuous philosopher relies on the self indicating assumption (SIA) for making anthropic updates, which is controversial and has problems when combined with evidential decision theory. The presumptuous philosopher was also originally designed as a counterargument to SIA (in the way that its conclusion, driven by SIA, arguably proves too much).
- ^
In principle, there is not even anything that limits our acausal influence to other agents’ actions. Having acausal influence simply means, “If I take action x, something else (whether that’s an action or other event) is made more likely even though I am not causally affecting it.” Although for our purposes, we usually only care about the ways in which our actions acausally influence other agents’ actions.
- ^
Assuming agents care about what happens in other light cones at all.
- ^
You might think it is of no concern to us whether we fail at predicting other agents’ values: Even if we fail to benefit other values, as long as they successfully benefit ours, we are happy. However, if we predictably fail at benefiting others, they have no reason to want to cooperate with us! In fact, if we employ a lopsided policy of “only cooperate if they know how to benefit us,” they are more likely to do the same. From the perspective of not yet knowing who will successfully figure out who can successfully benefit whom, it is better to employ the strategy “cooperate if agents on average know enough about what is beneficial to the other to make cooperation worthwhile for the other,” to make it more likely that everyone else adopts this strategy.
- ^
Oesterheld (2017, sec. 3.4) and Ngo (2023) discuss the latter point. In short, these agents’ values are very likely correlated with genetic fitness and beyond-the-light-cone thinking. Therefore, agents that engage in ECL seem more likely to care about happiness and suffering than about highly Earth-specific issues such as the value of the traditional family. So, we might want to weigh light cone-agnostic values more heavily than we otherwise would.
These claims about values are weakened by considering misaligned AIs. We expect the distribution of misaligned AI values, relative to the distribution of biological civilizations’ values or aligned AI values, to be closer to uniform over all values. For more on this, see Aldred (2023). (I—Will Aldred—do not think this consideration is original to me, but I could not find it written up elsewhere.)
- ^
Its core concepts were covered in this post, though, so reading the paper should take less time if you’ve already read this post.

Thanks for the post, Chi and Will. Somewhat relatedly, I liked Veritasium video on What Game Theory Reveals About Life, The Universe, and Everything.
I do not think there is any empirical evidence for this. We can only measure finite quantities, so any measurement we make would be perfectly compatible with a large finite universe. In other words, empirical evidence can update one towards a larger universe, but not from a finite to an infinite one. So my understanding is that claims about the universe being infinite rest entirely on having a prior with some probability mass on this possibility.
Note the universe is measured to be almost exactly flat locally. If I am looking into a straight railway track which extends a few kilometers in my field of view, it would maybe not be reasonable for me to conclude it is infite in expectation. A reasonable probability density function (PDF) for its length would decay sufficiently fast to 0 as the length increases, such that the expected length is still finite. Similarly, even though the universe looks flat locally (like the Earth does in some places, even though it is not), I feel like it would be reasonable to have a PDF describing its size which decays to 0 as the size increases. The tail of the PDF would have to decay faster than the squared size for the expected size to be finite[1].
The mean of a Pareto distribution would be infinite otherwise.
Hi Vasco, I’m having trouble parsing your comment. For example, if the universe’s large-scale curvature is exactly zero (and the universe is simply connected), then by definition it’s infinite, and I’m confused as to why you think it could still be finite (if this is what you’re saying; apologies if I’m misinterpreting you).
I’m not sure what kind of a background you already have in this domain, but if you’re interested in reading more, I’d recommend first going to the “Shape of the universe” Wikipedia page, and then, depending on your mileage, lectures 10–13 of Alan Guth’s introductory cosmology lecture series.
Thanks for following up, Will!
I agree. However, my understanding is that it is impossible to get empirical evidence supporting exactly zero curvature, because all measurements have finite sensitivity. I guess the same applies to the question of whether the universe is simply connected. In general, I assume zeros and infinities do not exist in the real world, even though they are useful in maths and physics to think about limiting processes.
Thanks for the links. I had skimmed that Wikipedia page.
Thanks for replying, I think I now understand your position a bit better. Okay, so if your concern is around measurements only being finitely precise, then my exactly-zero example is not a great one, because I agree that it’s impossible to measure the universe as being exactly flat.
Maybe a better example: if the universe’s large-scale curvature is either zero or negative, then it necessarily follows that it’s infinite.
—(I didn’t give this example originally because of the somewhat annoying caveats one needs to add. Firstly, in the flat case, that the universe has to be simply connected. And then in the negatively curved case, that our universe isn’t one of the unusual, finite types of hyperbolic 3-manifold given by Mostow’s rigidity theorem in pure math. (As far as I’m aware, all cosmologists believe that if the universe is negatively curved, then it’s infinite.))—
I think this new example might address your concern? Because even though measurements are only finitely precise, and contain uncertainty, you can still be ~100% confident that the universe is negatively curved based on measurement. (To be clear, the actual measurements we have at present don’t point to this conclusion. But in theory one could obtain measurements to justify this kind of confidence.)
(For what it’s worth, I personally have high credence in eternal inflation, which posits that there are infinitely many bubble/pocket universes, and that each pocket universe is negatively curved—very slightly—and infinitely large. (The latter on account of details in the equations.))
Thanks for elaborating!
I agree it makes sense to have some probability mass on the universe having null or negative local curvature. However, I think there is no empirical evidence supporting a null or negative global curvature:
Wikipedia's page seems to be in agreement with my 2nd point (emphasis mine):
I guess cosmologists may want to assume the properties of the observable universe match those of the entire universe in agreement with the cosmological principle. However, this has only proved to be useful to make predictions in the observable universe, so extending it to the entire universe would not be empirically justifiable. As a result, I get the impression the hypothesis of an infinite universe is not falsifiable, such that it cannot meaningly be true or false.
Useful so far! The problem of induction applies to all of our predictions based on past observations. Everything could be totally different in the future. Why think the laws of physics or observations will be similar tomorrow, but very different outside our observable universe? It seems like essentially the same problem to me.
Why then assume it's finite rather than infinite or possibly either?
What if you're in a short-lived simulation that started 1 second ago and will end in 1 second, and all of your memories are constructed? It's also unfalsifiable that you aren't. So, the common sense view is not meaningfully true or false, either.
Thanks for jumping in, Michael!
I agree it is essentially the same problem. I would think about it as follows:
Sorry for the lack of claririty. I did not mean to argue for a finite universe. I like to assume it is finite for simplicity, in the same way that it is practical to have physical laws with zeros even though all measurements have finite precision. However, I do not think there will ever be evidence for/against the entire universe being finite/infinite.
Hmm, okay, so it sounds like you’re arguing that even if we measure the curvature of our observable universe to be negative, it could still be the case that the overall universe is positively curved and therefore finite? But surely your argument should be symmetric, such that you should also believe that if we measure the curvature of our observable universe to be positive, it could still be the case that the overall universe is negatively curved and thus infinite?
My answer to both questions would be yes. In other words, whether the entire universe is finite or infinite is not a meaningful question to ask because we will never be able to gather empirical evidence to study it.