
Will Howard🔹
Bio
I'm a software engineer on the CEA Online team, mostly working on the EA Forum.
You can contact me at will.howard@centreforeffectivealtruism.org
Posts 18
Comments148
Topic contributions48
I haven't yet read the sequence, but I have it on my backlog to read based on finding your older post about this very interesting. I agree-voted "An FAQ about various objections" because I think the other two can be looked up/skimmed from the existing content, whereas I'm actually unfamiliar with the objections so that would be new info to me.
@Jeff Kaufman 🔸 it would be possible, we're currently using a library that claims to use heuristics based on the user's timezone and locale, but this doesn't seem to work very well. For the forum we use IP geolocation which is more reliable, so we can switch to that.
@Ian Turner unfortunately we do get some value out of non-GDPR-compatible analytics, and we want to try and optimise the site as a top-of-funnel intro to EA over time, so we think the banner is worth it for now.
Mini Forum update: Draft comments, and polls in comments
Draft comments
You can now save comments as permanent drafts:
After saving, the draft will appear for you to edit:
1. In-place if it's a reply to another comment (as above)
2. In a "Draft comments" section under the comment box on the post
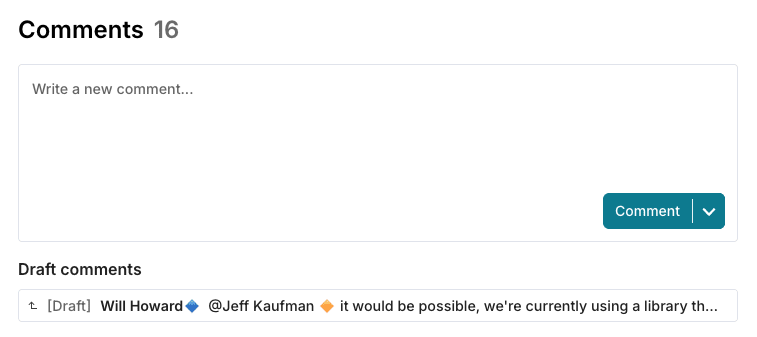
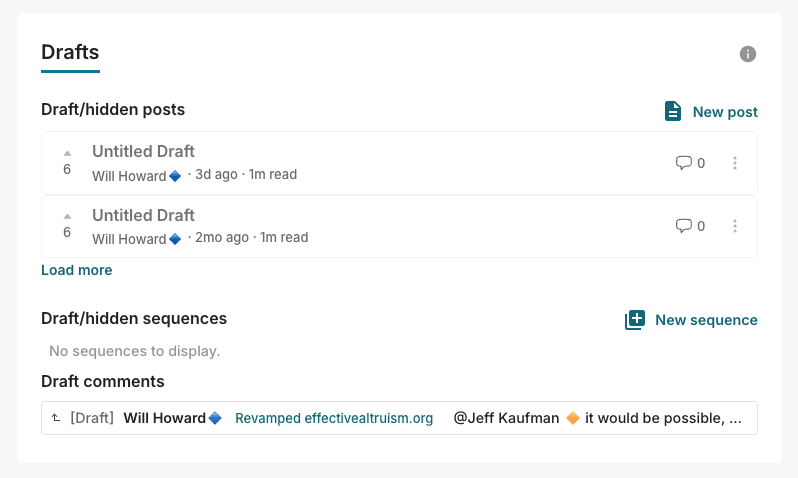
3. In the drafts section of your profile
The reasons we think this will be useful:
- For writing long, substantive comments (and quick takes!). We think these are the some of the most valuable comments on the forum, and want to encourage more of them
- For starting a comment on mobile and then later continuing on desktop
- To lower the barrier to starting writing a comment, since you know you can always throw it in drafts and then never look at it again
Polls in comments
We recently added the ability to put polls in posts, and this was fairly well received, so we're adding it to comments (... and quick takes!) as well.
You can add a poll from the toolbar, you just need to highlight a bit of text to make the toolbar appear:

And the poll will look like this...









Hey, I just spot checked a few posts throughout the handbook and found that all of them have audio now 😌. Is there anywhere left in the handbook where audio is missing for you? I can coordinate with Type III to get them filled in if so (though I'm not sure if the missing audio you were seeing was a problem on their end or our end)