by Max Daniel & Benjamin Todd
[ETA: See also this summary of our findings + potential lessons by Ben for the 80k blog.]
Some people seem to achieve orders of magnitudes more than others in the same job. For instance, among companies funded by Y Combinator the top 0.5% account for more than ⅔ of the total market value; and among successful bestseller authors, the top 1% stay on the New York Times bestseller list more than 25 times longer than the median author in that group.
This is a striking and often unappreciated fact, but raises many questions. How many jobs have these huge differences in achievements? More importantly, why can achievements differ so much, and can we identify future top performers in advance? Are some people much more talented? Have they spent more time practicing key skills? Did they have more supportive environments, or start with more resources? Or did the top performers just get lucky?
More precisely, when recruiting, for instance, we’d want to know the following: when predicting the future performance of different people in a given job, what does the distribution of predicted (‘ex-ante’) performance look like?
This is an important question for EA community building and hiring. For instance, if it’s possible to identify people who will be able to have a particularly large positive impact on the world ahead of time, we’d likely want to take a more targeted approach to outreach.
More concretely, we may be interested in two different ways in which we could encounter large performance differences:
- If we look at a random person, by how much should we expect their performance to differ from the average?
- What share of total output should we expect to come from the small fraction of people we’re most optimistic about (say, the top 1% or top 0.1%) – that is, how heavy-tailed is the distribution of ex-ante performance?
(See this appendix for how these two notions differ from each other.)
Depending on the decision we’re facing we might be more interested in one or the other. Here we mostly focused on the second question, i.e., on how heavy the tails are.
This post contains our findings from a shallow literature review and theoretical arguments. Max was the lead author, building on some initial work by Ben, who also provided several rounds of comments.
You can see a short summary of our findings below.
We expect this post to be useful for:
- (Primarily:) Junior EA researchers who want to do further research in this area. See in particular the section on Further research.
- (Secondarily:) EA decision-makers who want to get a rough sense of what we do and don’t know about predicting performance. See in particular this summary and the bolded parts in our section on Findings.
- We weren’t maximally diligent with double-checking our spreadsheets etc.; if you wanted to rely heavily on a specific number we give, you might want to do additional vetting.
To determine the distribution of predicted performance, we proceed in two steps:
- We start with how ex-post performance is distributed. That is, how much did the performance of different people vary when we look back at completed tasks? On these questions, we’ll review empirical evidence on both typical jobs and expert performance (e.g. research).
- Then we ask how ex-ante performance is distributed. That is, when we employ our best methods to predict future performance by different people, how will these predictions vary? On these questions, we review empirical evidence on measurable factors correlating with performance as well as the implications of theoretical considerations on which kinds of processes will generate different types of distributions.
Here we adopt a very loose conception of performance that includes both short-term (e.g. sales made on one day) and long-term achievements (e.g. citations over a whole career). We also allow for performance metrics to be influenced by things beyond the performer’s control.
Our overall bottom lines are:
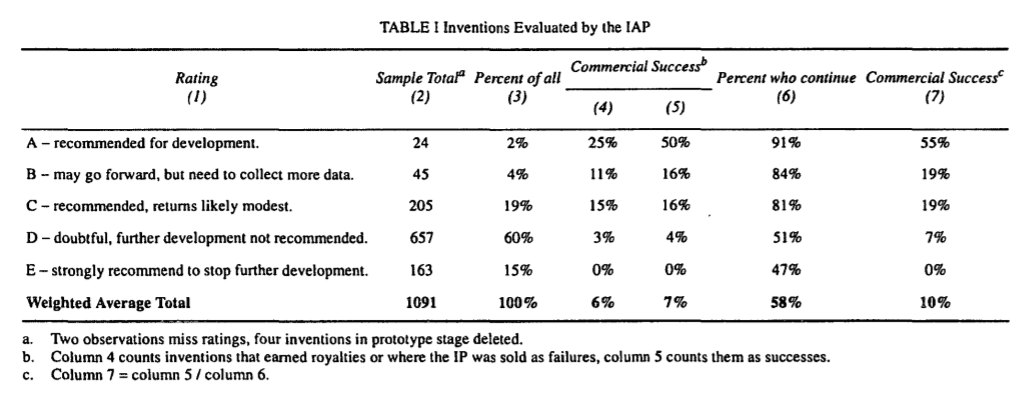
- Ex-post performance appears ‘heavy-tailed’ in many relevant domains, but with very large differences in how heavy-tailed: the top 1% account for between 4% to over 80% of the total. For instance, we find ‘heavy-tailed’ distributions (e.g. log-normal, power law) of scientific citations, startup valuations, income, and media sales. By contrast, a large meta-analysis reports ‘thin-tailed’ (Gaussian) distributions for ex-post performance in less complex jobs such as cook or mail carrier[1]: the top 1% account for 3-3.7% of the total. These figures illustrate that the difference between ‘thin-tailed’ and ‘heavy-tailed’ distributions can be modest in the range that matters in practice, while differences between ‘heavy-tailed’ distributions can be massive. (More.)
- Ex-ante performance is heavy-tailed in at least one relevant domain: science. More precisely, future citations as well as awards (e.g. Nobel Prize) are predicted by past citations in a range of disciplines, and in mathematics by scores at the International Maths Olympiad. (More.)
- More broadly, there are known, measurable correlates of performance in many domains (e.g. general mental ability). Several of them appear to remain valid in the tails. (More.)
- However, these correlations by itself don’t tell us much about the shape of the ex-ante performance distribution: in particular, they would be consistent with either thin-tailed or heavy-tailed ex-ante performance. (More.)
- Uncertainty should move us toward acting as if ex-ante performance was heavy-tailed – because if you have some credence in it being heavy-tailed, it’s heavy-tailed in expectation – but not all the way, and less so the smaller our credence in heavy-tails. (More.)
- To infer the shape of the ex-ante performance distribution, it would be more useful to have a mechanistic understanding of the process generating performance, but such fine-grained causal theories of performance are rarely available. (More.)
- Nevertheless, our best guess is that moderately to extremely heavy-tailed ex-ante performance is widespread at least for ‘complex’ and ‘scaleable’ tasks. (I.e. ones where the performance metric can in practice range over many orders of magnitude and isn’t artificially truncated.) This is based on our best guess at the causal processes that generate performance combined with the empirical data we’ve seen. However, we think this is debatable rather than conclusively established by the literature we reviewed. (More.)
- There are several opportunities for valuable further research. (More.)
Overall, doing this investigation probably made us a little less confident that highly heavy-tailed distributions of ex-ante performance are widespread, and we think that common arguments for it are often too quick. That said, we still think there are often large differences in performance (e.g. some software engineers have 10-times the output of others[2]), these are somewhat predictable, and it’s often reasonable to act on the assumption that the ex-ante distribution is heavy-tailed in many relevant domains (broadly, when dealing with something like ‘expert’ performance as opposed to ‘typical’ jobs).
Some advice for how to work with these concepts in practice:
- In practice, don’t treat ‘heavy-tailed’ as a binary property. Instead, ask how heavy the tails of some quantity of interest are, for instance by identifying the frequency of outliers you’re interested in (e.g. top 1%, top 0.1%, …) and comparing them to the median or looking at their share of the total.[3]
- Carefully choose the underlying population and the metric for performance, in a way that’s tailored to the purpose of your analysis. In particular, be mindful of whether you’re looking at the full distribution or some tail (e.g. wealth of all citizens vs. wealth of billionaires).
In an appendix, we provide more detail on some background considerations:
- The conceptual difference between ‘high variance’ and ‘heavy tails’: Neither property implies the other. Both mean that unusually good opportunities are much better than typical ones. However, only heavy tails imply that outliers account for a large share of the total, and that naive extrapolation underestimates the size of future outliers. (More.)
- We can often distinguish heavy-tailed from light-tailed data by eyeballing (e.g. in a log-log plot), but it’s hard to empirically distinguish different heavy-tailed distributions from one another (e.g. log-normal vs. power laws). When extrapolating beyond the range of observed data, we advise to proceed with caution and to not take the specific distributions reported in papers at face value. (More.)
- There is a small number of papers in industrial-organizational psychology on the specific question whether performance in typical jobs is normally distributed or heavy-tailed. However, we don’t give much weight to these papers because their broad high-level conclusion (“it depends”) is obvious but we have doubts about the statistical methods behind their more specific claims. (More.)
- We also quote (in more detail than in the main text) the results from a meta-analysis of predictors of salary, promotions, and career satisfaction. (More.)
- We provide a technical discussion of how our metrics for heavy-tailedness are affected by the ‘cutoff’ value at which the tail starts. (More.)
Finally, we provide a glossary of the key terms we use, such as performance or heavy-tailed.
For more details, see our full write-up.
Acknowledgments
We'd like to thank Owen Cotton-Barratt and Denise Melchin for helpful comments on earlier drafts of our write-up, as well as Aaron Gertler for advice on how to best post this piece on the Forum.
Most of Max's work on this project was done while he was part of the Research Scholars Programme (RSP) at FHI, and he's grateful to the RSP management and FHI operations teams for keeping FHI/RSP running, and to Hamish Hobbs and Nora Ammann for support with productivity and accountability.
We're also grateful to Balsa Delibasic for compiling and formatting the reference list.
[2] Similarly, don’t treat ‘heavy-tailed’ as an asymptotic property – i.e. one that by definition need only hold for values above some arbitrarily large value. Instead, consider the range of values that matter in practice. For instance, a distribution that exhibits heavy tails only for values greater than 10^100 would be heavy-tailed in the asymptotic sense. But for e.g. income in USD values like 10^100 would never show up in practice – if your distribution is supposed to correspond to income in USD you’d only be interested in a much smaller range, say up to 10^10. Note that this advice is in contrast to the standard definition of ‘heavy-tailed’ in mathematical contexts, where it usually is defined as an asymptotic property. Relatedly, a distribution that only takes values in some finite range – e.g. between 0 and 10 billion – is never heavy-tailed in the mathematical-asymptotic sense, but it may well be in the “practical” sense (where you anyway cannot empirically distinguish between a distribution that can take arbitrarily large values and one that is “cut off” beyond some very large maximum).
- ^
For performance in “high-complexity” jobs such as attorney or physician, that meta-analysis (Hunter et al. 1990) reports a coefficient of variation that’s about 1.5x as large as for ‘medium-complexity' jobs. Unfortunately, we can’t calculate how heavy-tailed the performance distribution for high-complexity jobs is: for this we would need to stipulate a particular type of distribution (e.g. normal, log-normal), but Hunter et al. only report that the distribution does not appear to be normal (unlike for the low- and medium-complexity cases).
- ^
Claims about a 10x output gap between the best and average programmers are very common, as evident from a Google search for ‘10x developer’. In terms of value rather than quantity of output, the WSJ has reported a Google executive claiming a 300x difference. For a discussion of such claims see, for instance, this blog post by Georgia Institute of Technology professor Mark Guzdial. Similarly, slide 37 of this version of Netflix's influential 'culture deck' claims (without source) that "In creative/inventive work, the best are 10x better than the average".
- ^
Similarly, don’t treat ‘heavy-tailed’ as an asymptotic property – i.e. one that by definition need only hold for values above some arbitrarily large value. Instead, consider the range of values that matter in practice. For instance, a distribution that exhibits heavy tails only for values greater than 10^100 would be heavy-tailed in the asymptotic sense. But for e.g. income in USD values like 10^100 would never show up in practice – if your distribution is supposed to correspond to income in USD you’d only be interested in a much smaller range, say up to 10^10. Note that this advice is in contrast to the standard definition of ‘heavy-tailed’ in mathematical contexts, where it usually is defined as an asymptotic property. Relatedly, a distribution that only takes values in some finite range – e.g. between 0 and 10 billion – is never heavy-tailed in the mathematical-asymptotic sense, but it may well be in the “practical” sense (where you anyway cannot empirically distinguish between a distribution that can take arbitrarily large values and one that is “cut off” beyond some very large maximum).

Great post! Seems like the predictability questions is impt given how much power laws surface in discussion of EA stuff.
I want to argue that things which look like predicting future citations from past citations are at least partially "uninteresting" in their predictability, in a certain important sense.
(I think this is related to other comments, and have not read your google doc, so apologies if I'm restating. But I think its worth drawing out this distinction)
In many cases I can think of wanting good ex-ante prediction of heavy-tailed outcomes, I want to make these predictions about a collection which is in an "early stage". For example, I might want to predict which EAs will be successful academics, or which of 10 startups seed rounds I should invest in.
Having better predictive performance at earlier stages gives you a massive multiplier in heavy-tailed domains: investing in a Series C is dramatically more expensive than a seed investment.
Given this, I would really love to have a function which takes in the intrinsic characteristics of an object, and outputs a good prediction of performance.
Citations are not intrinsic characteristics.
When someone is choosing who to cite, they look at - among other things- how many citations they have. All else equal, a paper/author with more citations will get cited more than a paper with less citations. Given the limited attention span of academics (myself as case in point) the more highly cited paper will tend to get cited even if the alternative paper is objectively better.
(Ed Boyden at MIT has this idea of "hidden gems" in the literature which are extremely undercited papers with great ideas: I believe the original idea for PCR, a molecular bio technique, had been languishing for at least 5 years with very little attention before later rediscover. This is evidence for the failure of citations to track quality.)
Domains in which "the rich get richer" are known to follow heavy-tailed distributions (with an extra condition or two) by this story of preferential attachment.
In domains dominated by this effect we can predict ex-ante that the earliest settlers in a given "niche" are most likely to end up dominating the upper tail of the power law. But if the niche is empty, and we are asked to predict which of a set would be able to set up shop in the niche--based on intrinsic characteristics--we should be more skeptical of our predictive ability, it seems to me.
Besides citations, I'd argue that many/most other prestige-driven enterprises have at least a non-negligible component of their variance explained by preferential attachment. I don't think it's a coincidence that the oldest Universities in a geography also seem to be more prestigious, for example. This dynamic is also present in links on the interwebs and lots of other interesting places.
I'm currently most interested in how predictable heavy-tailed outcomes are before you have seen the citation-count analogue, because it seems like a lot of potentially valuable EA work is in niches which don't exist yet.
That doesn't mean the other type of predictability is useless, though. It seems like maybe on the margin we should actually be happier defaulting to making a bet on whichever option has accumulated the most "citations" to date instead of trusting our judgement of the intrinsic characteristics.
Anyhoo- thanks again for looking into this!
Yeah this is great; I think Ed probably called them sleeping beauties and I was just misremembering :)
Thanks for the references!