Disclaimer: We (Sam Nolan, Hannah Rokebrand and Tanae Rao) do not represent GiveWell, or any of the organisations we mention. All opinions and errors are our own. This notebook is a part of a submission GiveWell's Change Our Mind Contest.
Work Done: This is about 300 hours of work done between Sam Nolan, Hannah Rokebrand and Tanae Rao, excluding the development of Squiggle by the Quantified Uncertainty Research Institute.
Epistemic Status: Somewhat confident. Despite out best efforts, it's likely there are some inconsistencies remaining in our work. We have aimed to make our claims and reasoning as easy to follow as possible. Uncertainty is quantified, but we are uncertain about many of our uncertainties! We are aware of several errors and areas of improvement, and try to highlight these explicitly. If you disagree with any of these claims, feel free to comment either on the EA Forum or in Observable. We intend to keep this notebook updated with any adjustments that need to be made.
Summary: We have quantified the uncertainty in GiveWell CEAs by translating them into Squiggle. This allows us to put a number on how uncertain we are about each of the cost-effectiveness parameters, and therefore the overall cost-effectiveness value of an intervention.
Quantifying uncertainty allows us to calculate the value of future research into the cost-effectiveness of interventions, and quantitatively see how funding this research might compare to donating to the current expected top charities.
As an example of this, we use our uncertainty quantification to calculate the Expected Value of Perfect Information on all GiveWell Top Charities, and find that the cost would outweigh the benefits if GiveWell were to spend more than 11.25% of their budget on research for this information. We then break down this value of information into the value of research into individual charities.
We also demonstrate how to estimate the value of information for individual parameters within a model, using the Catherine Hamlin Fistula Foundation as a case study. We believe this kind of analysis could help give a clearer idea of what, specifically, it would likely be cost-effective to research.

Introduction
GiveWell writes cost-effectiveness analyses to calculate and present how much good we can expect to do by donating to different charities. One of the most criticised components of their process for this is that they do not quantify uncertainty, meaning we don't know how sure they are about the estimated effectiveness of the charities. Quantifying uncertainty offers several benefits. Here, we will focus on one of the most significant of these - value-of-information analysis. We will also touch on how quantifying uncertainty can also improve calibration over time, communication and correctness.
We go through an example methodology for value-of-information analysis. We are uncertain about this exact methodology but believe value of information could be a helpful measure in the research pipeline, whether formally or informally calculated.
Uncertainty in the Cost-Effectiveness of GiveWell Charities
Our methodology for quantifying uncertainty in each of GiveWell's Top Charity CEAs are in the Supplemental Notebooks section below, alongside sensitivity analysis, per-country breakdowns, and additional considerations. In quantifying the uncertainty in these, we have attempted to be as faithful as possible to GiveWell's current CEAs. The purpose of this decision was primarily to investigate the impact of uncertainty quantification alone. We discuss other alterations that could be made in the Possible improvements to GiveWell models section.
After quantifying uncertainty in GiveWell top charities, we have found that the cost-effectivenesses of GiveDirectly, Against Malaria Foundation, Malaria Consortium, New Incentives, and Helen Keller International (all from GiveWell's top charity list) in 'doubling of consumption year equivalents per dollar' (DCYE/$) are distributed as follows.
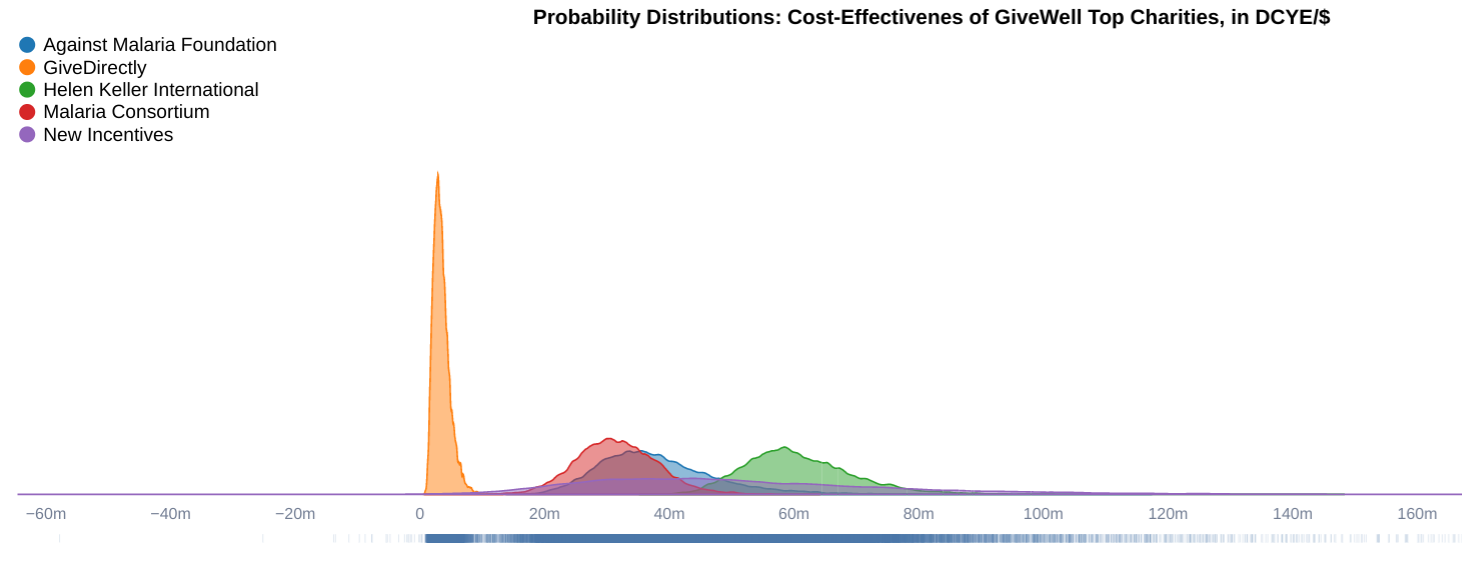
| Intervention | GiveWell | Our Mean | 95% CI | Diference |
| Against Malaria Foundation | 0.0375 | 0.0384 | 0.0234 - 0.0616 | +2.4% |
| GiveDirectly | 0.00335 | 0.00359 | 0.00167 - 0.00682 | +7% |
| Helen Keller International | 0.0541 | 0.0611 | 0.0465 - 0.0819 | +12.8% |
| Malaria Consortium | 0.031 | 0.0318 | 0.0196 - 0.0452 | +2.52% |
| New Incentives | 0.0458 | 0.0521 | 0.0139 - 0.117 | 13.8% |
What can we do with this information? It communicates the conventional decisions - GiveWell's top charities are at least 10x as effective as GiveDirectly, with Helen Keller International claiming the highest expected value. If we aim to donate to the charity with the highest expected value, all else being equal, why go to all the fuss of quantifying uncertainty?
Information about uncertainty is important because GiveWell doesn't only make decisions about what to donate to, but more frequently about what to research. Quantifying uncertainty in research provides inbuilt information about whether and where further research in that area is needed. Knowing how uncertain we are about existing research allows us to calculate what research directions are (and perhaps more importantly, are not) worth pursuing in the future. This is called the 'Value of Information' and can be calculated by Value of Information Analysis.
Value of Information
We can calculate the cost-effectiveness of charities by how many ‘units of value' they create per dollar, but we're uncertain about exactly how cost-effective each charity is. One way to navigate this is to present effectiveness values as probability distributions, showing how likely each possible value is the be the actual cost-effectiveness value for a given charity.
If we want to donate to the charity that can do the most good with our money, we could
a) donate to the charity we expect to be the most cost-effective based on our current best guesses (which, in this case, would be Helen Keller International); or
b) do more research so we can (hypothetically) know the actual effectiveness of the charities. For simplicity, let's imagine we could eliminate all uncertainty about all charities with this research.
We call the value we expect to get from knowing the effectiveness of a charity for sure, “Expected Value of Perfect Information,” or just "Value of Information." It’s equal to the difference between the amount of good we expect we could do with that knowledge and what we expect we could do without it. The concept of the Value of Information is intuitive and many questions relating to it can be answered without calculations. In the context of decision-making, information is more valuable when:
- It is more likely to change our mind about something, in a way that allows us to create more value with the decision
- The decision being made has higher consequences - a greater potential for producing value or harm, given the resources devoted to it
"Cost Ratio" is the maximum portion of a decision-maker's budget they could spend on obtaining this perfect information without the cost outweighing the expected benefit. Of course, this hypothetical research project does not perfectly reflect reality. No research project ever completely eliminates uncertainty. For this reason, the cost ratio could be considered a good upper bound for the amount worth spending on research into a given area. Douglas W. Hubbard of Hubbard Decision Research recommends spending but a tenth of this amount.
We call case (a) - where we donate to the expected best charity without researching - the "uniformed state." In this state, we only know the effectiveness of each charity as a probability distribution. The maximum cost-effectiveness we could expect to obtain in the uninformed state (U), in units of value per dollar, is simply the highest expected value of all the interventions considered:
If are random variables representing the cost-effectiveness for each of different interventions (such as those presented in the probability distributions above), and represents the intervention with the highest expected value - the one we expect to be the best before researching,
Where finds the expected value (mean) of , and finds the highest of these, considering every possible choice for .
(Links for more on max and E[X] notation)
We call case (b) - where we research all of the charities to find their true effectiveness - the "informed state." In this state, we know all the actual cost-effectiveness value for each of the charities, and the maximum value per dollar we could expect to generate would be the effectiveness of the charity with the highest actual cost-effectiveness value.
This expectation of value obtainable in the informed state can be calculated, but in practice, it is generally easier and just as useful to approximate it. To do this, we simulate a possible informed state by taking a sample of each random variable. This process can be iterated many times to produce a distribution of possible informed states and the values they yield. In each iteration, we would donate to the charity with the highest cost-effectiveness, and reap the value of that charity.. This process can be iterated many times to produce a distribution of possible informed states and the values they yield. In each iteration, we would donate to the charity with the highest cost-effectiveness, and reap the value of that charity.
The maximum cost-effectiveness we could expect to generate in the informed state (I) is the expected value of this distribution of values obtained assuming we chose the most effective charity for each iteration ().
Expected Value of Perfect Information (EVPI) about the true cost-effectiveness of an intervention, , in units of value per dollar, is how much effectiveness we could expect to gain in the informed state compared to the uninformed:
The amount of value we can expect to generate in the uninformed state, with the amount of money we have available is given by
where is the amount donated.
The amount of value we can expect to generate in the informed state, with the amount of money we have to available , and the cost of research , is given by:
Where is the cost of research and is the amount donated.
If research is worthwhile (cost does not outweigh benefits), we can expect to generate no less value in the informed state, than in the uninformed state:
From this, we can find a maximum cost ratio, cost of research : total amount available, for which net value is likely to be added by research. For instance, if we have $100,000 to donate, and a cost ratio of 20%, then the maximum amount it would be worth spending on research to eliminate all uncertainty would be $20,000. This should be considered an upper bound for research expenditure because in reality, we can only ever reduce uncertainty, which is necessarily less valuable. Consequently, we recommend a more conservative approach of spending closer to a tenth of the cost ratio on research (value of imperfect information). In this case, that means spending no more than $2,000 on research.
We use calculus to show what these values mean and how we could calculate them in terms of probability density functions, and look at the special case of investigating only one charity at a time in the appendix.
We can also sample real distributions to calculate this in Squiggle!
voi(c) = mean(SampleSet.mapN(c, {|xs| max(xs)}))
vou(c) = max(map(c, {|x| mean(x)}))
vpi(x) = voi(x) - vou(x)
charities = [givedirectly, helen_keller_international, new_incentives, malaria_consortium, amf_effectiveness]
vpi(charities) // Returns 7.74·10-3This is the expected units of value per dollar gained by eliminating all uncertainty in all charities. However, whether we should research to reduce uncertainty is dependent on two factors:
- Research costs - information that would cost more of our finite resources to acquire should be justified by a higher value of information.
- Size of investment - the greater the amount of money or other resources a decision is directing, the more important it is for that decision to be informed.
Now, we can calculate the cost ratio, or proportion of GiveWell's budget it would be worth devoting to research that would reduce uncertainty in their Top Charities, relative to the cost of this research:
vpi_cost(x) = {
my_voi = voi(x)
cost_ratio = (my_voi - vou(x)) / my_voi
cost_ratio
}
vpi_cost(charities) // Returns 0.113This means that GiveWell should spend no more than 11.3% of their budget on researching this their current Top Charities. This number is assuming that research would acquire perfect information. As this would not be the case and research would only decrease uncertainty, 10% of this value, or 1.13% of GiveWell's budget, may be a more appropriate amount.
We can also calculate the value of information on each GiveWell Top Charity individually. We do this by assuming the charities that we don't want to research have already reduced all their uncertainty and are set to their expected value, such that there is no value of researching any charity other than that/those selected[1].
| Charity under Research | VPI Cost ratio |
| Against Malaria Foundation | 0.4% |
| GiveDirectly | 0% |
| Helen Keller International | 0.75% |
| Malaria Consortium | 0% |
| New Incentives | 10.3% |
This indicates that it's valuable to reduce the uncertainty of current GiveWell top charities (at least, assuming the uncertainties specified in the supplemental notebooks). However, GiveWell is also focused on new interventions. Below is an example of how we evaluate the value of information for a new intervention.
Evaluating New Interventions, a Case Study with the Catherine Hamlin Fistula Foundation
GiveWell has previously investigated the Fistula Foundation, evaluating the effectiveness of surgically treating obstetric fistulas in low-income countries, seemingly considering both the quality of life detriments and loss of income engendered by fistulas. However, the Catherine Hamlin Fistula foundation, which may be easily overlooked because of its similarity to the Fistula Foundation in name and approach to treatment, is a different charity which focuses on treatment but also prevention and rehabilitation.
Quantifying uncertainty allows us to evaluate this charity, using rough numbers and informed guesses to give us an idea of cost-effectiveness. This can then inform a quick value of information analysis indicating how valuable further research into this intervention is likely to be.
Hannah Rokebrand has used this method to do a rough three-day analysis of CHFF's cost-effectiveness.
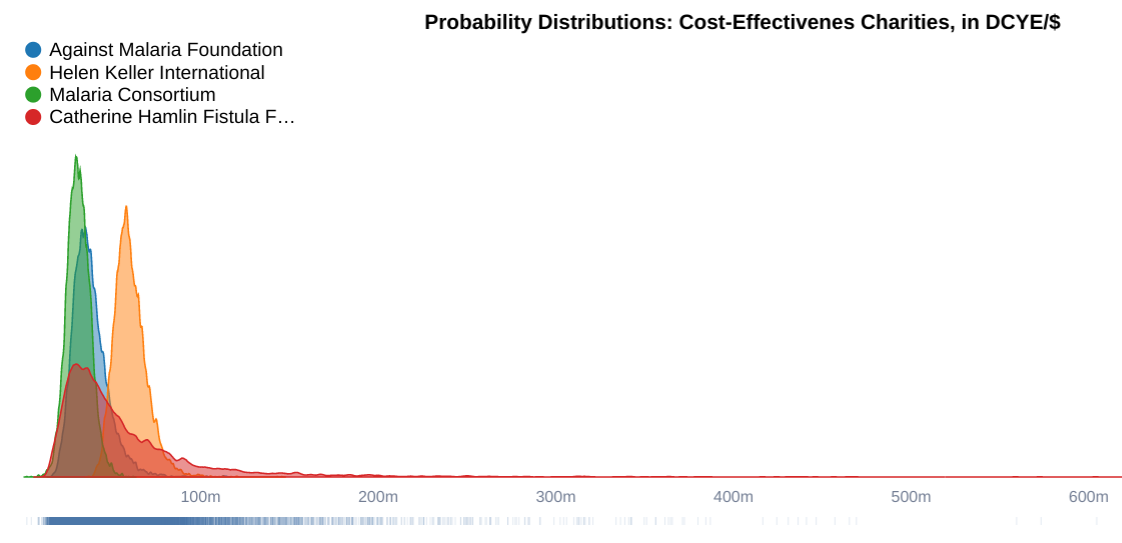
CHFF expected value: 0.057 doubling of consumption years equivalent
The above probability distributions show the probable cost-effectiveness values of three GiveWell top charities and the Catherine Hamlin Fistula Foundation in 'doubling of consumption year equivalents per dollar'. We can use these distributions to calculate the value of reducing all uncertainty about CHFF.
cost_ratio_fistula = vpi_cost([SampleSet.fromDist(mx(vou(charities))), fistula_foundation]) // returns 0.17This means, assuming our quantification of uncertainty, GiveWell should spend no more than 17% of their budget acquiring information about CHFF overall.
However, research projects often focus on specific variables within a CEA. We can find the most useful parameters to focus on in this case by calculating Expected Value of Perfect Partial Information.
Expected Value of Perfect Partial Information
Once we've found that CHFF is worth researching, we can calculate the value of using our finite resources to reduce uncertainty in only a selection of the parameters that contribute to its cost-effectiveness, to maximise the benefit of researching this intervention.
We take the cost-effectiveness of CHFF to be a function , which operates on a n parameters to produce a final cost-effectiveness probability distribution.
Again, the value per dollar we can expect to generate in the "uninformed state" is the expected cost-effectiveness of the charity with the highest expected value, in this case, we will take that to be HKI. We will again refer to this charity as .
In the informed state, we would know the exact value of one of the parameters, say . We would then donate to the charity with the highest expected value given this information - either HKI or CHFF.
We then want to find the expected value of the informed state over all possible values of .
If is the expected value excluding the variable , and returns a distribution of expected values over different possible values of Y_iYi)
We can then estimate the Expected Value of Partial Perfect Information (EVPPI) about CHFF from eliminating uncertainty about one parameter by calculating the difference between these values .
We can run these calculations in Squiggle, but this is a somewhat expensive operation and requires running the entire model ff thousands of times (for every sample). To simplify, we've approximated the value of information on each parameter by assuming , although this is not necessarily the case.
mapDict(x, f) = Dict.fromList(map(Dict.keys(x), {|key| [key, f(x[key])]}))
mapSet(x, key, value) = Dict.merge(x, Dict.fromList([[key, value]]))
to_mean(x) = mapDict(x, mean)
vpi_analysis(f, params, other) = {
mean_params = to_mean(params)
Dict.fromList(map(Dict.keys(params), {|key| [key, {
possible_results = f(mapSet(mean_params, key, params[key]))
vou = max([mean(possible_results), other])
possible_decisions = SampleSet.map(possible_results, {|s| max([s, other])})
voi = mean(possible_decisions)
vpi = voi - vou
vpi / voi
}]}))
}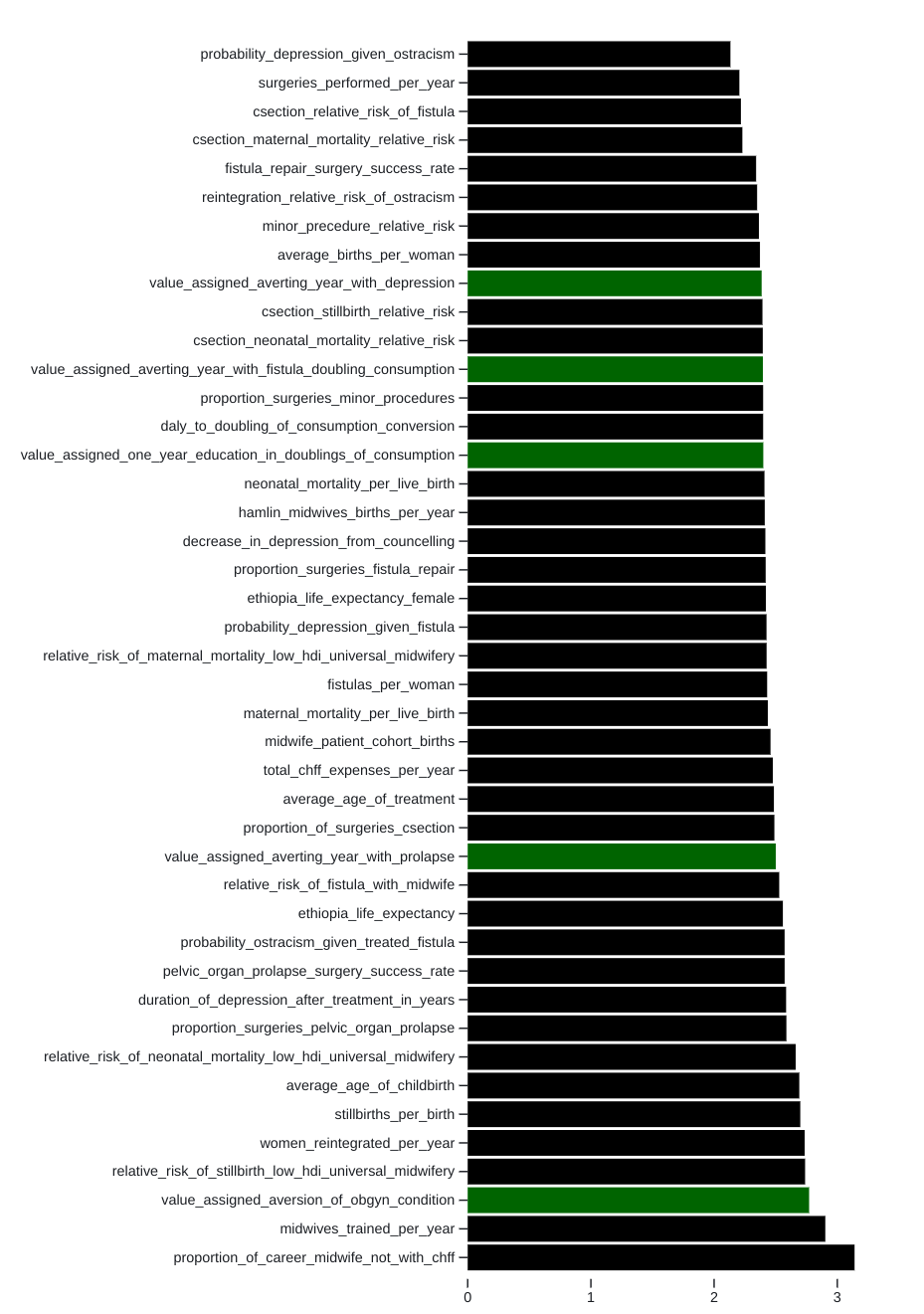
The calculations run in Squiggle find the cost ratio of researching each parameter contributing to our calculations of CHFF's cost-effectiveness. These indicate that the average number of midwives trained per year (midwives_trained_per_year) and portion_of_career_midwife_not_with_chff are the most impactful parameter for us to research to bring us closer to the true cost-effectiveness of CHFF.
Other Benefits of Uncertainty Quantification
Although we are fans of the value of information, there are several other benefits to uncertainty quantification, some of which we'll mention here.
Communication
Every measurement or observation we make is subject to uncertainty, and cannot know our calculated values to a greater level of certainty than the observed values from which they were calculated. Researchers commonly use error bars to help communicate the degree of this uncertainty so that we can compare and weigh different sources of evidence and consider the probability of results arising from the factors to which they are attributed, rather than random chance.
Quantifying uncertainty in the form of distributions also retains a dimensionality obscured by error bars. Distributions have a shape and can be combined in calculations to give us the shapes of distributions for calculated parameters, far more easily and precisely than current conventional methods of accounting for uncertainty.
In a post explaining a name change of GiveWell's fund for the most rigorously evaluated charities meeting its cost-effectiveness bar, a new criteria of inclusion in the fund is highlighted: "that we have a high degree of confidence in our expectations about the impact of their programs."
It may also be noteworthy that GiveWell has "introduced a new giving option, the All Grants Fund. The All Grants Fund supports the full range of GiveWell’s grantmaking and can be allocated to any grant that meets our cost-effectiveness bar — including opportunities outside of our top charities and riskier grants with high expected value."
We believe quantifying uncertainty may ease decisions about inclusion and exclusion from the Top Charities list, as well as communication about these decisions. This communication could potentially highlight uncertain but high expected value opportunities for individuals or organisations with lower risk aversion to consider.
Calibration
In some types of research, we need to estimate parameters that are difficult or impossible to measure, such as how we should weigh different sources of evidence, or the value we assign to lives saved compared to economic gains. Charity cost-effectiveness analyses are a prime example of this. Many of GiveWell's parameters are "best guesses" based on the information available to them at the time. If these values were forecast as "we are 95% confident that this value lies between x and y," rather than "we expect this value to be z, but this is a rough estimate," these forecasts could be updated by further research and the scale of these updates could be used to calibrate future estimates and form a record of reliability for GiveWell's estimates, as we do with other types of forecasters.
Correctness
GiveWell aims to maximise the expected value of the charity to which they most heavily donate (with reasonable confidence), but they calculate the final expected values of charities by doing calculations with the expected values of the parameters contributing to it. This assumes that, if is a function that gives the cost-effectiveness of an intervention from n random variable parameters,
Although it's a very practical assumption (so practical, we use it as an approximate in our Expected Value of Partial Perfect Information), it is only true when is a linear map, which is usually not the case. All the CEAs discussed here have expected values of all the parameters set to GiveWell values, however, because of the nature of the distributions, the final expected value changes slightly.
Discussions
In this section, we'll go through a list of discussion points that came up in working with GiveWell models, but are not directly relevant to uncertainty quantification.
Possible Improvements to our Models
Model Uncertainty and Optimizer's Curse
None of our models, particularly CHFF, consider the possibility of the model itself being incorrect, and do not adjust to a prior. This may be worthwhile to avoid optimizer's curse.
More Information on GiveWell Funding Decisions
One improvement we hope to make in our Value of Information Analysis is a better model of how GiveWell makes allocation decisions. We have been unable to find publicly-available, detailed information about how GiveWell decides where to allocate its funds, although an overview of their system is available. We expect GiveWell may provide grants for the intervention they expect to have the greatest impact in each country they target, in which case the country-level estimates presented in our supplemental notebooks may be more applicable than the global aggregates used here. Pairing country-level data with the funding gap for each charity in each region would likely yield a higher value of information estimates than those in this notebook.
More Considerate Choices of Distributions
Currently, our uncertainty quantifications have been shaped by an aesthetic bias. This means that if a cost-effectiveness calculation presented itself with a significant probability in the negative, or extremely long tails, we assumed we were in error and 'fixed' the source of this unaesthetic presentation. It may be however, that the distributions are not nearly so aesthetic. When quantifying uncertainty, we found that the maths around 'other actors' and counterfactual donations could create somewhat poorly-behaved distributions.
Our analyses also currently use beta distributions for proportions and lognormal distributions for most other parameters. These choices was may not have been the most appropriate. We'd in interested in considering other distributions in the future.
Moral Uncertainty
GiveWell CEAs typically quantify the good done by an intervention in terms of the intervention's primary objective, e.g. lives saved. However, to make the cost-effectiveness of different interventions comparable, these are then converted into a general "unit of value."
GiveDirectly is a charity with a highly researched and economic-based (objective) impact, which gives it a comparatively low-uncertainty cost-effectiveness value. Because of this, GiveWell generally measures the effectiveness of other programs they evaluate against GiveDirectly, and incorporate its units ('doubling of consumption years') in the universal units of value, into which all other programs' cost-effectivenesses are converted - 'doubling of consumption year equivalents per dollar' (DCYE per dollar).
This conversion process requires answering tough questions like "how much do we value saving the life of a four year-old child compared to that of his 32 year-old mother, compared doubling the spending power of a family in poverty?"
For example, the value GiveWell assigns averting one death of a child under 5 from malaria is 116.9 DCYEs. This implies GiveWell's CEA's value averting this death equivalently to doubling consumption for 116.9 person-years. As explained in this talk, these figures are determined by a combination of GiveWell staff opinion, a GiveWell donor survey, and an IDInsight survey of beneficiary preferences (low-income individuals in Ghana and Kenya).
These moral weights are often the most contentious part of a GiveWell CEA, and can hold considerable uncertainty. One way of doing this would be worldview diversification, where we look into a range of possible values for moral parameters and optimise for the highest expected choice-worthiness.
Future lines of research related to moral uncertainty where quantified uncertainty could be useful include:
Incorporating uncertainty about beneficiary preferences. When participants in the IDInsight survey were asked about the value of life, their answers differed significantly depending on how the question was phrased. From an 'individual perspective,' averting an under-5 death was considered worth the equivalent of $40,763, while the 'community perspective' phrasing elicited a value of $91,049.
High uncertainty, exacerbated by methodological concerns, may deter GiveWell from weighting survey data more heavily. We are not arguing that survey data should be weighted more heavily, but incorporating quantified uncertainty into the CEA may make analysts more comfortable with weighing the data more heavily where warranted.
- Determining the value of information on the moral weights parameters. Obtaining this moral information if it is shown to be an effective use of GiveWell researchers' time, might include commissioning further beneficiary preference surveys, seeking preferences from a larger sample of stakeholders, spending more time on high-level considerations (e.g., using WELLBYs).
Correlated Uncertainties
To get estimates comparable to each other, GiveWell CEAs use many variables that are the same across different charities. These include moral variables such as the discount rate and the moral weights, as well as a number or adjustment factors.
Because each of our CEAs was built in its separate notebook. Variables that should have more correlated uncertainty do not correlate. This means that our value of information analysis, considers the situation where one charity has a higher moral weight for the value of a child under 5 than a different charity, which would be impossible and unfair. These inconsistencies also have implications unrelated to VoI.
To account for this, you may want to adjust our value of information estimates downwards. However, we're not sure about the extent of this adjustment.
Squiggle is capable of developing models with correlated uncertainty, however, we ran into performance issues with developing individual notebooks, and having all the notebooks relate to each other would likely only increase the problem.
Possible improvements to GiveWell models
Integration over age brackets
Nuno Sempere is to be credited with this idea, and may be able to explain it better. As a language, Squiggle makes integration a lot easier. Nuno has an example here.
Some of GiveWell's CEAs focus on age-dependent interventions, such as infant vaccination, and breakdown the impact of these by age group. We have considered converting this format into one where impact is continuously modelled across all ages. However, in our experience, this has proved difficult to apply to GiveWell CEAs for two main reasons.
- GiveWell CEAs, particularly for age-dependent interventions, frequently cite IMHE data which presents statistics like disease prevalence and mortality for discrete (typically 4-year) age brackets, rather than as a continuous trends. Even if this date were presented more continuously, it's it would be in a form that could be easily incorporated into a formulaic model of impact by age.
- GiveWell CEAs use the units of doubling of consumption year equivalents, which to our knowledge, are not used by any other major organisation and do not have a continuous formula behind them. Because the 'equivalent' component of a doubling of consumption year equivalent is calculated by a combination of the continuous DALY formula, and discrete data about large age brackets and the values of surveyed stakeholders, it is difficult to model these units continuously.
This is not to say that the process would be impossible, but more work is needed for us to understand how to consistently do it in a way that would add information that isn't present in the discrete presentation.
Dimensional Analysis
Using Dimensional Analysis, it's possible to identify implicit assumptions within a model that could be incorrect or missing. Sam Nolan has done this with GiveDirectly, identifying two implicit assumptions, and highlighting the potential for a continuous Present Value formula.
A Continuous Present Value formula models present value where there are no discrete payouts, but continuous payouts over time. This may model the situation better, as the present value is supposed to represent benefits that accrue over time and do not occur annually. However, the change has minimal impact on overall estimates of cost-effectiveness.
Supplemental Notebooks
Each intervention has its observable notebook that goes through the CEA calculations. As most top charities operate in multiple countries, the distributions shown in this notebook are global means. If we knew exactly what portion of a charity's budget would go to each country, we could refine our cost-effectiveness estimates or do a different analysis where we consider the most effective intervention-country pairing.
The supplemental notebooks, which account for most of our work on this project, and on which this notebook is built, are indexed below. They are in no way complete, and we are still trying to make them as accurate as they can be.
Uncertainty Quantification of GiveDirectly
Author: Sam Nolan
Sam Nolan has written a post on the EA forum about this model. This model brings up some interesting questions with implicit parameters, and the use of logarithmic vs isoelastic utility which increases GiveDirectly's utility by 11%. This is one of complete models.
It would be interesting to include Happier Lives Institute's evaluations of cash transfers in future.
Uncertainty Quantification of New Incentives
Author: Hannah Rokebrand
New incentives are likely the most in development-notebook. It currently has very large tails, and we are unsure whether this is due to New Incentives having a large theory of change or an oversight on our part.
Uncertainty Quantification of the Against Malaria Foundation
Author: Tanae Rao
This has an associated EA Forum post.
Uncertainty Quantification of Helen Keller International
Author: Sam Nolan
This model is close to complete. It may have minor errors. The written work is still in progress.
Uncertainty Quantification of the Malaria Consortium
Author: Hannah Rokebrand
Uncertainty quantification for Malaria Consortium is complete, but the written component is still in progress.
CEA of the Catherine Hamlin Fistula Foundation
Author: Hannah Rokebrand
The flow on effects of CHFF's program are difficult to calculate and with a high degree of certainty. However, early results calculated under high uncertainty seem to show this intervention to worth further research.
This is a very rough calculation, missing a number of variables which may affect the value generated. Several uncertainty bounds are also rough estimates, or the results of very brief research. This post still needs a lot of refinement.
It would also be interesting to look at the cost-effectiveness of the three main areas of CHFF, prevention, treatment and rehabilitation and reintegration. Unfortunately, data about the total cost of these individual areas does not seem to be available, only CHFF's total expenses.
Value of Information on GiveDirectly
Author: Sam Nolan
This has an associated EA Forum post. This is a simple example of the value of information that I made to demonstrate the concept. This notebook doesn't serve a role in any of the calculations or results.
Appendix: Value of Information with Calculus:
This is an example of a special case of VoI where we are comparing the cost-effectiveness of charities (no consideration of risk or profit, only value per dollar), investigating only one at a time (rather than eliminating all uncertainty in all options at once), although this method could be extended by comparing each of n charities to the new expected best charity for every iteration. Calculating the value of information for all charities in a set is important because it we always be greater than the value of information from investigating only one charity, and as such may be used as un upper bound for the possible value to be gained from researching the charities in the set. This is particularly useful for larger sets, and can be calculated almost instantly using Squiggle. However, in practice we are more likely to be making decisions about investigating one intervention at a time, and the concepts explored here may be more intuitive from this application.
Case (a) (Without Research)
The units of value per dollar we could expect to obtain in the uninformed state (U):
If is a set of random variables representing the cost-effectiveness for each of n different interventions (such as those presented in the probability distributions above), is the probability density function of the intervention represented by , and represents the intervention with the highest expected value - the one we expect to be the best before researching,
Case (b) (With Research)
The units of value per dollar we could expect to obtain in the informed state (I):
Expected Value of Perfect Information (EVPI) about the true cost-effectiveness of in units of value per dollar, is how much more effectiveness we could expect to get in the informed state than in the uninformed:
The Cost Ratio, i.e. upper bound of the proportion of the total money we have available that we should be willing to invest in research, can be found by assuming that research is only worthwhile if we expect to obtain no less value in the informed state than in the uninformed state:
- ^
In the observable version of this post, there is a widget you can use to calculate how much value there is in researching different collections of interventions.
Relevant Resources
- Smith, James & Winkler, Robert. (2006). The Optimizer’s Curse: Skepticism and Postdecision Surprise in Decision Analysis. Management Science. 52. 311-322. 10.1287/mnsc.1050.0451.
- A Practical Guide to Value of Information Analysis follows a similar methodology to what we have used here, but accounts for factors that weren't relevant in our calculations, and does not combine probability distributions, which leads to the maths appearing notably more complex than ours.
Wilson, E.C.F. A Practical Guide to Value of Information Analysis. PharmacoEconomics 33, 105–121 (2015). https://doi.org/10.1007/s40273-014-0219-x - Value of information analysis for assessing risks and benefits of nanotechnology innovation represents a typical approach to VoI in healthcare decision-making. The decision options (proceeding or not proceeding with in intervention) are binary while ours (which intervention to fund) are not. This analysis also considers potential risks as well as benefits, and different approaches to risk aversion. We have only looked at benefits since the potential risks of donating to a GiveWell top charity are considered negligible.
Zabeo, A., Keisler, J.M., Hristozov, D. et al. Value of information analysis for assessing risks and benefits of nanotechnology innovation. Environ Sci Eur 31, 11 (2019). https://doi.org/10.1186/s12302-019-0194-0 - Dr Stefano Canessa of the British Ecological Society offers an extended simple explanation of VoI, particularly as it relates to ecology in his 2015 Methods Blog, The Value of Information: Does More Data Mean Better Decisions?
- Vaniver gives an overview of some LessWrong applications of VoI in their Value of Information: Four Examples
B. Yet, A. Constantinou, N. Fenton and M. Neil, "Expected Value of Partial Perfect Information in Hybrid Models Using Dynamic Discretization," in IEEE Access, vol. 6, pp. 7802-7817, 2018, doi: 10.1109/ACCESS.2018.2799527.
Acknowledgements
This work was supported by two EA Infrastructure Grants. We are grateful to the Quantified Uncertainty Research Institute for their work on the Squiggle language that made this all possible. We would also like to thank David Reinstein, Nuno Sempere and Falk Lieder for their feedback on this work.

Thanks for your entry!
This is really nice, major kudos for a) the result, b) pulling the research colaboration off. Also keen to see people build upon these, e.g., with the optimizer's curse.
Correlated uncertainty driven by using the same parameters across models: I'd love to see this, I expect it will effect the VOI calculations.
Also could be a good gateway towards the more difficult correlated uncertainty: the correlation between parameters within a model. I expect some of these to be highly correlated, and this might matter a lot. In fact, in the fistula model, some of these might largely be different takes on the same uncertain underlying variable? Here one might need to report on the VOI for something like a 'cluster of variables'?
But this is more challenging; I guess it would probably start with some calibrated judgment/educated guessing on the correlation parameter.
I think maybe the issue of correlated uncertainty is the biggest limitation to bringing uncertainty into the models. If the uncertainties are 'super correlated in the same direction' then the naive 'worst case/best case' for everything is closer to being correct. If the uncertainties are 'super negatively correlated' then we may need to worry less about uncertainty, or perhaps worry about the largest of the uncertainties.
Small point: I would replace 'budget' with 'funds they expect to influence'; considering the time horizon for this is difficult though, it probably requires a model of how the benefit of the research evolves over time, and some sort of explore/exploit modeling;
Finger-exercise: If we think GW influences 500 million per year over the next 10 years, or 5 billion in total, 11% is 550 million, 1% 55 million. ... or 5.5 million per year. (But as I said in the other comment, I don't know where that '1/10th rule' came from).
I guess this assumes that all of the money they shift are allocated to the single top-EV charity.
https://www.givingwhatwecan.org/charities/givewell-unrestricted-fund suggests their operating expenses are about $11 million per year. But:
But of course this doesn't count the VOI for the arrival of new charities, which could justify a greater expense.
Is there any basis for Hubbard's 'spend 1/10th of the max' rule of thumb? It seems arbitrary. Is there any evidence or information-theoretic justification for this?
On a related note, one could make a case that the 'benefit of research for informing Givewell's decisions' might understate the global benefits, if the research informs other research and decisionmaking outside of GW.
The VOI simulation calculation discussion you give ("This expectation of value obtainable in the informed state) is super-interesting to me, not sure I've seen this laid out before, I love it!.
Maybe you could add 1 or 2 more lines or footnotes to make it a bit clearer; I had to think through 'yeah these distributions represent our beliefs over the probability of each actual value for each charity ... so sampling from these reflects what we can expect to learn.' Maybe it just took me a moment because I didn't start out as a Bayesian.
Also, I might state the VOI as
I would want to disambiguate this so as to not be confused with a case where the context is high-stakes, but we are trying to choose between 'purple bednets and pink bednets' (nearly equivalent value)
What do you think?
I see a potential 'buried headline' here. It seems as though Helen Keller more or less 'dominates' the other charities!
Stepping outside the model itself, how confident are you in this result?