I got this idea after I read a few of CE (Charity Entrepreneurship) cost-effectiveness estimates when I was preparing my application for the CE research training program. Although this is not a major pressing improvement, this definitely is an iterative improvement over the current methodology and I haven’t seen anyone else raising this point yet.
CE uses DALYs averted as a measure of impact:
- DALYs (Disability-Adjusted Life Years): A measure of disease burden, expressed in years lost to disability or early death. Dying one year before your expected life span causes 1 DALY. DALYs are averted when we save someone from dying early, or when we reduce the number of sick people or the duration of their sickness. DALYs for a disease are the sum of YLLs and YLDs: .
- Years of Life Lost (YLLs): Calculated as the difference between the age at death and the life expectancy. Death is the worst possible outcome, and it gets one DALY per person per year.
- Years Lived with Disability (YLDs): Calculated by multiplying the severity of an illness or disability by its duration.
- DALYs averted: I like to think of DALYs averted as the difference between DALYs without intervention and DALYs with intervention. This captures the notion of counterfactuality, meaning our estimate should reflect the difference between a world where the intervention happened and one where it didn't.
For example, if an intervention saves a person who would have otherwise died at 30 and the life expectancy is 70, 40 YLLs are averted (without considering temporal discounting and age-weighing). If the intervention reduces a year of severe disability (with a disability weight of 0.5), 0.5 YLDs are averted.
When Charity Entrepreneurship estimates the number of DALYs that an intervention would avert, it uses a pre-made table by GiveWell. This table includes age weighting (which gives years in around 20-30 more value) and applies temporal discounting at 4% per year. CE uses the average values (last column).
Table 1: GiveWell estimates of value of life saved at various ages of death. The table is available here and made using a formula that you can find here.
| Age of death | Life expectancy (years) | YLL incorporating discount and age-weighting | |||
| Females | Males | Females | Males | Average | |
| 0 | 82.5 | 80 | 33.13 | 33.01 | 33.07 |
| 5 | 77.95 | 75.38 | 36.59 | 36.46 | 36.53 |
| 15 | 68.02 | 65.41 | 36.99 | 36.80 | 36.90 |
| 30 | 53.27 | 50.51 | 29.92 | 29.62 | 29.77 |
| 45 | 38.72 | 35.77 | 20.66 | 20.17 | 20.41 |
| 60 | 24.83 | 21.81 | 12.22 | 11.48 | 11.85 |
| 70 | 16.2 | 13.58 | 7.48 | 6.69 | 7.09 |
| 80 | 8.9 | 7.45 | 3.76 | 3.27 | 3.52 |
| 90 | 4.25 | 3.54 | 1.53 | 1.30 | 1.42 |
| 100 | 2 | 1.46 | 0.57 | 0.42 | 0.50 |
CE takes the exact values from the table. When an intervention saves someone who is 30 years old they literally take the value 29.77 DALYs which only includes temporal discounting and age-weighing.
This implicitly assumes that the subject would live a perfectly healthy life to the life expectancy used in the estimation. The full value of e.g. 29.77 DALYs averted was calculated assuming the subject lives healthy to the life expectancy. He is not going to — The subject is almost definitely going to get sick and will fail to realize the full value.
Why This Matters
We want our cost-effectiveness analyses (CEAs) to measure counterfactual impact. The difference between the world where the intervention happened and the one where it didn't should be the key result. If we take the full value of the life saved, we will overestimate the value by the DALYs the subject will incur while being sick. This is crucial when choosing between interventions that improve lives compared to interventions that save lives.
Is CE really making this mistake?
I’m pretty sure they do. Here, I try to show the exact place where it happens.
Typically, a CEA by CE will feature “standard inputs” sheet with this table:
Table 2: Standard inputs table included in a typical CEA made by CE.
| Age of death | DALYs (weighted) |
| 0 | 33.07 |
| 5 | 36.53 |
| 15 | 36.9 |
| 30 | 29.77 |
| 45 | 20.41 |
| 60 | 11.85 |
| 70 | 7.09 |
As you can see, this is a shortened version of the table 1 above. This table is later used when estimate the total impact.
Childhood vaccination reminders and encouragement (report) (CEA)
I’m not going to include the exact formula for impact here — I think it would make my point less understandable. The core argument is based on the fact that those exact values from the table are used and are usually only later discounted by 4% yearly, which does not offset for the suffering the subjects will experience by living a typical life. Open the sheet (same link as link to CEA above) and take a look and follow my reasoning:
The final formula for the DALYs averted is:
=NPV($C$125,163:163) + NPV($C$125, 170:170)
It comes from the cell C175. This is the sum of:
- DALYs equivalent of cost incurred by the beneficiaries discounted by 4% every year
- DALYs coming from deaths averted, discounted by 4% every year
Those values come from this table:
Table 3:
| Benefits – impact numbers (deaths averted) | |
| Deaths averted <1 yr | 51.06 |
| Deaths averted 1-4 yr | 144.17 |
| Deaths averted 5-14 yr | 1.55 |
| Deaths averted 15-49 yr | 3.48 |
| Deaths averted 50-74 yr | 9.34 |
| Total | 209.60 |
| Benefits – impact numbers (DALY averted) | |
| DALYs averted <1 yr | 1,688.53 |
| Deaths averted 1-4 yr | 5,266.46 |
| Deaths averted 5-14 yr | 57.06 |
| Deaths averted 15-49 yr | 70.98 |
| Deaths averted 50-74 yr | 66.25 |
| Total | 7,149.28 |
| Costs (disbenefits) to beneficiaries | |
| Income doublings | -110.5 |
| DALY equivalents | -48.0 |
| DALY equivalents (assume 5% less uptake per year) | -48.0 |
It represents the impact of the organization in one year. The deaths averted are translated to DALYs using formula:
Number of deaths averted × Value of averting death at that point in DALYs
The value of averting death comes from the standard inputs table mentioned eariler.
Behavioral interventions to support snakebite prevention and control (report) (CEA)
Snakebites CEA explicitly assumes that the value of life saved is 30 DALYs for someone who would otherwise die at the age of 30.
Table 4: Key Assumptions in Behavioral interventions to support snakebite prevention and control
| Key assumptions | ||||
| Discount rate | % | 4.0% | ||
| Probability of success | % | 66% | ||
| DALYs averted per snakebite (Health + Economic) | DALY | 5 | See Health and financial burden tab. | |
| DALYs averted per death averted | DALY | 30 | Median age of death is 30 | https://www.thelancet.com/action/showPdf?pii=S2214-109X%2822%2900028-6 |
Can we fix this?
Yes, we can fix this fairly easily. We should decrease the number of DALYs gained from interventions (or components of interventions) that saves lives by roughly 10%.
To get that number I used data from Global Burden of Disease Study to get a rough number of YLDs that one will suffer when living in World Bank income regions:
Figure 1: age-standardized rates of YLDs per World Bank income regions since 1990 to 2020.
Here is a table of YLDs one would suffer on average living in those regions in 2021 (basically the rates above but divided by 100 000):
Table 5: Average number of YLDs one would suffer per year living in a given WHO income region.
| WHO income region | YLDs |
| Global | 0.11 |
| High-middle SDI | 0.09 |
| High SDI | 0.11 |
| Low-middle SDI | 0.11 |
| Middle SDI | 0.10 |
| Low SDI | 0.12 |
The formula for the number is the table above is:
For more accurate calculations of YLDs, we could categorize individuals by age groups and determine the average YLDs for specific age groups. However, the online data visualization tool provided by the Global Burden of Disease study only gives age-standardized YLDs for all ages.
The graph above shows that the variance in the rates isn’t high—they are limited between 12.4k and 9.6k since 1990. This consistency is a good sign that we can use these estimates for future projections. Besides that, the values closer in the future matter more for the adjustment since they aren’t discounted yet.
I think this is an improvement over current CE methodology, but I’m still unsure about some of my thoughts:
- I don’t know if the methodology changed since 1990 and how consistent those numbers are.
- I’m also not sure if the YLDs are comparable between countries. I expect that an YLD in a High SDI might be worth less than a YLD in Low SDI.
- This can be a major mistake for interventions that save a life but leave the person with some extra disability.
Update after getting feedback from CE:
After sending this post for a review to CE I did some further research based on their questions and things CE was not sure about:
Is this built into the formula for the value of saving a life somehow?
The formula for the value of saving a life at a specific age that is used to create the standard inputs table is quite complicated:
Figure 2:
Where does it come from? From this document. I will try to explain it: intuitively, Given age of death a and life expectancy L the value of saving a life is:
which translates to:
I tried to integrate the above formula (just to check if the both come out to the same) but I failed so I recreated it using numerical approximation in Python to confirm that there isn’t any kind of discount factor going into there besides age-weighing and temporal discounting, and I compared the results from my function to the results from the ‘standard inputs’ sheet. They are the same. The complex function above only include age-weighing and temporal discounting.
Can discount rate account for that?
The discount rate reduces the benefits later in time by an increasing factor. The adjustment I’m suggesting should probably remain constant or diminish over time to account for improving healthcare, which decreases the YLDs people suffer. Crucially, we start with the full value of 10% immediately. The discount rate decreases the gains further in the future, which contrasts with my suggested improvement.
Can age-weighing account for that?
The reduction of DALYs I’m writing about, should reduce the total value of saving a life while age-weighting shits it around. They function differently. Additionally, I checked how age weighting without discounting, given the B and C parameters used by GiveWell, changes the value of saving lives:
Figure 3: DALYs averted by saving a life of 20 year old and 0 year old give life expectancy = x
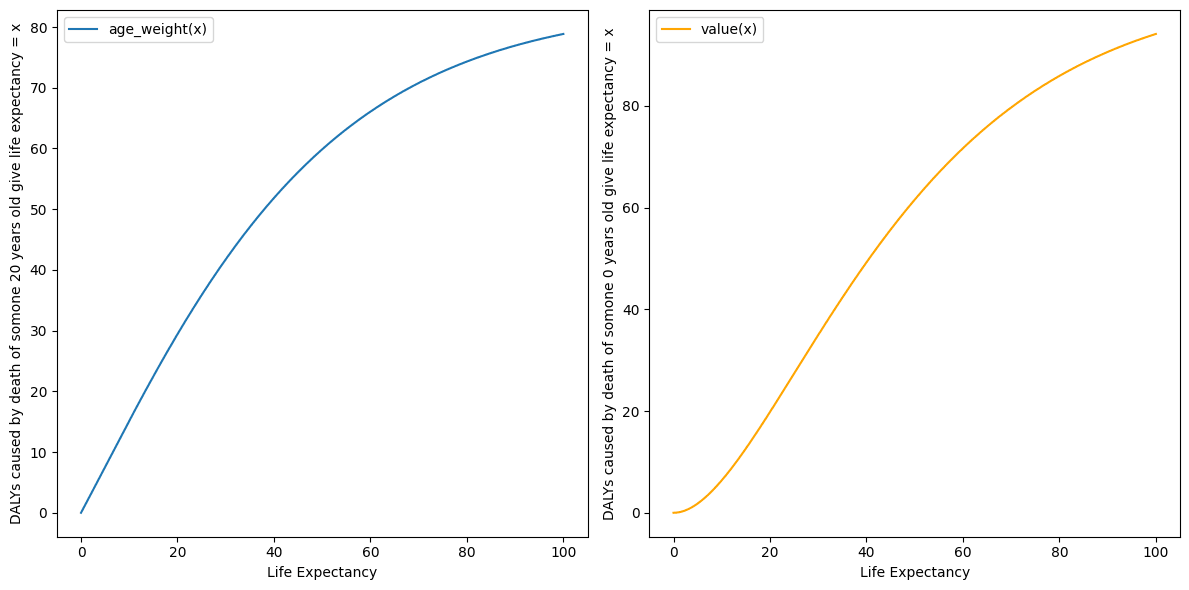
It turns out, if not discounting, you would actually get more DALYs by saving an 0 year old who would othwerwise live 60 years you can get almost 70 DALYs!
Other random ideas that might be even more important than the main point
Is GiveWell also making this mistake?
They don’t. I briefly read GiveWell 2024 CEA, GiveWell's CEA of insecticide-treated net, GiveWell's 2020 moral weights and GiveWell doesn’t try to estimate DALYs averted in their estimates but instead of that decided to use “units of value”:
Deaths averted at different ages
We combined the donor preferences with years of life lost (YLLs) and with past staff weights, using years of life lost as a proxy for the IDinsight survey (because they look broadly similar, but the IDinsight survey results are too jagged to use wholesale) and using James Snowden's 2018 moral weights as a proxy for GiveWell staff (because his weights were near the median and he had provided a complete set of age groups).
We weighted these sources as follows:
- 60% weight on donor responses
- 10% weight on James Snowden's 2018 weights (as a proxy for 2018 GiveWell staff)
- 30% weight on YLLs (both as a commonly-used metric itself and as a proxy for the IDinsight survey)
Donor responses received the majority of the weight primarily because in our view, that curve represents the most plausible set of weights. In particular, the other two do not distinguish between early neonatal deaths and deaths at age one, which is an age range we're especially interested in.
We use donor weights as our result for stillbirths because we don't have data from the other sources on stillbirths.
GiveWell assessment is more nuanced but also less grouned in "real" DALYs which makes it harder to say if it includes the adjustment I'm suggesting. It might be that the weights coming from donors already adjust for that.



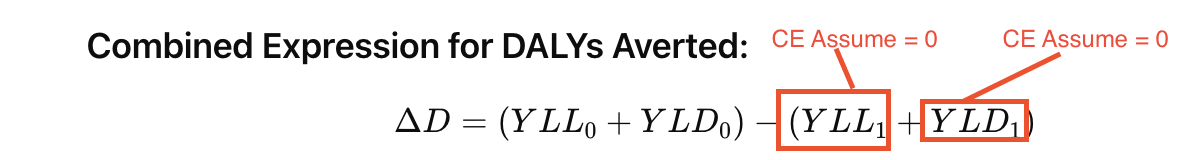



Disclosure: I discussed this with OP (Mikołaj) previous to it being posted.
Low confidence in what I am saying being correct, I am brand new to this area and trying to get my head around it.
I agree this is not a bad way to fix post-hoc. One concern I would have using this model going forward, is that you may overweight interventions that leave the beneficiary with some sort of long lasting disability.
Take the example of administering snakebite anti-venom, if we assumed that 1/2 of beneficiaries that counterfactually survive are likely to have lost a limb, if you don't account for that in your DALY's averted, then snakebite anti-venom's DALYs averted will be artificially inflated compared to an interventions who's counterfactual beneficiaries don't have high levels of Years Lived with Disability.