by Trevor Chow, Basil Halperin, and J. Zachary Mazlish
[November 2023 update: This post is now an academic paper, here, with some different emphasis and some new empirical evidence.]
In this post, we point out that short AI timelines would cause real interest rates to be high, and would do so under expectations of either unaligned or aligned AI. However, 30- to 50-year real interest rates are low. We argue that this suggests one of two possibilities:
- Long(er) timelines. Financial markets are often highly effective information aggregators (the “efficient market hypothesis”), and therefore real interest rates accurately reflect that transformative AI is unlikely to be developed in the next 30-50 years.
- Market inefficiency. Markets are radically underestimating how soon advanced AI technology will be developed, and real interest rates are therefore too low. There is thus an opportunity for philanthropists to borrow while real rates are low to cheaply do good today; and/or an opportunity for anyone to earn excess returns by betting that real rates will rise.
In the rest of this post we flesh out this argument.
- Both intuitively and under every mainstream economic model, the “explosive growth” caused by aligned AI would cause high real interest rates.
- Both intuitively and under every mainstream economic model, the existential risk caused by unaligned AI would cause high real interest rates.
- We show that in the historical data, indeed, real interest rates have been correlated with future growth.
- Plugging the Cotra probabilities for AI timelines into the baseline workhorse model of economic growth implies substantially higher real interest rates today.
- In particular, we argue that markets are decisively rejecting the shortest possible timelines of 0-10 years.
- We argue that the efficient market hypothesis (EMH) is a reasonable prior, and therefore one reasonable interpretation of low real rates is that since markets are simply not forecasting short timelines, neither should we be forecasting short timelines.
- Alternatively, if you believe that financial markets are wrong, then you have the opportunity to (1) borrow cheaply today and use that money to e.g. fund AI safety work; and/or (2) earn alpha by betting that real rates will rise.
An order-of-magnitude estimate is that, if markets are getting this wrong, then there is easily $1 trillion lying on the table in the US treasury bond market alone – setting aside the enormous implications for every other asset class.
Interpretation. We view our argument as the best existing outside view evidence on AI timelines – but also as only one model among a mixture of models that you should consider when thinking about AI timelines. The logic here is a simple implication of a few basic concepts in orthodox economic theory and some supporting empirical evidence, which is important because the unprecedented nature of transformative AI makes “reference class”-based outside views difficult to construct. This outside view approach contrasts with, and complements, an inside view approach, which attempts to build a detailed structural model of the world to forecast timelines (e.g. Cotra 2020; see also Nostalgebraist 2022).
Outline. If you want a short version of the argument, sections I and II (700 words) are the heart of the post. Additionally, the section titles are themselves summaries, and we use text formatting to highlight key ideas.
I. Long-term real rates would be high if the market was pricing advanced AI
Real interest rates reflect, among other things:
- Time discounting, which includes the probability of death
- Expectations of future economic growth
This claim is compactly summarized in the “Ramsey rule” (and the only math that we will introduce in this post), a version of the “Euler equation” that in one form or another lies at the heart of every theory and model of dynamic macroeconomics:
where:
- is the real interest rate over a given time horizon
- is time discounting over that horizon
- is a (positive) preference parameter reflecting how much someone cares about smoothing consumption over time
- is the growth rate
(Internalizing the meaning of these Greek letters is wholly not necessary.)
While more elaborate macroeconomic theories vary this equation in interesting and important ways, it is common to all of these theories that the real interest rate is higher when either (1) the time discount rate is high or (2) future growth is expected to be high.
We now provide some intuition for these claims.
Time discounting and mortality risk. Time discounting refers to how much people discount the future relative to the present, which captures both (i) intrinsic preference for the present relative to the future and (ii) the probability of death.
The intuition for why the probability of death raises the real rate is the following. Suppose we expect with high probability that humanity will go extinct next year. Then there is no reason to save today: no one will be around to use the savings. This pushes up the real interest rate, since there is less money available for lending.
Economic growth. To understand why higher economic growth raises the real interest rate, the intuition is similar. If we expect to be wildly rich next year, then there is also no reason to save today: we are going to be tremendously rich, so we might as well use our money today while we’re still comparatively poor.
(For the formal math of the Euler equation, Baker, Delong, and Krugman 2005 is a useful reference. The core intuition is that either mortality risk or the prospect of utopian abundance reduces the supply of savings, due to consumption smoothing logic, which pushes up real interest rates.)
Transformative AI and real rates. Transformative AI would either raise the risk of extinction (if unaligned), or raise economic growth rates (if aligned).
Therefore, based on the economic logic above, the prospect of transformative AI – unaligned or aligned – will result in high real interest rates. This is the key claim of this post.
As an example in the aligned case, Davidson (2021) usefully defines AI-induced “explosive growth” as an increase in growth rates to at least 30% annually. Under a baseline calibration where and , and importantly assuming growth rates are known with certainty, the Euler equation implies that moving from 2% growth to 30% growth would raise real rates from 3% to 31%!
For comparison, real rates in the data we discuss below have never gone above 5%.
(In using terms like “transformative AI” or “advanced AI”, we refer to the cluster of concepts discussed in Yudkowsky 2008, Bostrom 2014, Cotra 2020, Carlsmith 2021, Davidson 2021, Karnofsky 2022, and related literature: AI technology that precipitates a transition comparable to the agricultural or industrial revolutions.)
II. But: long-term real rates are low
The US 30-year real interest rate ended 2022 at 1.6%. Over the full year it averaged 0.7%, and as recently as March was below zero. Looking at a shorter time horizon, the US 10-year real interest rate is 1.6%, and similarly was below negative one percent as recently as March.
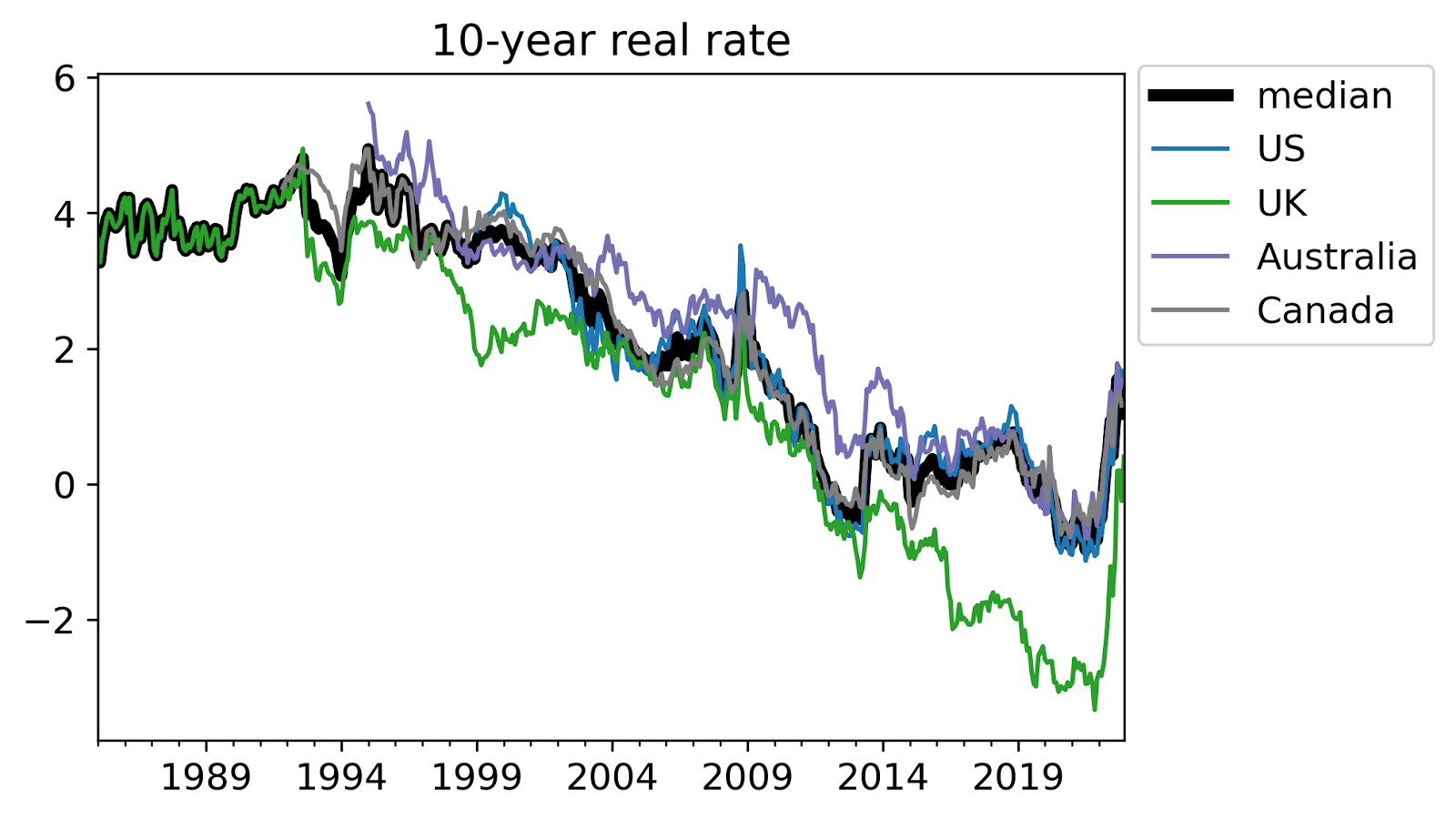
(Data sources used here are explained in section V.)
The UK in autumn 2021 sold a 50-year real bond with a -2.4% rate at the time. Real rates on analogous bonds in other developed countries in recent years have been similarly low/negative for the longest horizons available. Austria has a 100-year nominal bond – being nominal should make its rate higher due to expected inflation – with yields less than 3%.
Thus the conclusion previewed above: financial markets, as evidenced by real interest rates, are not expecting a high probability of either AI-induced growth acceleration or elevated existential risk, on at least a 30-50 year time horizon.
III. Uncertainty, takeoff speeds, inequality, and stocks
In this section we briefly consider some potentially important complications.
Uncertainty. The Euler equation and the intuition described above assumed certainty about AI timelines, but taking into account uncertainty does not change the core logic. With uncertainty about the future economic growth rate, then the real interest rate reflects the expected future economic growth rate, where importantly the expectation is taken over the risk-neutral measure: in brief, probabilities of different states are reweighted by their marginal utility. We return to this in our quantitative model below.
Takeoff speeds. Nothing in the logic above relating growth to real rates depends on slow vs. fast takeoff speed; the argument can be reread under either assumption and nothing changes. Likewise, when considering the case of aligned AI, rates should be elevated whether economic growth starts to rise more rapidly before advanced AI is developed or only does so afterwards. What matters is that GDP – or really, consumption – ends up high within the time horizon under consideration. As long as future consumption will be high within the time horizon, then there is less motive to save today (“consumption smoothing”), pushing up the real rate.
Inequality. The logic above assumed that the development of transformative AI affects everyone equally. This is a reasonable assumption in the case of unaligned AI, where it is thought that all of humanity will be evaporated. However, when considering aligned AI, it may be thought that only some will benefit, and therefore real interest rates will not move much: if only an elite Silicon Valley minority is expected to have utopian wealth next year, then everyone else may very well still choose to save today.
It is indeed the case that inequality in expected gains from transformative AI would dampen the impact on real rates, but this argument should not be overrated. First, asset prices can be crudely thought of as reflecting a wealth-weighted average across investors. Even if only an elite minority becomes fabulously wealthy, it is their desire for consumption smoothing which will end up dominating the determination of the real rate. Second, truly transformative AI leading to 30%+ economy-wide growth (“Moore’s law for everything”) would not be possible without having economy-wide benefits.
Stocks. One naive objection to the argument here would be the claim that real interest rates sound like an odd, arbitrary asset price to consider; certainly stock prices are the asset price that receive the most media attention.
In appendix 1, we explain that the level of the real interest rate affects every asset price: stocks for instance reflect the present discounted value of future dividends; and real interest rates determine the discount rate used to discount those future dividends. Thus, if real interest rates are ‘wrong’, every asset price is wrong. If real interest rates are wrong, a lot of money is on the table, a point to which we return in section X.
We also argue that stock prices in particular are not a useful indicator of market expectations of AI timelines. Above all, high stock prices of chipmakers or companies like Alphabet (parent of DeepMind) could only reflect expectations for aligned AI and could not be informative of the risk of unaligned AI. Additionally, as we explain further in the appendix, aligned AI could even lower equity prices, by pushing up discount rates.
IV. Historical data on interest rates supports the theory: preliminaries
In section I, we gave theoretical intuition for why higher expected growth or higher existential risk would result in higher interest rates: expectations for such high growth or mortality risk would lead people to want to save less and borrow more today. In this section and the next two, we showcase some simple empirical evidence that the predicted relationships hold in the available data.
Measuring real rates. To compare historical real interest rates to historical growth, we need to measure real interest rates.
Most bonds historically have been nominal, where the yield is not adjusted for changes in inflation. Therefore, the vast majority of research studying real interest rates starts with nominal interest rates, attempts to construct an estimate of expected inflation using some statistical model, and then subtracts this estimate of expected inflation from the nominal rate to get an estimated real interest rate. However, constructing measures of inflation expectations is extremely difficult, and as a result most papers in this literature are not very informative.
Additionally, most bonds historically have had some risk of default. Adjusting for this default premium is also extremely difficult, which in particular complicates analysis of long-run interest rate trends.
The difficulty in measuring real rates is one of the main causes, in our view, of Tyler Cowen’s Third Law: “all propositions about real interest rates are wrong”. Throughout this piece, we are badly violating this (Gödelian) Third Law. In appendix 2, we expand on our argument that the source of Tyler’s Third Law is measurement issues in the extant literature, together with some separate, frequent conceptual errors.
Our approach. We take a more direct approach.
Real rates. For our primary analysis, we instead use market real interest rates from inflation-linked bonds. Because we use interest rates directly from inflation-linked bonds – instead of constructing shoddy estimates of inflation expectations to use with nominal interest rates – this approach avoids the measurement issue just discussed (and, we argue, allows us to escape Cowen’s Third Law).
To our knowledge, prior literature has not used real rates from inflation-linked bonds only because these bonds are comparatively new. Using inflation-linked bonds confines our sample to the last ~20 years in the US, the last ~30 in the UK/Australia/Canada. Before that, inflation-linked bonds didn’t exist. Other countries have data for even fewer years and less liquid bond markets.
(The yields on inflation-linked bonds are not perfect measures of real rates, because of risk premia, liquidity issues, and some subtle issues with the way these securities are structured. You can build a model and attempt to strip out these issues; here, we will just use the raw rates. If you prefer to think of these empirics as “are inflation-linked bond yields predictive of future real growth” rather than “are real rates predictive of future real growth”, that interpretation is still sufficient for the logic of this post.)
Nominal rates. Because there are only 20 or 30 years of data on real interest rates from inflation-linked bonds, we supplement our data by also considering unadjusted nominal interest rates. Nominal interest rates reflect real interest rates plus inflation expectations, so it is not appropriate to compare nominal interest rates to real GDP growth.
Instead, analogously to comparing real interest rates to real GDP growth, we compare nominal interest rates to nominal GDP growth. The latter is not an ideal comparison under economic theory – and inflation variability could swamp real growth variability – but we argue that this approach is simple and transparent.
Looking at nominal rates allows us to have a very large sample of countries for many decades: we use OECD data on nominal rates available for up to 70 years across 39 countries.
V. Historical data on interest rates supports the theory: graphs
The goal of this section is to show that real interest rates have correlated with future real economic growth, and secondarily, that nominal interest rates have correlated with future nominal economic growth. We also briefly discuss the state of empirical evidence on the correlation between real rates and existential risk.
Real rates vs. real growth. A first cut at the data suggests that, indeed, higher real rates today predict higher real growth in the future:
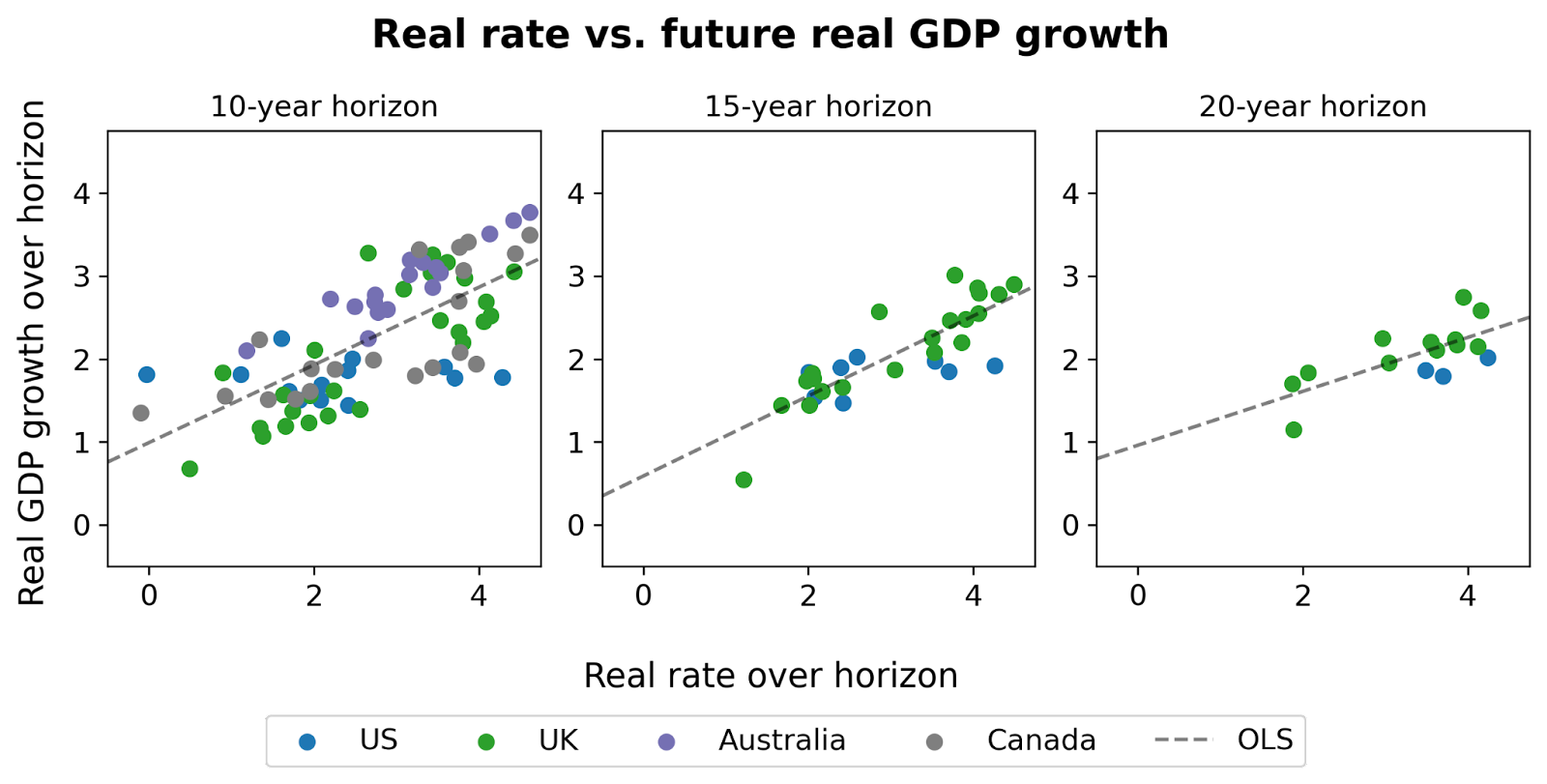
To see how to read these graphs, take the left-most graph (“10-year horizon”) for example. The x-axis shows the level of the real interest rate, as reflected on 10-year inflation linked bonds. The y-axis shows average real GDP growth over the following 10 years.
The middle and right hand graphs show the same, at the 15-year and 20-year horizons. The scatter plot shows all available data for the US (since 1999), the UK (since 1985), Australia (since 1995), and Canada (since 1991). (Data for Australia and Canada is only available at the 10-year horizon, and comes from Augur Labs.)
Eyeballing the figure, there appears to be a strong relationship between real interest rates today and future economic growth over the next 10-20 years.
To our knowledge, this simple stylized fact is novel.
Caveats. “Eyeballing it” is not a formal econometric method; but, this is a blog post not a journal article (TIABPNAJA). We do not perform any formal statistical tests here, but we do want to acknowledge some important statistical points and other caveats.
First, the data points in the scatter plot are not statistically independent: real rates and growth are both persistent variables; the data points contain overlapping periods; and growth rates in these four countries are correlated. These issues are evident even from eyeballing the time series. Second, of course this relationship is not causally identified: we do not have exogenous variation in real growth rates. (If you have ideas for identifying the causal effect of higher real growth expectations on real rates, we would love to discuss with you.)
Relatedly, many other things are changing in the world which are likely to affect real rates. Population growth is slowing, retirement is lengthening, the population is aging. But under AI-driven “explosive” growth – again say 30%+ annual growth, following the excellent analysis of Davidson (2021) – then, we might reasonably expect that this massive of an increase in the growth rate would drown out the impact of any other factors.
Nominal rates vs. nominal growth. Turning now to evidence from nominal interest rates, recall that the usefulness of this exercise is that while there only exists 20 or 30 years of data on real interest rates for two countries, there is much more data on nominal interest rates.
We simply take all available data on 10-year nominal rates from the set of 39 OECD countries since 1954. The following scatterplot compares the 10-year nominal interest versus nominal GDP growth over the succeeding ten years by country:
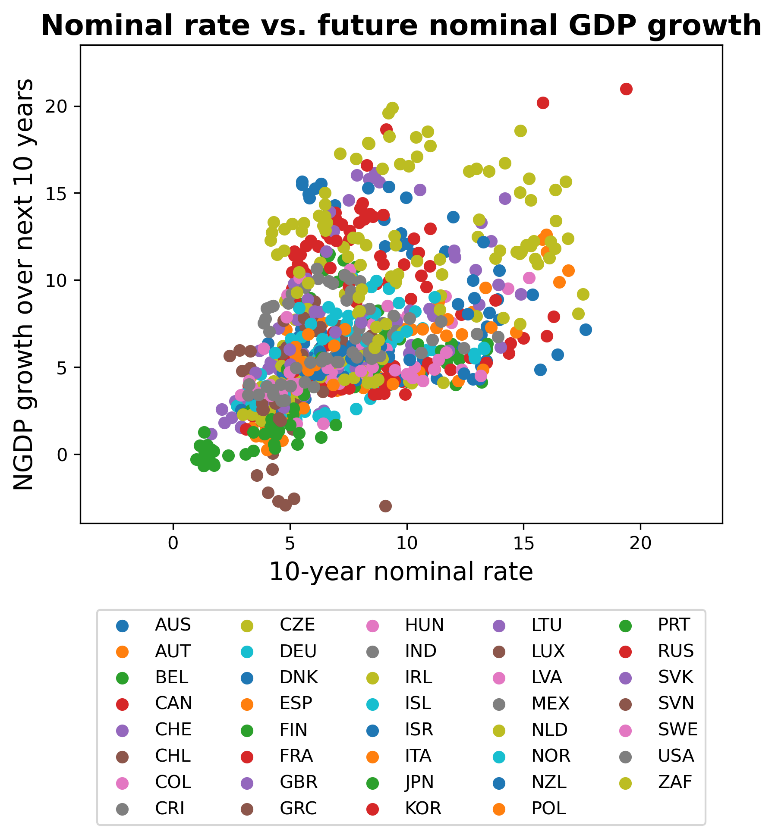
Again, there is a strong positive – if certainly not perfect – relationship. (For example, the outlier brown dots at the bottom of the graph are Greece, whose high interest rates despite negative NGDP growth reflect high default risk during an economic depression.)
The same set of nontrivial caveats apply to this analysis as above.
We consider this data from nominal rates to be significantly weaker evidence than the evidence from real rates, but corroboration nonetheless.
Backing out market-implied timelines. Taking the univariate pooled OLS results from the real rate data far too seriously, the fact that the 10-year real rate in the US ended 2022 at 1.6% would predict average annual real GDP growth of 2.6% over the next 10 years in the US; the analogous interest rate of -0.2% in the UK would predict 0.7% annual growth over the next 10 years in the UK. Such growth rates, clearly, are not compatible with the arrival of transformative aligned AI within this horizon.
VI. Empirical evidence on real rates and mortality risk
We have argued that in the theory, real rates should be higher in the face of high economic growth or high mortality risk; empirically, so far, we have only shown a relationship between real rates and growth, but not between real rates and mortality.
Showing that real rates accurately reflect changes in existential risk is very difficult, because there is no word-of-god measurement of how existential risk has evolved over time.
We would be very interested in pursuing new empirical research examining “asset pricing under existential risk”. In appendix 3, we perform a scorched-earth literature review and find essentially zero existing empirical evidence on real rates and existential risks.
Disaster risk. In particular, the extant literature does not study existential risks but instead “merely” disaster risks, under which real assets are devastated but humanity is not exterminated. Disaster risks do not necessarily raise real rates – indeed, such risks are thought to lower real rates due to precautionary savings. That notwithstanding, some highlights of the appendix review include a small set of papers finding that individuals with a higher perceived risk of nuclear conflict during the Cold War saved less, as well as a paper noting that equities which were headquartered in cities more likely to be targeted by Soviet missiles did worse during the Cuban missile crisis (see also). Our assessment is that these and the other available papers on disaster risks discussed in the appendix have severe limitations for the purposes here.
Individual mortality risk. We judge that the best evidence on this topic comes instead from examining the relationship between individual mortality risk and savings/investment behavior. The logic we provided was that if humanity will be extinct next year, then there is no reason to save, pushing up the real rate. Similar logic says that at the individual level, a higher risk of death for any reason should lead to lower savings and less investment in human capital. Examples of lower savings at the individual level need not raise interest rates at the economy-wide level, but do provide evidence for the mechanism whereby extinction risk should lead to lower saving and thus higher interest rates.
One example comes from Malawi, where the provision of a new AIDS therapy caused a significant increase in life expectancy. Using spatial and temporal variation in where and when these therapeutics were rolled out, it was found that increased life expectancy results in more savings and more human capital investment in the form of education spending. Another experiment in Malawi provided information to correct pessimistic priors about life expectancy, and found that higher life expectancy directly caused more investment in agriculture and livestock.
A third example comes from testing for Huntington’s disease, a disease which causes a meaningful drop in life expectancy to around 60 years. Using variation in when people are diagnosed with Huntington’s, it has been found that those who learn they carry the gene for Huntington’s earlier are 30 percentage points less likely to finish college, which is a significant fall in their human capital investment.
Studying the effect on savings and real rates from increased life expectancy at the population level is potentially intractable, but would be interesting to consider further. Again, in our assessment, the best empirical evidence available right now comes from the research on individual “existential” risks and suggests that real rates should increase with existential risk.
VII. Plugging the Cotra probabilities into a simple quantitative model of real interest rates predicts very high rates
Section VI used historical data to go from the current real rate to a very crude market-implied forecast of growth rates; in this section, we instead use a model to go from existing forecasts of AI timelines to timeline-implied real rates. We aim to show that under short AI timelines, real interest rates would be unrealistically elevated.
This is a useful exercise for three reasons. First, the historical data is only able to speak to growth forecasts, and therefore only able to provide a forecast under the possibly incorrect assumption of aligned AI. Second, the empirical forecast assumes a linear relationship between the real rate and growth, which may not be reasonable for a massive change caused by transformative AI. Third and quite important, the historical data cannot transparently tell us anything about uncertainty and the market’s beliefs about the full probability distribution of AI timelines.
We use the canonical (and nonlinear) version of the Euler equation – the model discussed in section I – but now allow for uncertainty on both how soon transformative AI will be developed and whether or not it will be aligned. The model takes as its key inputs (1) a probability of transformative AI each year, and (2) a probability that such technology is aligned.
The model is a simple application of the stochastic Euler equation under an isoelastic utility function. We use the following as a baseline, before considering alternative probabilities:
- We use smoothed Cotra (2022) probabilities for transformative AI over the next 30 years: a 2% yearly chance until 2030, a 3% yearly chance through 2036, and a 4% yearly chance through 2052.
- We use the FTX Future Fund’s median estimate of 15% for the probability that AI is unaligned conditional on the development of transformative AI.
- With the arrival of aligned AI, we use the Davidson (2020) assumption of 30% annual economic growth; with the arrival of unaligned AI, we assume human extinction. In the absence of the development of transformative AI, we assume a steady 1.8% growth rate.
- We calibrate the pure rate of subjective time preference to 0.01 and the consumption smoothing parameter (i.e. inverse of the elasticity of intertemporal substitution) as 1, following the economic literature.
Thus, to summarize: by default, GDP grows at 1.8% per year. Every year, there is some probability (based on Cotra) that transformative AI is developed. If it is developed, there is a 15% probability the world ends, and an 85% chance GDP growth jumps to 30% per year.
We have built a spreadsheet here that allows you to tinker with the numbers yourself, such as adjusting the growth rate under aligned AI, to see what your timelines and probability of alignment would imply for the real interest rate. (It also contains the full Euler equation formula generating the results, for those who want the mathematical details.) We first estimate real rates under the baseline calibration above, before considering variations in the critical inputs.
Baseline results. The model predicts that under zero probability of transformative AI, the real rate at any horizon would be 2.8%. In comparison, under the baseline calibration just described based on Cotra timelines, the real rate at a 30-year horizon would be pushed up to 5.9% – roughly three percentage points higher.
For comparison, the 30-year real rate in the US is currently 1.6%.
While the simple Euler equation somewhat overpredicts the level of the real interest rate even under zero probability of transformative AI – the 2.8% in the model versus the 1.6% in the data – this overprediction is explainable by the radical simplicity of the model that we use and is a known issue in the literature. Adding other factors (e.g. precautionary savings) to the model would lower the level. Changing the level does not change its directional predictions, which help quantitatively explain the fall in real rates over the past ~30 years.
Therefore, what is most informative is the three percentage point difference between the real rate under Cotra timelines (5.9%) versus under no prospect of transformative AI (2.8%): Cotra timelines imply real interest rates substantially higher than their current levels.
Now, from this baseline estimate, we can also consider varying the key inputs.
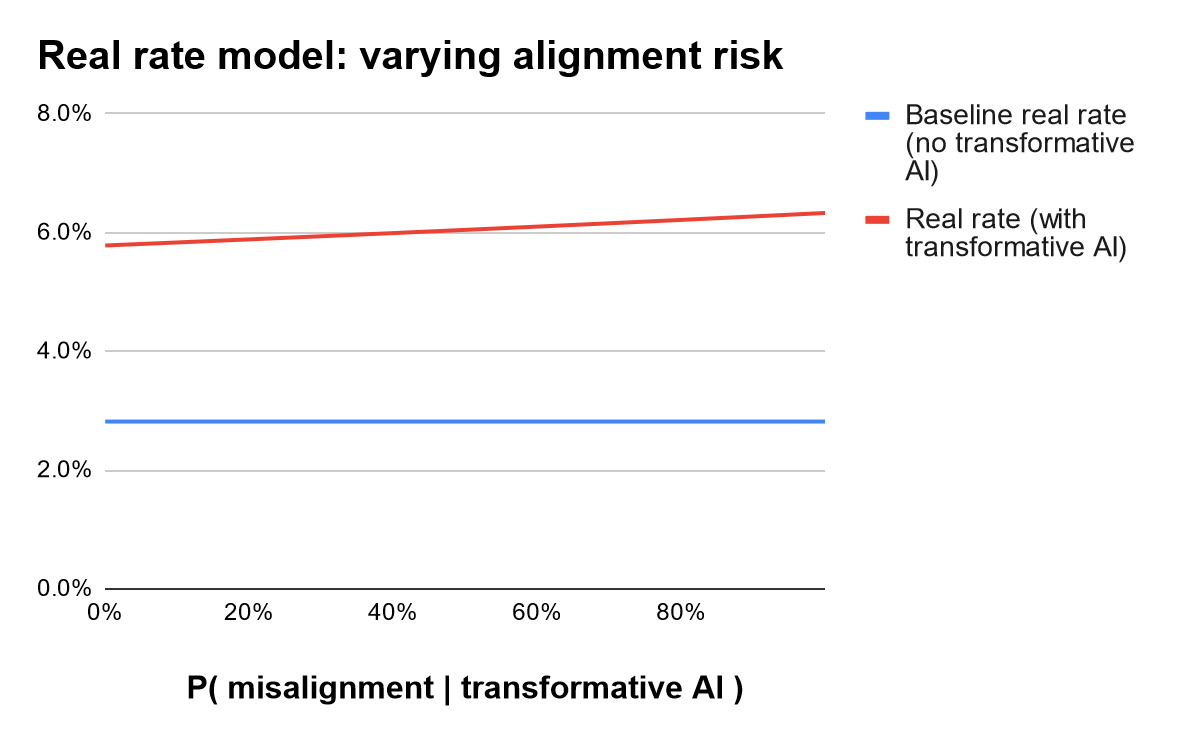
Varying assumptions on P(misaligned|AGI). First consider changing the assumption that advanced AI is 15% likely to be unaligned (conditional on the development of AGI). Varying this parameter does not have a large impact: moving from 0% to 100% probability of misalignment raises the model’s predicted real rate from 5.8% only to 6.3%.
Varying assumptions on timelines. Second, consider making timelines shorter or longer. In particular, consider varying the probability of development by 2043, which we use as a benchmark per the FTX Future Fund.
We scale the Cotra timelines up and down to vary the probability of development by 2043. (Specifically: we target a specific cumulative probability of development by 2043; and, following Cotra, if the annual probability up until 2030 is , then it is in the subsequent seven years up through 2036, and it is in the remaining years of the 30-year window.)
As the next figure shows and as one might expect, shorter AI timelines have a very large impact on the model’s estimate for the real rate.
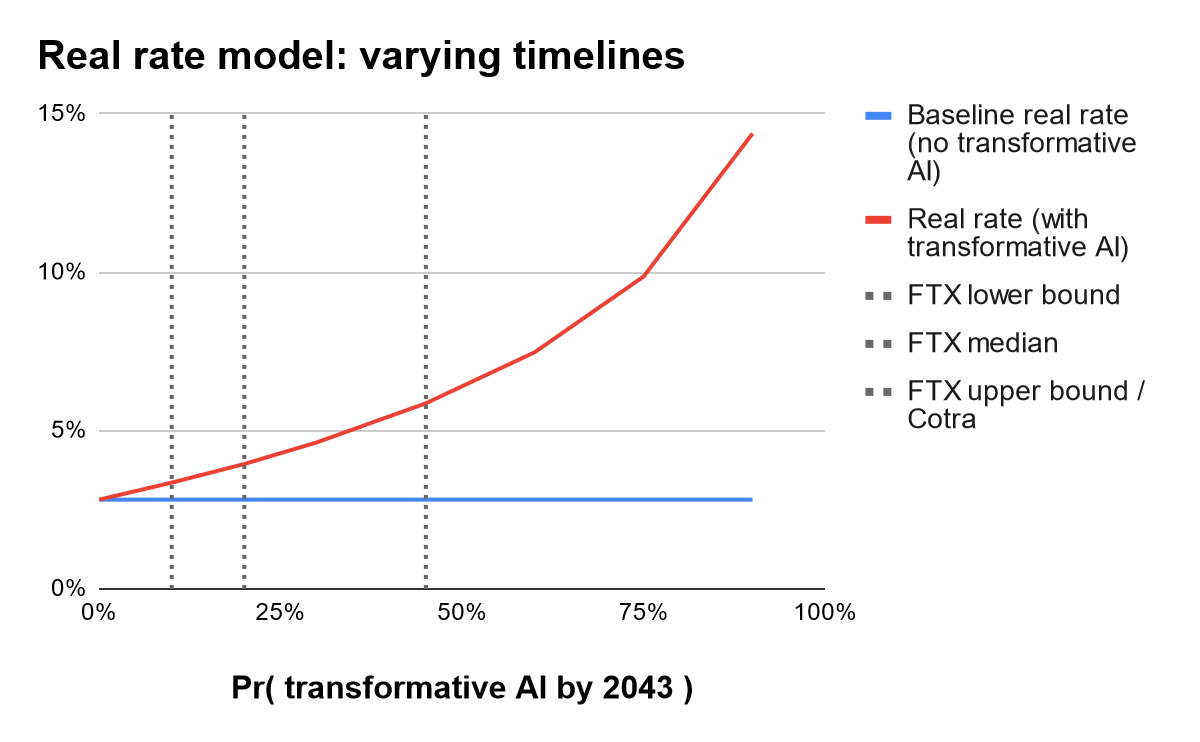
- The original baseline parameterization from Cotra corresponds to the FTX Future Fund “upper threshold” of a 45% chance of development by 2043, which generated the 3 percentage point increase in the 30-year real rate discussed above.
- The Future Fund’s median of a 20% probability by 2043 generates a 1.1 percentage point increase in the 30-year real rate.
- The Future Fund’s “lower threshold” of a 10% probability by 2043 generates a 0.5 percentage point increase in the real rate.
These results strongly suggest that any timeline shorter than or equal to the Cotra timeline is not being expected by financial markets.
VIII. Markets are decisively rejecting the shortest possible timelines
While it is not possible to back out exact numbers for the market’s implicit forecast for AI timelines, it is reasonable to say that the market is decisively rejecting – i.e., putting very low probability on – the development of transformative AI in the very near term, say within the next ten years.
Consider the following examples of extremely short timelines:
- Five year timelines: With a 50% probability of transformative AI by 2027, and the same yearly probability thereafter, the model predicts 13.0pp higher 30-year real rates today!
- Ten year timelines: With a 50% probability of transformative AI by 2032, and the same yearly probability thereafter, the model predicts 6.5pp higher 30-year real rates today.
Real rate movements of these magnitudes are wildly counterfactual. As previously noted, real rates in the data used above have never gone above even 5%.
Stagnation. As a robustness check, in the configurable spreadsheet we allow you to place some yearly probability on the economy stagnating and growing at 0% per year from thereon. Even with a 20% chance of stagnation by 2053 (higher than realistic), under Cotra timelines, the model generates a 2.1% increase in 30-year rates.
Recent market movements. Real rates have increased around two percentage points since the start of 2022, with the 30-year real rate moving from -0.4% to 1.6%, approximately the pre-covid level. This is a large enough move to merit discussion. While this rise in long-term real rates could reflect changing market expectations for timelines, it seems much more plausible that high inflation, the Russia-Ukraine war, and monetary policy tightening have together worked to drive up short-term real rates and the risk premium on long-term real rates.
IX. Financial markets are the most powerful information aggregators produced by the universe (so far)
Should we update on the fact that markets are not expecting very short timelines?
Probably!
As a prior, we think that market efficiency is reasonable. We do not try to provide a full defense of the efficient markets hypothesis (EMH) in this piece given that it has been debated ad nauseum elsewhere, but here is a scaffolding of what such an argument would look like.
Loosely, the EMH says that the current price of any security incorporates all public information about it, and as such, you should not expect to systematically make money by trading securities.
This is simply a no-arbitrage condition, and certainly no more radical than supply and demand: if something is over- or under-priced, you’ll take action based on that belief until you no longer believe it. In other words, you’ll buy and sell it until you think the price is right. Otherwise, there would be an unexploited opportunity for profit that was being left on the table, and there are no free lunches when the market is in equilibrium.
As a corollary, the current price of a security should be the best available risk-adjusted predictor of its future price. Notice we didn’t say that the price is equal to the “correct” fundamental value. In fact, the current price is almost certainly wrong. What we did say is that it is the best guess, i.e. no one knows if it should be higher or lower.
Testing this hypothesis is difficult, in the same way that testing any equilibrium condition is difficult. Not only is the equilibrium always changing, there is also a joint hypothesis problem which Fama (1970) outlined: comparing actual asset prices to “correct” theoretical asset prices means you are simultaneously testing whatever asset pricing model you choose, alongside the EMH.
In this sense, it makes no sense to talk about “testing” the EMH. Rather, the question is how quickly prices converge to the limit of market efficiency. In other words, how fast is information diffusion? Our position is that for most things, this is pretty fast!
Here are a few heuristics that support our position:
- For our purposes, the earlier evidence on the link between real rates and growth is a highly relevant example of market efficiency.
- There are notable examples of markets seeming to be eerily good at forecasting hard-to-anticipate events:
- In the wake of the Challenger explosion, despite no definitive public information being released, the market seems to have identified which firm was responsible.
- Economist Armen Alchian observed that the stock price of lithium producers spiked 461% following the public announcement of the first hydrogen bomb tests in 1954, while the prices of producers of other radioactive metals were flat. He circulated a paper within RAND, where he was working, identifying lithium as the material used in the tests, before the paper was suppressed by leadership who were apparently aware that indeed lithium was used. The market was prescient even though zero public information was released about lithium’s usage.
Remember: if real interest rates are wrong, all financial assets are mispriced. If real interest rates “should” rise three percentage points or more, that is easily hundreds of billions of dollars worth of revaluations. It is unlikely that sharp market participants are leaving billions of dollars on the table.
X. If markets are not efficient, you could be earning alpha and philanthropists could be borrowing
While our prior in favor of efficiency is fairly strong, the market could be currently failing to anticipate transformative AI, due to various limits to arbitrage.
However, if you do believe the market is currently wrong about the probability of short timelines, then we now argue there are two courses of action you should consider taking:
- Bet on real rates rising (“get rich or die trying”)
- Borrow today, including in order to fund philanthropy (“impatient philanthropy”)
1. Bet on real rates rising (“get rich or die trying”)
Under the logic argued above, if you genuinely believe that AI timelines are short, then you should consider putting your money where your mouth is: bet that real rates will rise when the market updates, and potentially earn a lot of money if markets correct. Shorting (or going underweight) government debt is the simplest way of expressing this view.
Indeed, AI safety researcher Paul Christiano has written publicly that he is (or was) short 30-year government bonds.
If short timelines are your true belief in your heart of hearts, and not merely a belief in a belief, then you should seriously consider how much money you could earn here and what you could do with those resources.
Implementing the trade. For retail investors, betting against treasuries via ETFs is perhaps simplest. Such trades can be done easily with retail brokers, like Schwab.
(i) For example, one could simply short the LTPZ ETF, which holds long-term real US government debt (effective duration: 20 years).
(ii) Alternatively, if you would prefer to avoid engaging in shorting yourself, there are ETFs which will do the shorting for you, with nominal bonds: TBF is an ETF which is short 20+ year treasuries (duration: 18 years); TBT is the same, but levered 2x; and TTT is the same, but levered 3x. There are a number of other similar options. Because these ETFs do the shorting for you, all you need to do is purchase shares of the ETFs.
Back of the envelope estimate. A rough estimate of how much money is on the table, just from shorting the US treasury bond market alone, suggests there is easily $1 trillion in value at stake from betting that rates will rise.
- In response to a 1 percentage point rise in interest rates, the price of a bond falls in percentage terms by its “duration”, to a first-order approximation.
- The average value-weighted duration of (privately-held) US treasuries is approximately 4 years.
- So, to a first-order approximation, if rates rise by 3 percentage points, then the value of treasuries will fall by 12% (that is, 3*4).
- The market cap of (privately-held) treasuries is approximately $17 trillion.
- Thus, if rates rise by 3 percentage points, then the total value of treasuries can be expected to fall by $2.04 trillion (that is, 12%*17 trillion).
- Slightly more than half (55%) of the interest rate sensitivity of the treasury market comes from bonds with maturity beyond 10 years. Assuming that the 3 percentage point rise occurs only at this horizon, and rounding down, we arrive at the $1 trillion estimate.
Alternatively, returning to the LTPZ ETF with its duration of 20 years, a 3 percentage point rise in rates would cause its value to fall by 60%. Using the 3x levered TTT with duration of 18 years, a 3 percentage point rise in rates would imply a mouth-watering cumulative return of 162%.
While fully fleshing out the trade analysis is beyond the scope of this post, this illustration gives an idea of how large the possibilities are.
The alternative to this order-of-magnitude estimate would be to build a complete bond pricing model to estimate more precisely the expected returns of shorting treasuries. This would need to take into account e.g. the convexity of price changes with interest rate movements, the varied maturities of outstanding bonds, and the different varieties of instruments issued by the Treasury. Further refinements would include trading derivatives (e.g. interest rate futures) instead of shorting bonds directly, for capital efficiency, and using leverage to increase expected returns.
Additionally, the analysis could be extended beyond the US government debt market, again since changes to real interest rates would plausibly impact the price of every asset: stocks, commodities, real estate, everything.
(If you would be interested in fully scoping out possible trades, we would be interested in talking.)
Trade risk and foom risk. We want to be clear that – unless you are risk neutral, or can borrow without penalty at the risk-free rate, or believe in short timelines with 100% probability – then such a bet would not be a free lunch: this is not an “arbitrage” in the technical sense of a risk-free profit. One risk is that the market moves in the other direction in the short term, before correcting, and that you are unable to roll over your position for liquidity reasons.
The other risk that could motivate not making this bet is the risk that the market – for some unspecified reason – never has a chance to correct, because (1) transformative AI ends up unaligned and (2) humanity’s conversion into paperclips occurs overnight. This would prevent the market from ever “waking up”.
However, to be clear, expecting this specific scenario requires both:
- Buying into specific stories about how takeoff will occur: specifically, Yudkowskian foom-type scenarios with fast takeoff.
- Having a lot of skepticism about the optimization forces pushing financial markets towards informational efficiency.
You should be sure that your beliefs are actually congruent with these requirements, if you want to refuse to bet that real rates will rise. Additionally, we will see that the second suggestion in this section (“impatient philanthropy”) is not affected by the possibility of foom scenarios.
2. Borrow today, including in order to fund philanthropy (“impatient philanthropy”)
If prevailing interest rates are lower than your subjective discount rate – which is the case if you think markets are underestimating prospects for transformative AI – then simple cost-benefit analysis says you should save less or even borrow today.
An illustrative example. As an extreme example to illustrate this argument, imagine that you think that there is a 50% chance that humanity will be extinct next year, and otherwise with certainty you will have the same income next year as you do this year. Suppose the market real interest rate is 0%. That means that if you borrow $10 today, then in expectation you only need to pay $5 off, since 50% of the time you expect to be dead.
It is only if the market real rate is 100% – so that your $10 loan requires paying back $20 next year, or exactly $10 in expectation – that you are indifferent about borrowing. If the market real rate is less than 100%, then you want to borrow. If interest rates are “too low” from your perspective, then on the margin this should encourage you to borrow, or at least save less.
Note that this logic is not affected by whether or not the market will “correct” and real rates will rise before everyone dies, unlike the logic above for trading.
Borrowing to fund philanthropy today. While you may want to borrow today simply to fund wild parties, a natural alternative is: borrow today, locking in “too low” interest rates, in order to fund philanthropy today. For example: to fund AI safety work.
We can call this strategy “impatient philanthropy”, in analogy to the concept of “patient philanthropy”.
This is not a call for philanthropists to radically rethink their cost-benefit analyses. Instead, we merely point out: ensure that your financial planning properly accounts for any difference between your discount rate and the market real rate at which you can borrow. You should not be using the market real rate to do your financial planning. If you have a higher effective discount rate due to your AI timelines, that could imply that you should be borrowing today to fund philanthropic work.
Relationship to impatient philanthropy. The logic here has a similar flavor to Phil Trammell’s “patient philanthropy” argument (Trammell 2021) – but with a sign flipped. Longtermist philanthropists with a zero discount rate, who live in a world with a positive real interest rate, should be willing to save all of their resources for a long time to earn that interest, rather than spending those resources today on philanthropic projects. Short-timeliners have a higher discount rate than the market, and therefore should be impatient philanthropists.
(The point here is not an exact analog to Trammell 2021, because the paper there considers strategic game theoretic considerations and also takes the real rate as exogenous; here, the considerations are not strategic and the endogeneity of the real rate is the critical point.)
XI. Conclusion: outside views vs. inside views & future work
We do not claim to have special technical insight into forecasting the likely timeline for the development of transformative artificial intelligence: we do not present an inside view on AI timelines.
However, we do think that market efficiency provides a powerful outside view for forecasting AI timelines and for making financial decisions. Based on prevailing real interest rates, the market seems to be strongly rejecting timelines of less than ten years, and does not seem to be placing particularly high odds on the development of transformative AI even 30-50 years from now.
We argue that market efficiency is a reasonable benchmark, and consequently, this forecast serves as a useful prior for AI timelines. If markets are wrong, on the other hand, then there is an enormous amount of money on the table from betting that real interest rates will rise. In either case, this market-based approach offers a useful framework: either for forecasting timelines, or for asset allocation.
Opportunities for future work. We could have put 1000 more hours into the empirical side or the model, but, TIABPNAJA. Future work we would be interested in collaborating on or seeing includes:
- More careful empirical analyses of the relationship between real rates and growth. In particular, (1) analysis of data samples with larger variation in growth rates (e.g. with the Industrial Revolution, China or the East Asian Tigers), where a credible measure of real interest rates can be used; and (2) causally identified estimates of the relationship between real rates and growth, rather than correlations. Measuring historical real rates is the key challenge, and the main reason why we have not tried to address these here.
- Any empirical analysis of how real rates vary with changing existential risk. Measuring changes in existential risk is the key challenge.
- Alternative quantitative models on the relationship between real interest rates and growth/x-risk with alternative preference specifications, incomplete markets, or disaster risk.
- Tests of market forecasting ability at longer time horizons for any outcome of significance; and comparisons of market efficiency at shorter versus longer time horizons.
- Creation of sufficiently-liquid genuine market instruments for directly measuring outcomes we care about like long-horizon GDP growth: e.g. GDP swaps, GDP-linked bonds, or binary GDP prediction markets. (We emphasize market instruments to distinguish from forecasting platforms like Metaculus or play-money sites like Manifold Markets where the forceful logic of financial market efficiency simply does not hold.)
- An analysis of the most capital-efficient way to bet on short AI timelines and the possible expected returns (“the greatest trade of all time”).
- Analysis of the informational content of infinitely-lived assets: e.g. the discount rates embedded in land prices and rental contracts. There is an existing literature related to this topic: [1], [2], [3], [4], [5], [6], [7].
- This literature estimates risky, nominal discount rates embedded in rental contracts out as far as 1000 years, and finds surprisingly low estimates – certainly less than 10%. This is potentially extremely useful information, though this literature is not without caveats. Among many other things, we cannot have the presumption of informational efficiency in land/rental markets, unlike financial markets, due to severe frictions in these markets (e.g. inability to short sell).
Thanks especially to Leopold Aschenbrenner, Nathan Barnard, Jackson Barkstrom, Joel Becker, Daniele Caratelli, James Chartouni, Tamay Besiroglu, Joel Flynn, James Howe, Chris Hyland, Stephen Malina, Peter McLaughlin, Jackson Mejia, Laura Nicolae, Sam Lazarus, Elliot Lehrer, Jett Pettus, Pradyumna Prasad, Tejas Subramaniam, Karthik Tadepalli, Phil Trammell, and participants at ETGP 2022 for very useful conversations on this topic and/or feedback on drafts.
Update 1: we have now posted a comment summarising our responses to the feedback we have received so far.
Postscript
OpenAI’s ChatGPT model on what will happen to real rates if transformative AI is developed:

🤔🤔🤔🤔🤔🤔🤔🤔🤔🤔🤔🤔🤔🤔🤔🤔🤔🤔🤔🤔🤔🤔🤔🤔🤔🤔
Some framings you can use to interpret this post:
- “This blog post takes Fama seriously” [a la Mankiw-Romer-Weil]
- “The market-clearing price does not hate you nor does it love you” [a la Yudkowsky]
- “Existential risk and asset pricing” [a la Aschenbrenner 2020, Trammell 2021]
- “Get rich or hopefully don’t die trying” [a la 50 Cent]
- “You can short the apocalypse.” [contra Peter Thiel, cf Alex Tabarrok]
- “Tired: market monetarism. Inspired: market longtermism.” [a la Scott Sumner]
- “This is not not financial advice.” [a la the standard disclaimer]
Appendix 1. Against using stock prices to forecast AI timelines
Link to separate EA Forum post







Trying again:
OP seems to ambiguate between two ideas, one true idea, and one false idea.
The true idea is that if Omega tells you personally that the world will end in 2030 with probability 1, you personally should not bother saving for retirement. Call this the Personal Idea.
The false idea is that if you believe in foomdoom, you should go long real interest rates and expect a market profit. Call this the Market Idea.
Intuitively, at least if you're swayed by this essay, the idea in Market probably seems pretty close to the idea in Personal. If everybody started consuming for today and investing less, real interest rates would go up, right? So if you don't believe that Market is about as strong as Personal, what invalid reasoning step occurs within the gap between the true premise in Personal to the false conclusion in Market?
Is it invalid that if in 2025 everyone started believing that the world would end in 2030 with probability 1, real interest rates would rise in 2025? Honestly, I'm not even sure of that in real life. People are arguing clever-ideas like 'Shouldn't everyone take out big loans due later?' but maybe the lender doesn't want to lend anymore, if everyone knows that. There's a supply collapse and a demand collapse and yes I see the theoretical argument but real-world monetary stuff is in fact really strange and complicated; I didn't see anybody calling the actual interest-rate trajectory surrounding Covid in advance of it actually playing out.
In real life, what zaps you when you think there's a worldwide pandemic coming and try to trade interest rates, isn't that you didn't know about the pandemic ahead of the oblivious market, it's that you guessed wrong about what the market would really actually do in real life as the pandemic played out and finally ended.
You can sometimes make a profit off an oblivious market, if you guess narrowly enough at reactions that are much more strongly determined. Wei Dai reports making huge profits on the Covid trade against the oblivious market there, after correctly guessing that people soon noticing Covid would at least increase expected volatility and the price of downside put options would go up.
But I don't think anybody called "there will be a huge market drop followed by an even steeper market ascent, after the Fed's delayed reaction to a huge drop in TIPS-predicted inflation, and people staying home and saving and trading stocks, followed by skyrocketing inflation later."
I don't think the style of reasoning used in the OP is the kind of thing that works reliably. It's doing the equivalent of trying to predict something harder than 'once the pandemic really hits, people in the short term will notice and expect more volatility and option prices will go up'; it's trying to do the equivalent of predicting the market reaction to the Fed reaction a couple of years later.
The entire OP is written as if we lived in an alternate universe where it is way way easier than history has actually shown, to figure out what happens in broad markets after any sort of complicated or nontrivial event occurs in real life that isn't on the order of "unexpected Fed rate hike" or "company reports much higher-than-expected profits". And it's written in such a way as to mislead EAs reading it about the general confidence that the field of economics is able to justly put in predictions about broad market reactions to strange things.
If you haven't already looked at OP's recommended investment instrument of (short) LPTZ, which holds inflation-protected Treasuries and is therefore their recommended way of tracking real interest rates, I recommend the following exercise: First try to figure out what you would have believed a priori, without benefit of hindsight, real interest rates would do over the course of a pandemic. Then, decide what investment strategy you'd have followed with LTPZ if you thought you knew about a pandemic ahead of the market. Then, decide what you think happened to real interest rates with benefit of hindsight. Then, go look at the actual price trajectory of their recommended instrument of LTPZ.
I am not sure I can properly convey this thought that I am trying to convey; I have had trouble actually conveying this thought to EAs before. The thought is that people often do long careful serious-sounding writeups which EAs then take Very Seriously, because they are so long and so seriously argued, but in fact fail to bind to reality entirely, in a way that doesn't have to do with the details of the complicated arguments. Very serious arguments about what ought to happen to the price of an ETF that tracks 15-year TIPS, via the intermediate step of arguing about what logically ought to happen to real interest rates, are the sort of thing that, historically, average economists have not really been able to pull off; it's a kind of thought that you should expect fails to achieve basic binding to reality. What would LTPZ or its post-facto equivalent have been doing around the time of the Cuban Missile Crisis? My model says 'no prediction'; they'll have done whatever. Afterwards somebody will make up a story about it in hindsight, but it is not the sort of thing where history says that long complicated analyses are remotely reliably good at doing it in advance.
But there are even weaker links in the argument, so let's accept the LTPZ step arguendo and pass on.
An even bigger problem is that, since everybody is going to die before anything really pays out, the marginal foresightful trader does not have a strong incentive to early-on move the market toward where the market would end up in equilibrium after everyone agreed on the actual facts of the matter and had time to trade about them.
Prediction markets, I sometimes explain to people, are tools for transmitting future observables, or more generally propositions that people expect to publicly agree on at some future point even if they don't agree now, lossily backward in time, manifesting as well-calibrated probability distributions.
To run a prediction market, you first and foremost need a future publicly observable measurement, which is a special case of a place where we expect most people to agree on an extreme probability assignment later, even though they don't agree now or don't make extreme probability assignments now. You cannot run a prediction market on whether supplementing lots of potassium can produce weight loss; you can only run a prediction market about what an experiment will report in the way of results, or what a particular judge will say the experimental evidence seems to have indicated in five years. You cannot directly observe "whether potassium causes weight loss" as an underlying fact of biology, so you can't have a prediction market about that; you can only observe what somebody reports as an experimental result, or what a particular person appointed as judge says out loud about the state of evidence later.
The marginal foresightful trader usually has a motive to run ahead of the market and make trades now, based on where the equilibrium ought to settle later; not because they are nobly undertaking a grand altruistic project of transmitting facts backward in time and making the market behave nicely from the standpoint of theoretical economics, but because they expect to get paid after everyone makes the common observation and the market settles into a new equilibrium reflecting that state of knowledge. And then they expect to have that money, or to get a bonus for earning that money for their proprietary trading firm, and for that money to still hold its value, and for them to be able to spend the money on nice things.
In the unusual case of foomdoom, even if doom proceeds slowly enough that a large-enough group of marginal foresightful traders see the foomdoom coming, even if there is somehow a really definitive fire alarm that says "extremely high probability you are dead within two to four years", it is incredibly unlikely that everyone in the world will agree that yes we'll all be dead in two to four years, and that the markets will settle into the equilibrium that an economist would say corresponds to the belief that we'll all be dead in two to four years; which is what's required for the foresightful proprietary trader to score a huge profit and get a big bonus that year and have time to spend it on some fancy way of passing the remaining time.
People do not usually agree on what will happen in two to four years. This kind of agreement that reliably reflects a fact, and makes a market pay out in a way that you can trust to correspond to that fact, is usually achieved after that fact is publicly definitively observed, not two to four years ahead of the observation.
In case of foomdoom the world never settles into equilibrium later, the bets never pay out, there is never that moment where everybody says "What a foresightful trader that was!" and agree on the fact that yes we sure are all dead now. So even if a proprietary trader sees doom coming, they do not have much of an incentive to dutifully transmit that information backward in time in order to make the market behave now in the way that an economist thinks ought to correspond to the equilibrium it would settle into after everybody agreed that they were dead.
That incentive would only exist if you expected everybody to agree that they were going to die in a few years, far enough ahead of everybody actually being dead, for the markets to settle into equilibrium and foresightful traders to collect bonuses on having made the trade before that. Which is a much stronger and stranger thing to claim, about a planet like Earth, than the usual much weaker claim that a few sharp traders might see a fact coming, and move the markets a few years ahead of time to where they would go after everybody agreed on that fact later.
Though even then, of course, we have cases like the financial crisis of 2006-2008, where some traders did see it coming and turn huge profits, but couldn't move enough marginal money around to actually shift the entire broader market.
To suppose that the market is broken around foomdoom is really not a remotely surprising market behavior to suppose! Even in a world where nearly all the prices are efficient relative to you and that's why you can't make 10%/day trading Microsoft stock!
What happened in 2006-2008 was much more broken than that! Marginal traders saw it coming, and some of them won huge even though CDSs were not trivial to short; but they didn't move enough money to shift anything remotely as large as 'real interest rates' ahead of the actual materialization of the disaster.
The market's behavior around Covid also showed much more obliviousness than this; it showed the kind of obliviousness where people I'd previously marked as the strongest EMH challengers reported collecting vast profits over a timespan of a couple of months. (But on chains of logic much less fraught than OP's, because in real life you can't call LTPZ movements or real interest rate changes in advance, just things on the order of 'buy volatility'.)
We should not believe 'the market', in the sense of that unusually intelligent entity whose opinions we actually pay attention to, driven by the highly incentivized marginal trader, has any opinion on AGI except that "in the next few years, not everyone will have started believing that they are going to die in a few years after that". The market is showing no actual opinion on foomdoom, only on what most market participants will believe about foomdoom in a couple of years. The usual incentive mechanism whereby, if a pandemic starts, in a few years most market participants will agree that this pandemic happened and foresightful traders will collect bonuses and spend them - as is responsible for the market sometimes but not always being foresightful, because it is paid to be foresightful - is in this case broken. We are really always seeing, when the market foretells an observable's value a few years later, that the foresightful marginal trader thinks that a few years later lots of people will hold a certain opinion; it's just that usually, this common opinion is being mundanely driven by a direct observation.
The market says, "It won't be the case that in 2030, everyone agrees that they were killed by AGIs." The market isn't saying anything about whether that's because everyone agrees they are alive, or because nobody is left to agree anything.
OP reads like somebody has heard that markets sometimes anticipate things ahead of them happening, that markets sometimes transmit information lossily backward in time, and doesn't quite seem to have understood the mechanism behind it; that what everyone will agree on later, unusually foresightful marginal traders can sometimes cause the market to reflect now even though not everyone agrees on it yet. Instead they are talking about "What if the market believed..." as if this kind of market belief reflected a numerical majority of the people in the market believing that foomdoom would kill us all before 30-year bonds paid out. But this is not where the market gets its power to say things that we ought to pay special attention to (though even then market isn't always right about those things, or even righter than us, especially if those things are a little strange, eg Covid etc). The market gets its power from unusually foresightful marginal traders expecting to get a payoff from what everyone believes later after the thing actually happened and therefore most market participants agree about what happened. And this transmission mechanism is broken w/r/t AGI doom in a way that it wouldn't even be broken for an asteroid strike; with an asteroid strike, you might get weird effects from money losing its value in the future, but at least people could all agree on the asteroid strike coming. With AGI, I think you'd have to be pretty naive to expect everybody to agree that AGI will kill us in two years, two years before AGI kills us. So it is inappropriate to skip over a step we can usually skip over, and compress the true proposition "The market doesn't believe that everyone in 2030 will believe that in 2030 everyone is dead", to the false proposition "The market doesn't believe that in 2030 everyone will be dead."
Though again - also just to be clear - AGI ruin is a harder call than Covid and I wouldn't strongly expect the market to get it right, even if transmission weren't broken; and even if I thought the market would get it right after seeing GPT-4 and that transmission wasn't broken, I wouldn't buy "short LTPZ" as a surefire way to profit.